笛卡尔树

简介

首先我们看到这个序列 \([9,4,10,1,7,2,3]\)，现在我们找到它的最大值 \(10\)，并从中间劈开，此时分为了两个序列 \([9,4]\) 和 \([1,7,2,3]\)，接着对这两个序列继续这样的操作。

现在，将劈开后序列最大值和被劈开的数建立父子关系，于是便建立了这个树：

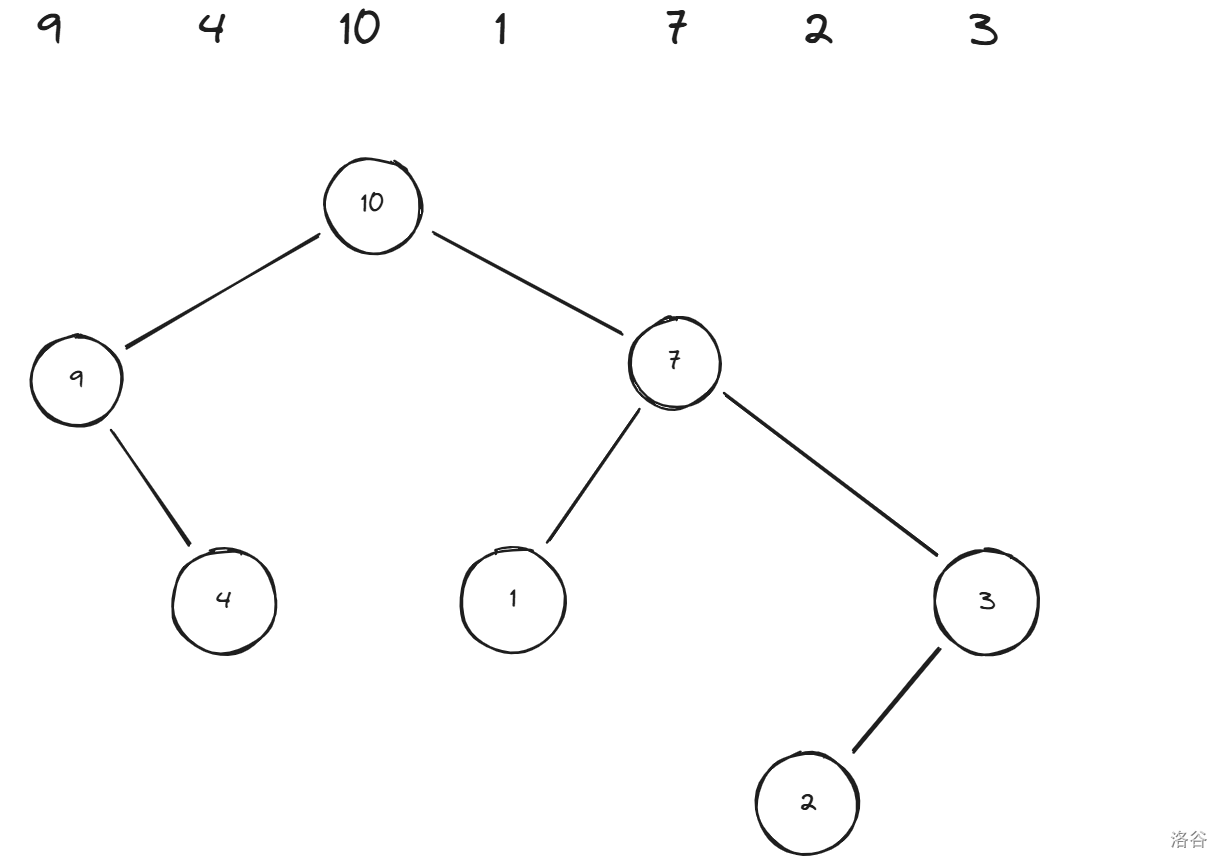
这也就是笛卡尔树。笛卡尔树满足堆，二叉搜索树的性质。

但是怎么建出这个树呢？

我们先看一下把这些结点连向其左右第一个比它大的结点的效果：

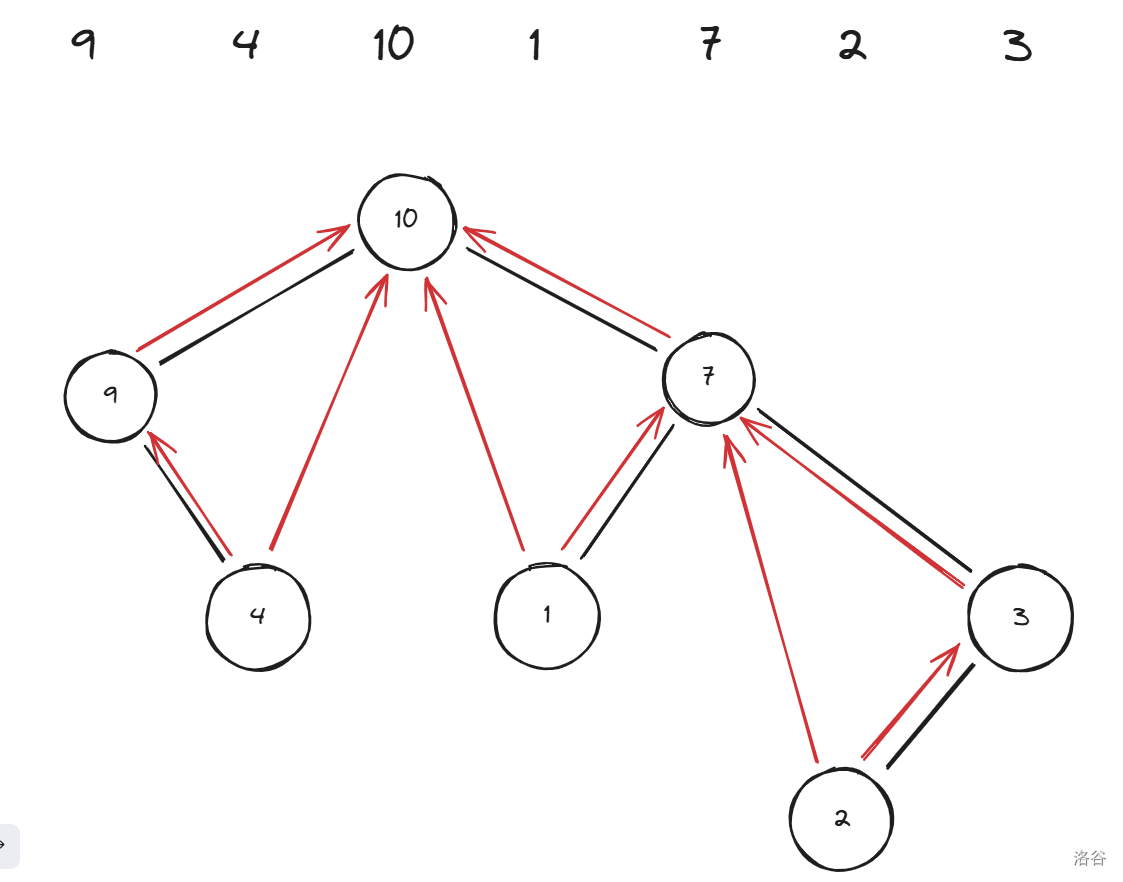
可以发现它的父亲刚好是其中较小的一个。证明也很简单，首先其父亲不可能小于它，其次，父亲一定是左右两边第一个比它大的数，如果不是那样，就只有可能是先选择离自己更远的数，再选择自己，但是还有比自己更大的数，矛盾。最后，父亲一定是较小的那个，因为较大的那个肯定更先选择，所以较小的才是父亲。用单调栈即可。

但是怎么快速求出一个点的左儿子和右儿子呢？

可以观察单调栈：当压入 \(x\) 时弹出的最后一个数，就是在 \(x\) 左边 \(<x\) 最大且最近的数，这不就是左儿子吗？再看 \(x\) 被弹出前的右边，也就是在 \(x\) 右边 \(<x\) 最大且最近的数，这也刚好就是右儿子。

应用

笛卡尔树可以用于求解一个区间极值为 \(x\) 的信息。比如以下这个最简单的问题：

给定一个柱状图，每个柱子的宽为 \(1\)，高为 \(a_i\)，求在该图中最大的一个矩形面积。

我们先来看下面这张图：

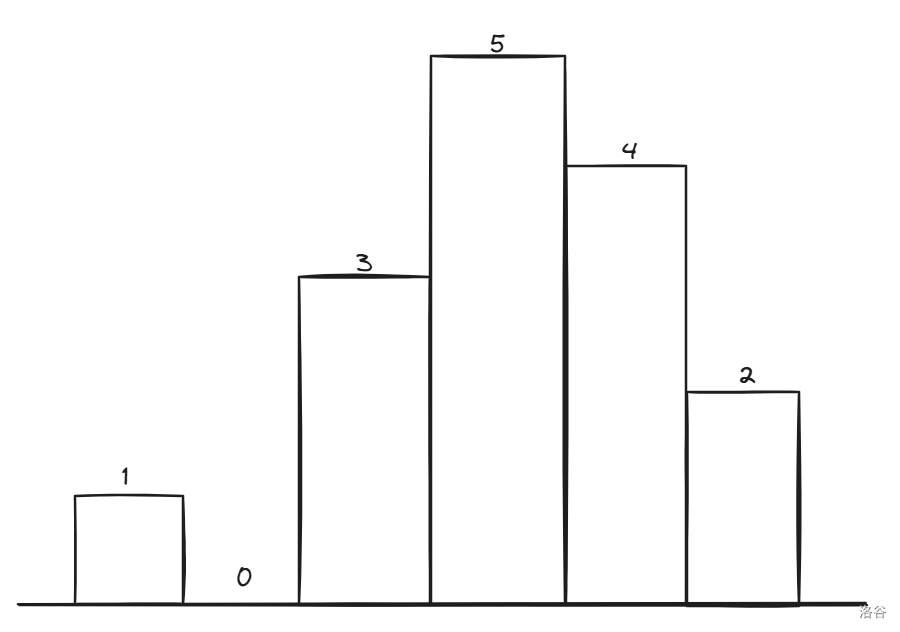
我们知道选择一个区间 \([l,r]\) 矩形面积最大值为 \(\min \limits_{i=l}^r \{a_i\}\cdot(r-l+1)\)。我们可以先枚举最小值，然后再来看最大能取多大的区间。

我们可以先建起一个小根笛卡尔树。可以发现笛卡尔树中 \(x\)（所选最小值）的子树就是 \(\ge x\) 的最大区间。所以只需枚举 \(x\)，最终求 \(\max \limits_{i=1}^N \{ a_i \cdot sz+i \}\) 即可（这里 \(sz_i\) 是 \(i\) 子树的大小）。