逐月信息学 2024 提高组 #1

\(\color{black} \texttt{A. 镜面反射}\)

题目描述

有一个未知的多边形，已知有两条对称轴的夹角为 \(\alpha ^\circ=\frac{p}{q}(0^\circ<\alpha ^\circ \le 90 ^\circ)\) ，求至少还有多少条对称轴。有 \(T(1\le T\le 10^5)\) 组询问。

思路

首先看下图：

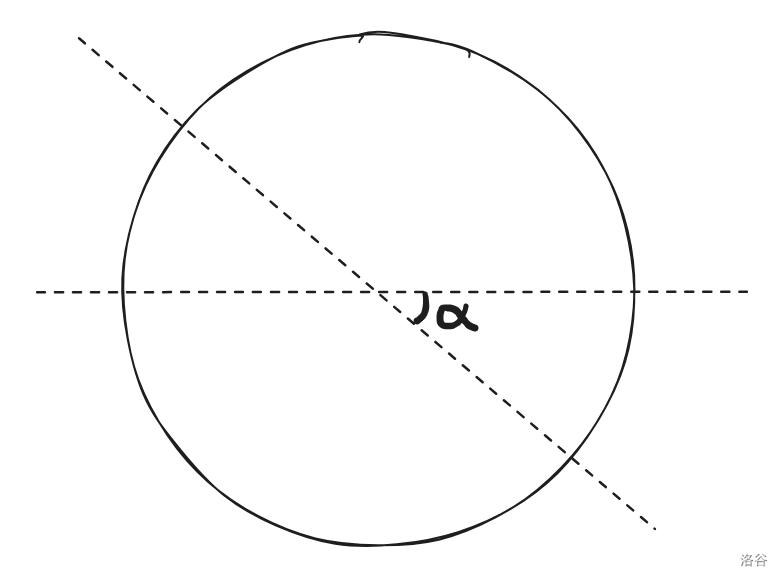
我们可以以横着的那条对称轴，把斜着的对称轴对称一下：

接着继续对称下去：

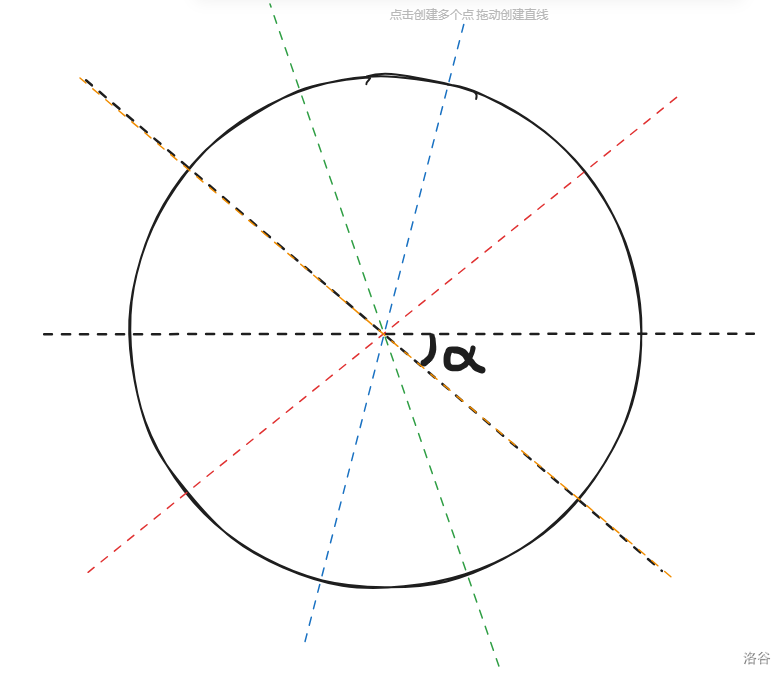
可以发现，这时两条对称轴重合了。所以继续对称下去就不会再得到新的对称轴了。

现在我们来推一推总共有多少条对称轴：

\[\begin{array}{l} \ \ \ \operatorname{lcm}(180, \frac{p}{q}) \div \frac{p}{q}\\ = 180 \times \frac{p}{q} \div \gcd(180, \frac{p}{q}) \times \frac{q}{p}\\ = 180 \div \frac{\gcd(180, p)}{\operatorname{lcm}(1, q)}\\ =180 \times q \div \gcd(180, p) \end{array} \]

这里，我们需要说明一下分数的 \(\gcd\)，实际上可以把除以 \(x\) 看作乘以 \(x^{-1}\)，这样就意味着分母不是做 \(\gcd\) 而是做 \(\operatorname{lcm}\)。

空间复杂度 \(O(1)\)，时间复杂度 \(O(T \log \max\{p,q\})\)。

代码

#include<bits/stdc++.h>
using namespace std;

int t, p, q;

int gcd(int a, int b) {
  return (!b ? a : gcd(b, a % b));
}

void Solve() {
  cin >> p >> q;
  int g = gcd(p, q);
  p /= g, q /= g;
  cout << 180ll * q / gcd(180, p) - 2 << "\n";
}

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  for(cin >> t; t--; Solve()) {
  }
  return 0;
}

总结

数学题，需要一定的思考。最后记得开 long long，以及答案 \(-2\) 和化简 \(\frac{p}{q}\)。

\(\color{black}\texttt{B. 九九乘法表}\)

递推水题，不讲。

\(\color{black}\texttt{C. 树上小游戏}\)

题目描述

有一棵 \(N = 2^k\) 个结点的满二叉树，树上每个点要么是黑色要么是白色。\(\texttt{Alice}\) 和 \(\texttt{Bob}\) 轮流进行操作，\(\texttt{Alice}\) 先手。每轮操作有三种选择：

• 将树上所有棋子移动到其左儿子上。若没有儿子则移出该棋子。
• 将树上所有棋子移动到其右儿子上。若没有儿子则移出该棋子。
• 将树上所有棋子复制成两个，分别移动到左右儿子上。若没有儿子则移出该棋子。

当所有棋子均被移出则游戏结束。若总共有偶数个黑色结点被棋子访问过，则 \(\texttt{Alice}\) 获胜。否则 \(\texttt{Bob}\) 获胜。

思路

首先我们先把二叉树改成三叉树，其中第三个儿子是把左右儿子权值相加的结果。然后在树上做 dp:

状态：\(dp_{u,0/1}\) 表示在子树 \(u\) 内是否可能使答案为奇数或偶数。
转移：$dp_{u,0}=\operatorname{op} \limits_{v\in S}\operatorname{not} dp_{v,c_u \operatorname{xor} 1} $，其中 \(S\) 表示 \(u\) 的儿子， \(c_u\) 表示 \(u\) 的颜色（\(1\) 为黑 \(0\) 为白）。

空间复杂度 \(O(3^{\log N})\)，时间复杂度 \(O(3^{\log N})\)。

代码

#include<bits/stdc++.h>
using namespace std;

const int MAXN = 15000000, MAXV = 16;

struct Node {
  int l, m, r, c;
}s[MAXN];

int n, m, in[MAXN], ROOT;
bool dp[MAXN][2];
vector<int> v[MAXV];

void DFS(int u, int x, int y) {
  s[u].c = (s[x].c ^ s[y].c);
  if(!s[x].l) {
    return;
  }
  s[u].l = ++n;
  DFS(n, s[x].l, s[y].l);
  s[u].r = ++n;
  DFS(n, s[x].r, s[y].r);
  s[u].m = ++n;
  DFS(n, s[u].l, s[u].r);
}

void dfs(int u) {
  if(!s[u].l) {
    return;
  }
  dfs(s[u].l), dfs(s[u].r);
  s[u].m = ++n;
  DFS(n, s[u].l, s[u].r);
}

void Dfs(int u) {
  if(!s[u].l) {
    dp[u][s[u].c] = 1;
    return;
  }
  Dfs(s[u].l);
  dp[u][0] |= !dp[s[u].l][s[u].c ^ 1];
  dp[u][1] |= !dp[s[u].l][s[u].c];
  Dfs(s[u].r);
  dp[u][0] |= !dp[s[u].r][s[u].c ^ 1];
  dp[u][1] |= !dp[s[u].r][s[u].c];
  Dfs(s[u].m);
  dp[u][0] |= !dp[s[u].m][s[u].c ^ 1];
  dp[u][1] |= !dp[s[u].m][s[u].c];
}

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n;
  m = n;
  for(int i = 1; i <= n; ++i) {
    cin >> s[i].l >> s[i].r >> s[i].c;
    in[s[i].l]++, in[s[i].r]++;
  }
  for(int i = 1; i <= n; ++i) {
    if(!in[i]) {
      ROOT = i;
      break;
    }
  }
  dfs(ROOT), Dfs(ROOT);
  for(int i = 1; i <= m; ++i) {
    cout << (dp[i][0] ? "Alice\n" : "Bob\n");
  }
  return 0;
}

总结

虽然很简单，但考场上没想到。

\(\color{black} \texttt{D. 签到}\)

题目描述

定义排列 \(a\) 和排列 \(b\)，\(a\circ b=[a_{b_1},a_{b_2},\dots,a_{b_n}],a^1=a,a^2=a\circ a,a^3=a\circ a\circ a,\dots ,a^k=\underbrace{a\circ a \circ \dots \circ a}_ k\)。现在给定长度为 \(N(1\le N \le 10^6)\) 的排列 \(A\) 和整数 \(M(1 \le M \le 10^{10^6})\)，求 \(A^M\)。

思路

这一道题很明显就是找环，然后计算循环节。可是问题在于 \(M\) 太大了，取模会炸掉。所以要用压位高精处理，以及记忆化。

空间复杂度 \(O(\log_{10} M)\)，时间复杂度 \(O(\sqrt N \frac{\log_{10} M}{18})\)。

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
using ll = long long;

const int MAXN = 1000005;
const ll _1e18 = (ll)(1e18);

int n, a[MAXN], cnt, tot, color, ans[MAXN], dp[MAXN];
bool vis[MAXN];
ll m[MAXN], x, abc;
vector<int> v[MAXN];

void dfs(int u) {
  if(vis[u]) {
    return;
  }
  vis[u] = 1, v[color].push_back(u);
  dfs(a[u]);
}

int Get(int MOD) {
  if(dp[MOD] != -1) {
    return dp[MOD];
  }
  int res = 0;
  for(int i = 1; i < tot; ++i) {
    res = (_1e18 % MOD * (ll)res % MOD + m[i] % MOD) % MOD;
  }
  res = (abc % MOD * res % MOD + m[tot] % MOD) % MOD;
  return dp[MOD] = res;
}

signed main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n;
  for(int i = 1; i <= n; ++i) {
    cin >> a[i];
  }
  char c;
  while(cin >> c) {
    x = 10ll * x + char(c - '0');
    if((++cnt) == 18) {
      m[++tot] = x, x = cnt = 0;
    }
  }
  abc = _1e18;
  if(x) {
    m[++tot] = x;
    abc = 1;
    for(int i = 1; i <= cnt; i++){
      abc *= 10ll;
    }
  }
  for(int i = 1; i <= n; ++i) {
    dp[i] = -1;
  }
  for(int i = 1; i <= n; ++i) {
    if(!vis[i]) {
      color++;
      dfs(i);
      int z = Get(v[color].size());
      for(int j = 0; j < (int)(v[color].size()); ++j) {
        ans[v[color][j]] = v[color][(j + z) % (int)(v[color].size())];
      }
    }
  }
  for(int i = 1; i <= n; ++i) {
    cout << ans[i] << " ";
  }
  return 0;
}