强连通分量、缩点

强连通分量

定义：强连通分量是指一个任意两点都可互相到达的极大子图。

求解思路和桥、割点和边双连通分量很类似。

首先跑出一颗dfs树，令 \(dfn_u\) 表示 \(u\) 的时间戳，\(low_u\) 表示 \(u\) 的子树中仅通过非树边能到达的 \(\min \{dfn_v\}\)。

比如下图：

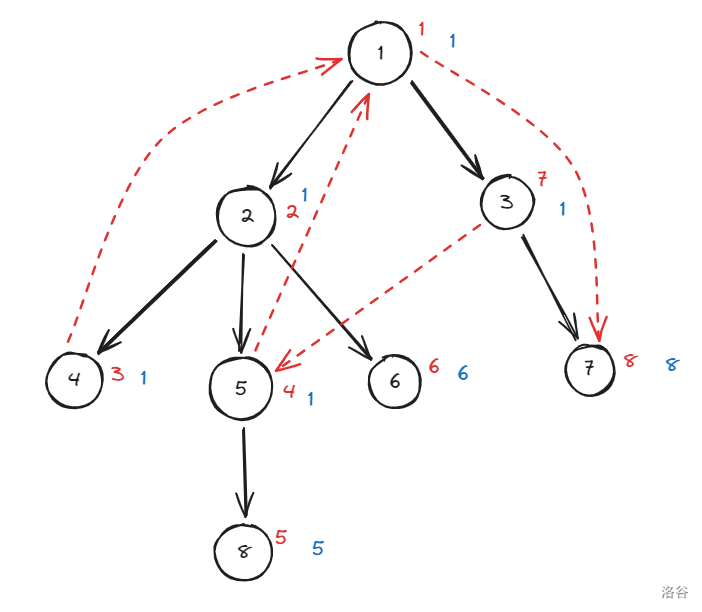
在这张图中，黑色边为树边，红色边为非树边，黑色数字表示编号，红色表示 \(dfn\)，蓝色数字表示 \(low\)。

这些点是强连通分量：

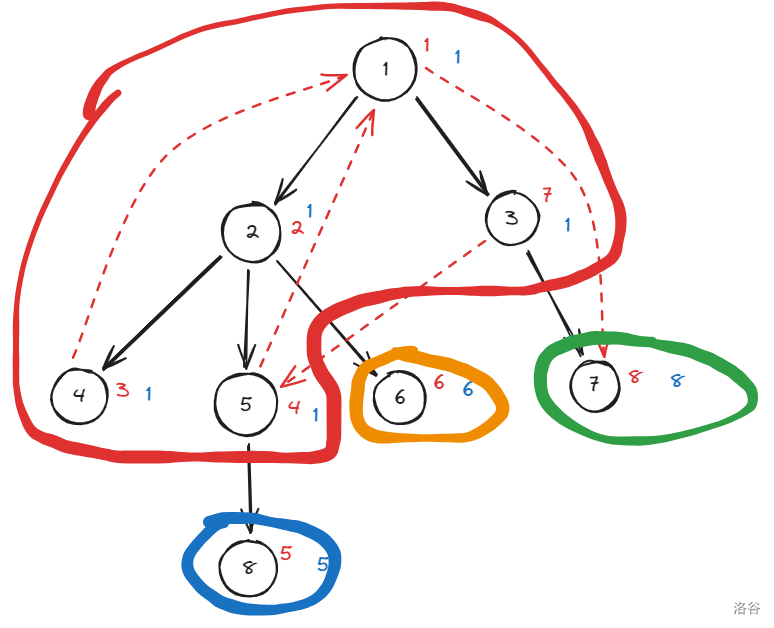
可以发现，所有强连通分量中 \(dfn\) 最小的结点一定 \(dfn_u=low_u\)，实际上这也很容易理解，如果自己子树中没有通向自己祖先的边，则代表这一部分是独立的。

所以我们可以开一个栈，栈中按dfs序记录结点。如果发现了一个结点的 \(dfn_u=low_u\)，则不断弹出栈顶直到弹出 \(u\)，弹出的结点就是一个强连通分量。

可是该怎么求解 \(low_u\) 呢？

根据定义，我们可以这样求：

设树上有一对条边 \(u\rightarrow v\)，

• 若 \(u\rightarrow v\) 的边是树边，则更新 \(low_u \leftarrow \min (low_u,low_v)\)。
• 若 \(u\rightarrow v\) 的边不是树边且 \(v\) 不在另一个强连通分量，则更新 \(low_u\leftarrow\min(low_u,dfn_v)\)。
• 否则，什么也不做。

代码

#include<bits/stdc++.h>
using namespace std;

const int MAXN = 500001, MAXM = 2000001;

int n, m, dfn[MAXN], low[MAXN], tot, stk[MAXN], top, color, col[MAXN];
vector<int> e[MAXN];

void dfs(int u, int fa) {
  dfn[u] = low[u] = ++tot, stk[++top] = u;
  for(int v : e[u]) {
    if(!dfn[v]) {
      dfs(v, u);
      low[u] = min(low[u], low[v]);
    }else if(!col[v]) {
      low[u] = min(low[u], dfn[v]);
    }
  }
  if(low[u] == dfn[u]) {
    color++;
    for(; dfn[stk[top]] >= dfn[u]; col[stk[top--]] = color) {
    }
  }
}

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n >> m;
  for(int i = 1, u, v; i <= m; ++i) {
    cin >> u >> v;
    e[u].push_back(v);
  }
  for(int i = 1; i <= n; ++i) {
    if(!dfn[i]) {
      dfs(i, 0);
    }
  }
  cout << color << "\n";
  for(int i = 1; i <= n; ++i) {
    cout << col[i] << " ";
  }
  return 0;
}