线段树

简介

线段树是一种 \(O(N)\) 建树，\(O(\log N)\) 区间查询区间修改的数据结构。线段树的思想就是把一个区间分成左右两半处理。线段树会将一个区间视作一个点，一个点的左儿子为左半区间，右儿子为右半区间。一般情况下，若一个点编号为 \(i\)，则其左右儿子编号分别为 \(2i,2i+1\)。

举个例子。当 \(A=\{3,1,4,1,5,9,2,6\}\)，并维护最大值时线段树如下：

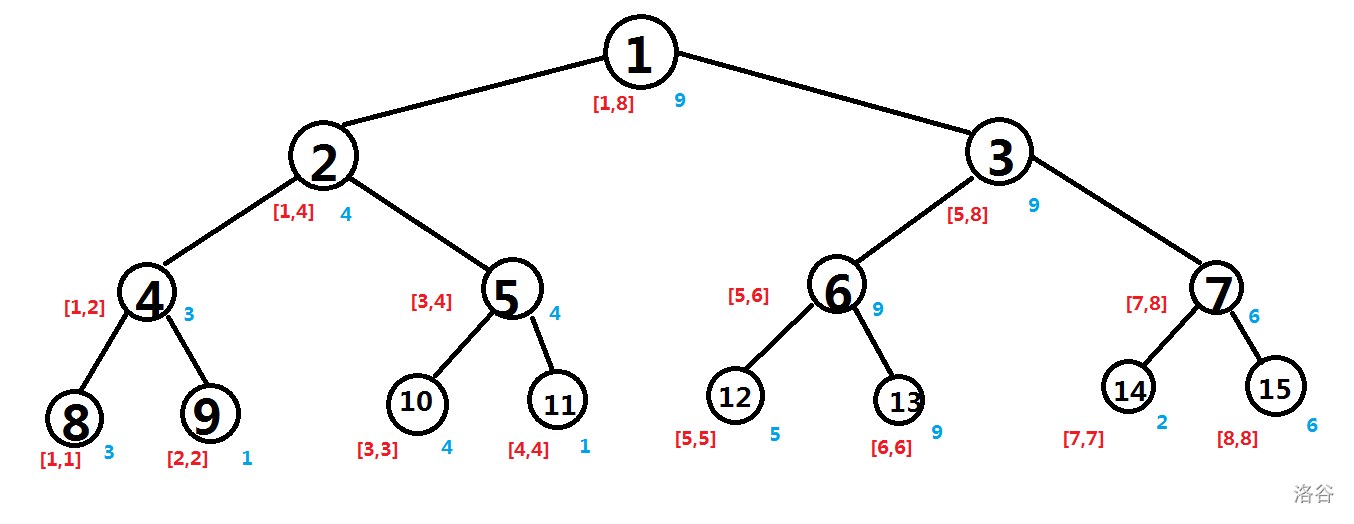
其中黑色数字代表编号，红色代表区间，蓝色代表值。

建树

使用递归求出每个节点的值即可。

由于每个节点都经过了一遍，所以时间复杂度为 \(N+\lfloor\frac{N}{2}\rfloor+\lfloor\frac{N}{4}\rfloor + \dots \le 2N = O(N)\)。

可是还有一个问题，空间该开多大呢？可以发现，当 \(N=2^x(x \ge 0)\) 时，节点编号最大会到达 \(2N-1\)，而如果不满足时，编号最大值与 \(2^{\lceil \log N \rceil}\) 时的最大值相同。所以空间就为 \(2^{\lceil \log N \rceil + 1}\)，而这个值可以近似为 \(4N\)，空间复杂度 \(O(N)\)。

代码

void build(int u, int l, int r) {
  if(l == r) {
    Max[u] = a[l];
    return;
  }
  int mid = (l + r) >> 1;
  build(2 * u, l, mid), build(2 * u + 1, mid + 1, r);
  Max[u] = max(Max[2 * u], Max[2 * u + 1]);
}

build(1, 1, n);

其中 \(Max_u\) 表示节点 \(u\) 的值，\(l,r\) 分别表示当前区间左右端点。

单点修改

可以发现，当修改某个点的值时，并不需要把所有的结果全部重新算一遍，只有对应节点的祖先需要修改，例如当将 \(A_3\) 修改为 \(2\) 时，线段树会变成这样：

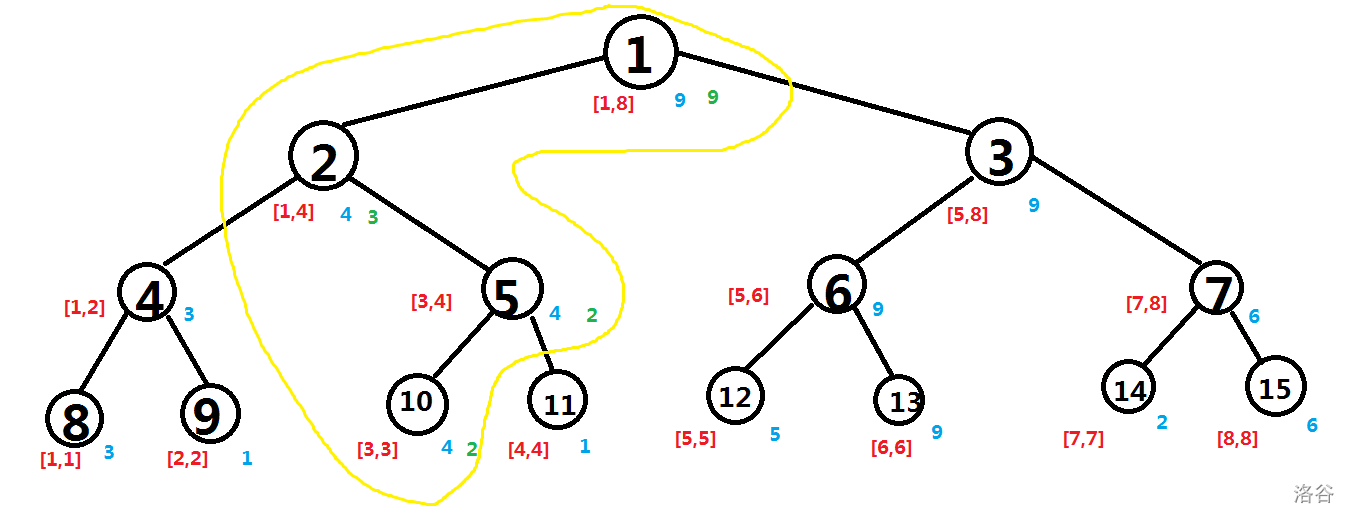
其中黄色的是改变了的部分，绿色的是改变后的值。

所以我们就可以做到 \(O(\log N)\) 修改。

代码

void update(int u, int l, int r, int p, int x) {
  if(l == r) {
    Max[u] = x;
    return;
  }
  int mid = (l + r) >> 1;
  if(p <= mid) {
    update(2 * u, l, mid, p, x);
  }else {
    update(2 * u + 1, mid + 1, r, p, x);
  }
  Max[u] = max(Max[2 * u], Max[2 * u + 1]);
}

update(1, 1, n, p, x);

其中 \(p\) 表示修改的位置，\(x\) 表示修改后的值。

区间查询

线段树的查询也很简单，就是把一个大区间拆分成很多小区间，当区间与查询区间没有交集时就不计入，如果当前区间被查询区间完全包含，则直接返回。

这个查询乍一看好像是 \(O(N)\) 的，但实际上是 \(O(\log N)\) 的，可以这么解释：

比如我们查询 \([2,7]\) 中的最大值时：

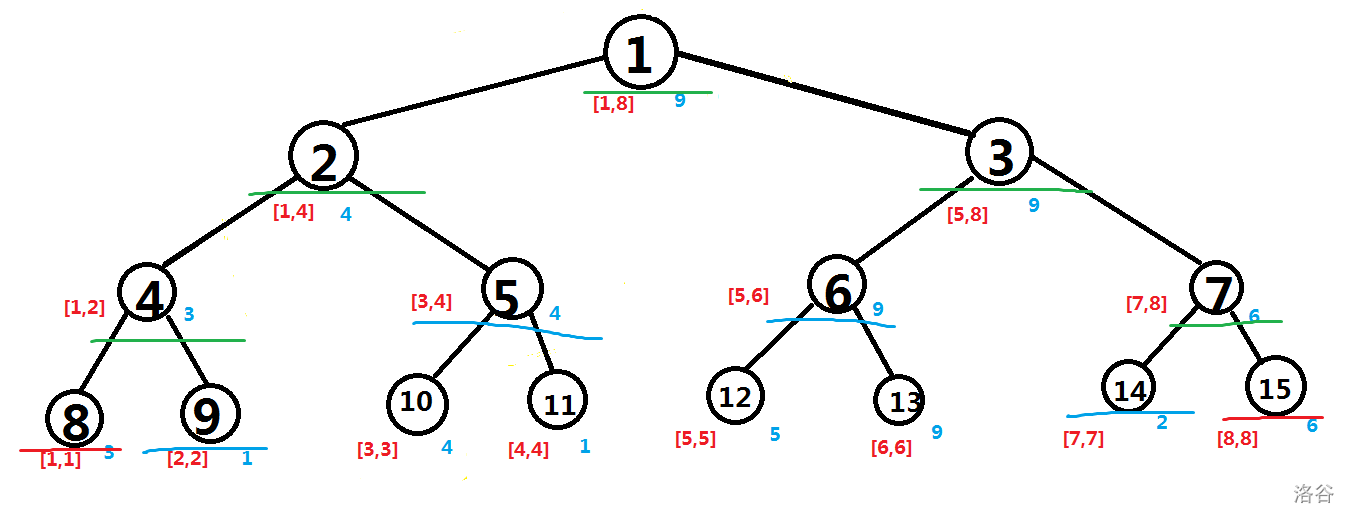
其中红色的点是与 \([2,7]\) 完全不重合的区间，蓝色的点是被 \([2,7]\) 完全包含的区间，绿色的是与 \([2,7]\) 部分相交的区间。

在每一层中，由于查询的是区间，所以蓝色的点一定是连续的一段。如果出现超过 \(2\) 个节点，那么必定有两个节点能合并为上一层中的区间，所以最多有两个蓝色节点，即总共最多有 \(2 \log N\) 个蓝色节点。红色同理。

可以发现，每多出一个绿色节点就会把两个子树合并。又因为红蓝色节点总数最多为 \(4 \log N\)，所以绿色节点最多有 \(4 \log N - 1\) 个。所以总时间复杂度为 \(2 \log N + 4 \log N - 1 = O(\log N)\)。

代码

int getmax(int u, int l, int r, int s, int t) {
  if(l >= s && r <= t) {
    return Max[u];
  }
  int mid = (l + r) >> 1, x = 0;
  if(l <= mid) {
    x = max(x, getmax(2 * u, l, mid, s, t));
  }
  if(r > mid) {
    x = max(x, getmax(2 * u + 1, mid + 1, r, s, t));
  }
  return x;
}

getmax(1, 1, n, s, t);

区间修改

如果还是使用原来的方法来进行区间修改时间就变成了 \(O(N)\)。可以考虑像区间查询查询那样：如果遇到一个被修改区间完全包含的区间，就直接返回，但要先更改那个节点的值。比如将 \([4,5]\) 修改为 \(6\)：

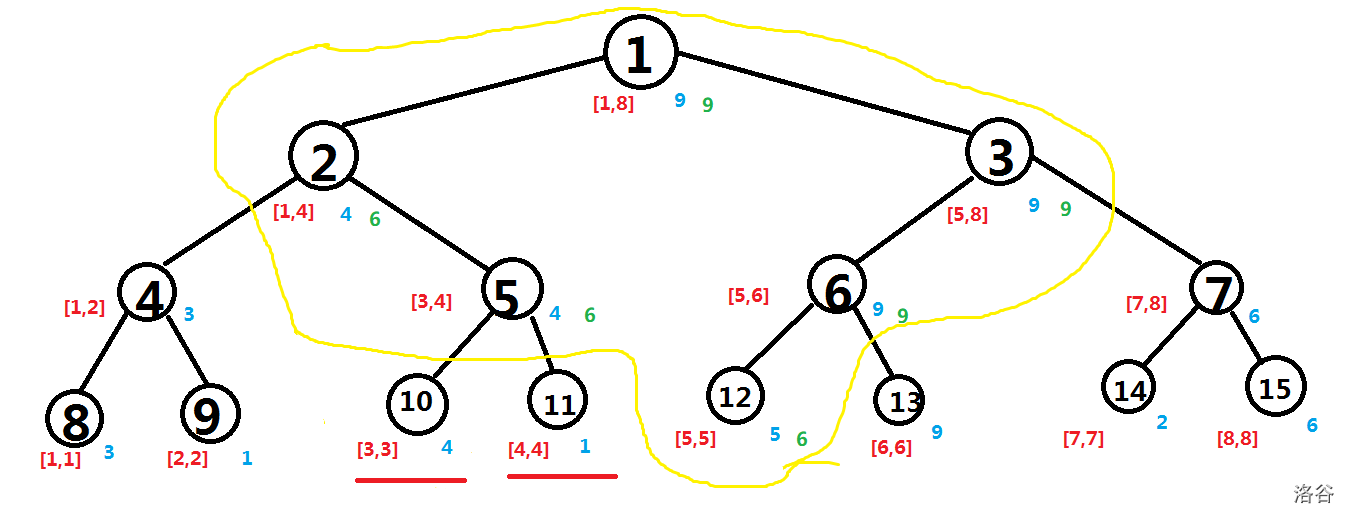
这样就可以用 \(O(\log N)\) 的时间复杂度进行修改了。可是画红线的两个节点就没有被更新到。很容易想到在这两个节点的父亲节点上打标记。如果发现需要访问（修改或查询）他的儿子时再更改他的儿子（记住还要将标记传给他的儿子，因为他的整颗子树都还没有更改）。而这就被称为懒惰标记。

代码

void update(int u, int l, int r, int s, int t, int x) {
  if(l >= s && r <= t) {
    Max[u] += x, c[u] += x;
    return;
  }
  if(c[u]) {
    Max[2 * u] += c[u], Max[2 * u + 1] += c[u];
    c[2 * u] += c[u], c[2 * u + 1] += c[u];
    c[u] = 0;
  }
  int mid = (l + r) >> 1;
  if(s <= mid) {
    update(2 * u, l, mid, s, t, x);
  }
  if(t > mid) {
    update(2 * u + 1, mid + 1, r, s, t, x);
  }
  Max[u] = max(Max[2 * u], Max[2 * u + 1]);
}

update(1, 1, n, l, r, x);

代码

单点修改

#include<bits/stdc++.h>
using namespace std;

const int MAXN = 200001;

int n, q, a[MAXN];

struct Segment_Tree {
  int l[4 * MAXN], r[4 * MAXN], Max[4 * MAXN];
  void build(int u, int s, int t) {
    l[u] = s, r[u] = t;
    if(s == t) {
      Max[u] = a[s];
      return;
    }
    int mid = (s + t) >> 1;
    build(2 * u, s, mid), build(2 * u + 1, mid + 1, t);
    Max[u] = max(Max[2 * u], Max[2 * u + 1]);
  }
  void update(int u, int p, int x) {
    if(l[u] == r[u]) {
      Max[u] = x;
      return;
    }
    if(p <= r[2 * u]) {
      update(2 * u, p, x);
    }else {
      update(2 * u + 1, p, x);
    }
    Max[u] = min(Max[2 * u], Max[2 * u + 1]);
  }
  int getmax(int u, int s, int t) {
    if(l[u] >= s && r[u] <= t) {
      return Max[u];
    }
    int x = 0;
    if(s <= r[2 * u]) {
      x = max(x, getmax(2 * u, s, t));
    }
    if(t >= l[2 * u + 1]) {
      x = max(x, getmax(2 * u + 1, s, t));
    }
    return x;
  }
}t;

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n;
  for(int i = 1; i <= n; ++i) {
    cin >> a[i];
  }
  t.build(1, 1, n);
  cin >> q;
  for(int i = 1, op, p, x, l, r; i <= q; ++i) {
    cin >> op;
    if(op == 1) {
      cin >> p >> x;
      t.update(1, p, x);
    }else {
      cin >> l >> r;
      cout << t.getmax(1, l, r) << "\n";
    }
  }
  return 0;
}

区间修改

#include<bits/stdc++.h>
using namespace std;

const int MAXN = 200001;

int n, q, a[MAXN];

struct Segment_Tree {
  int l[4 * MAXN], r[4 * MAXN], Max[4 * MAXN], c[4 * MAXN];
  void tag(int u, int x) {
    Max[u] += x, c[u] += x;
  }
  void pushdown(int u) {
    tag(2 * u, c[u]), tag(2 * u + 1, c[u]), c[u] = 0;
  }
  void build(int u, int s, int t) {
    l[u] = s, r[u] = t;
    if(s == t) {
      Max[u] = a[s];
      return;
    }
    int mid = (s + t) >> 1;
    build(2 * u, s, mid), build(2 * u + 1, mid + 1, t);
    Max[u] = max(Max[2 * u], Max[2 * u + 1]);
  }
  void update(int u, int s, int t, int x) {
    if(l[u] >= s && r[u] <= t) {
      tag(u, x);
      return;
    }
    pushdown(u);
    if(s <= r[2 * u]) {
      update(2 * u, s, t);
    }
    if(t >= l[2 * u + 1]) {
      update(2 * u + 1, s, t);
    }
    Max[u] = max(Max[2 * u], Max[2 * u + 1]);
  }
  int getmax(int u, int s, int t) {
    if(l[u] >= s && r[u] <= t) {
      return Max[u];
    }
    pushdown(u);
    int x = 0;
    if(s <= r[2 * u]) {
      x = max(x, getmax(2 * u, s, t));
    }
    if(t >= l[2 * u + 1]) {
      x = max(x, getmax(2 * u + 1, s, t));
    }
    return x;
  }
};

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n;
  for(int i = 1; i <= n; ++i) {
    cin >> a[i];
  }
  cin >> q;
  for(int i = 1, op, l, r, x; i <= q; ++i) {
    cin >> op >> l >> r;
    if(op == 1) {
      cin >> x;
      t.update(1, l, r, x);
    }else {
      cout << t.getmax(1, l, r) << "\n";
    }
  }
  return 0;
}