卷积神经网络的“卷积”操作不等于数学上定义的卷积操作
在介绍卷积神经网络CNN的时候，大部分教材在介绍“卷积操作”的时候都与下面这张图类似的说明
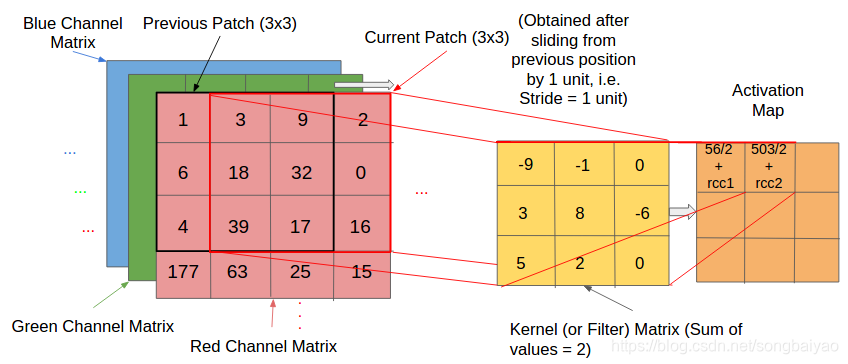
这点让人很困惑，因为在数学上，卷积运算是这么定义的
(
f
∗
g
)
(
t
)
=
∫
0
t
f
(
τ
)
g
(
t
−
τ
)
d
τ
(f * g )(t) = \int_{0}^{t} f(\tau) g(t - \tau)\, d\tau
(f∗g)(t)=∫0tf(τ)g(t−τ)dτ
很明显，在与
f
(
τ
)
f(\tau)
f(τ)相乘的是
g
(
t
−
τ
)
g(t-\tau)
g(t−τ)，而不是
g
(
t
+
τ
)
g(t+\tau)
g(t+τ)！而上图的卷积运算并不符合卷积的定义。事实上，卷积神经网络中的“卷积”操作其实是互相关运算(correlation operator)，而不是卷积运算(convolution operator)。他们的区别在于，卷积运算相当于把kernel进行上下左右翻转之后，再进行互相关运算。
