排序算法

归并排序

归并

 

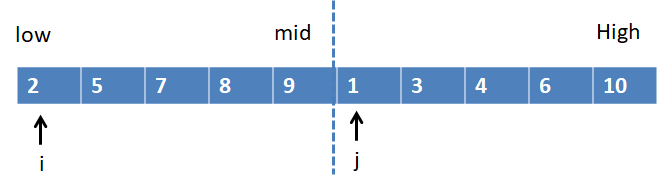
假设现在有一个列表分两段有序, 如何将其合成为一个有序列

 

 

思路:

 

 双指针i, j

1.分别从两段从左到右进行比较, 谁小则移动指针, 并把这个较小的数存入一个临时list中

2.遍历完成后可能存在有个有序段未到末端, 需要再使用一个while

3.将排好序的temp写后原list中

以上步骤称为一次归并

def merge(nums, low, mid, high):

    # 双指针 i,j 从左到右开始比较
    i = low
    j = mid + 1
    temp = []
    while i <= mid and j <= high:
        if nums[i] > nums[j]:
            temp.append(nums[j])
            j += 1
        else:
            temp.append(nums[i])
            i += 1

    # 遍历完成后可能存在有个有序段未到末端, 需要再使用一个while
    # 因为不清楚是哪段有序序列未到末端, 所以使用两个while循环
    while i <= mid:
        temp.append(nums[i])
        i += 1
    while j <= high:
        temp.append(nums[j])
        j += 1

    # 将排好序的temp写后原list中
    nums[low:high+1] = temp

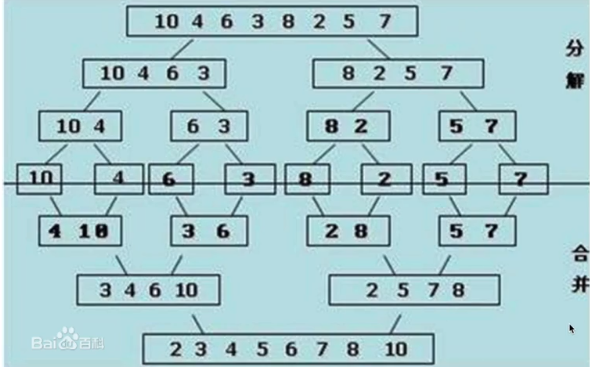
分解: 将列表越分越小, 直至分成一个元素(一个元素肯定是有序的)

终止条件: 一个元素是有序的

合并将两个有序列表归并, 列表越来越大

 

def merge_sort(nums, low, high):
    # 终止条件
    if low >= high:return
    # 将数组分为两部分
    mid = (low + high) // 2
    # 将左边排好序
    merge_sort(nums, low, mid)
    # 将有边排好序
    merge_sort(nums, mid + 1, high)
    # 将左右两边合并起来
    merge(nums, low, mid, high)

 两种高级排序算法的时间复杂度都是O(nlogn)

一般情况下, 就运行时间而言

　　快速排序 < 归并排序 < 堆排序

三种排序算法的缺点:

　　快速排序: 在极端情况下排序效率低

　　归并排序: 需要额外的内存开销

　　堆排序: 在块的排序算法中相对较慢