第七节:图结构详解(结构封装、添加定点/边、广度/深度优先遍历)
一. 图详解
1. 邻接矩阵
(1). 说明
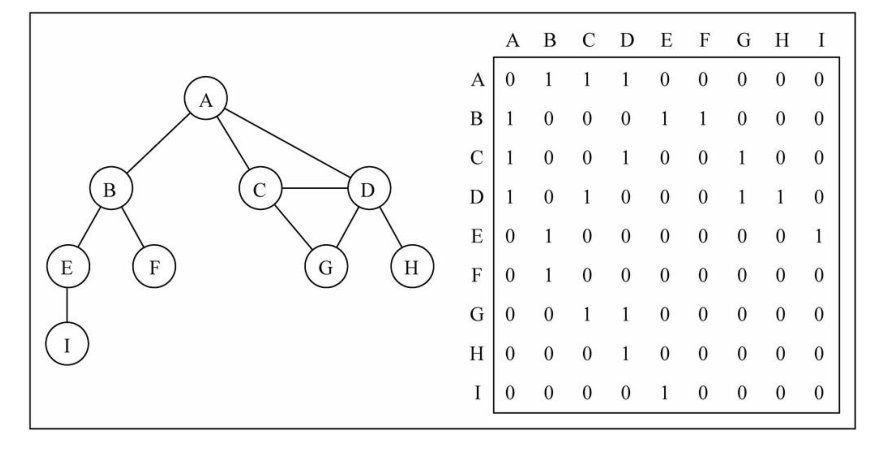
邻接矩阵让每个节点和一个整数项关联,该整数作为数组的下标值。
我们用一个二维数组来表示顶点之间的连接。
二维数组[0][2] -> A -> C
(2). 解析
在二维数组中,0表示没有连线,1表示有连线。
通过二维数组,我们可以很快的找到一个顶点和哪些顶点有连线。(比如A顶点,只需要遍历第一行即可)
另外,A - A,B - B(也就是顶点到自己的连线),通常使用0表示
(3). 弊端
邻接矩阵还有一个比较严重的问题,就是如果图是一个稀疏图
那么矩阵中将存在大量的0,这意味着我们浪费了计算机存储空间来表示根本不存在的边。
2. 邻接表(推荐)
(1). 说明
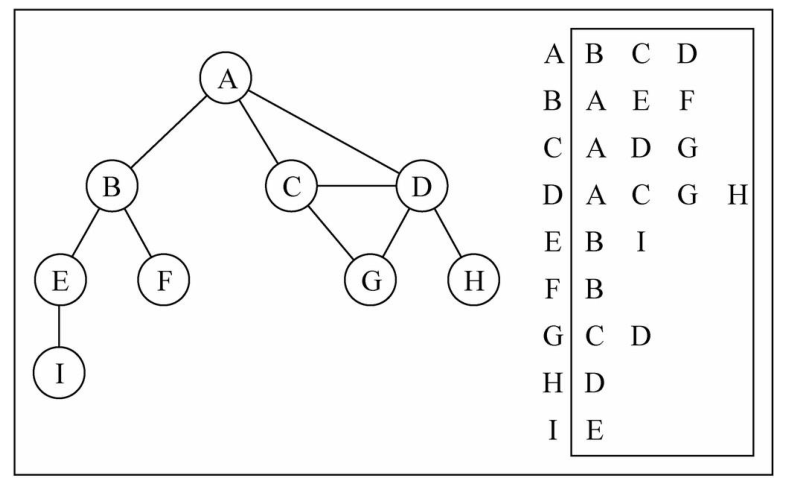
邻接表由图中每个顶点以及和顶点相邻的顶点列表组成。
这个列表有很多种方式来存储: 数组/链表/字典(哈希表)都可以。
(2). 解析
比如我们要表示和A顶点有关联的顶点(边),A和B/C/D有边,
那么我们可以通过A找到对应的数组/链表/字典,再取出其中的内容就可以啦。
(3). 弊端
邻接表计算"出度"是比较简单的(出度: 指向别人的数量,入度: 指向自己的数量)
邻接表如果需要计算有向图的"入度",那么是一件非常麻烦的事情。
它必须构造一个“逆邻接表”,才能有效的计算“入度”。但是开发中“入度”相对用的比较少。
二. 图的封装
1. Map结构复习
(1) 定义
Map是ES6中新增的一种数据结构,他类似Object,也是键值对集合,但是它的key不限于字符串,可以是任意类型,是一种更加完善的Hash结构。
(2) 常用的方法
size、set、get、has、delete、clear、forEach、for-of
{
let obj1 = { name: "ypf1" };
let obj2 = { name: "ypf2" };
//实例化1
let map = new Map();
map.set(obj1, "aaaa");
map.set(obj2, "bbb");
//实例化2
let map2 = new Map([
[obj1, "ccc"],
[obj2, "ddd"],
]);
// 遍历
map2.forEach((item, key) => {
console.log(`key:${key.name}},value:${item}`);
});
}2. 基本结构封装
(1). 思路:这里采用“邻接表”的模式进行存储,邻接表由图中每个顶点以及和顶点相邻的顶点列表组成
(2). 实操: 定义了两个属性:
✓ vertexes: 用于存储所有的顶点,我们说过使用一个数组来保存。
✓ adjList: adj是adjoin的缩写,邻接的意思。 adjList用于存储所有的边,我们这里采用邻接表的形式
class Graph<T> {
// 顶点
private verteces: T[] = [];
// 边:邻接表 (map中的key就是顶点,value是与该顶点相邻边的顶点,两个顶点就能组成一条边)
private adjList: Map<T, T[]> = new Map();
}
3. 添加方法封装
(1). 添加顶点
A.我们将添加的顶点放入到数组中。
B.另外,我们给该顶点创建一个数组[],该数组用于存储顶点连接的所有的边.
(2). 添加边
A.添加边需要传入两个顶点v1,v2,因为边是两个顶点之间的边,边不可能单独存在。
B.根据顶点v1取出对应的数组,将v2加入到它的数组中。
C.根据顶点v2取出对应的数组,将v1加入到它的数组中。
D.因为我们这里实现的是无向图,所以边是可以双向的。
/**
* 1.添加顶点
* @param vertex 添加的顶点
*/
addVertex(vertex: T) {
// 添加顶点
this.verteces.push(vertex);
// 添加顶点
this.adjList.set(vertex, []);
}
/**
* 2. 添加边 (两个顶点组成一条边)
* @param v1 顶点1
* @param v2 顶点2
*/
addEdge(v1: T, v2: T) {
// 分别以v1、v2顶点为主,添加对应关系
this.adjList.get(v1)?.push(v2);
this.adjList.get(v2)?.push(v1);
}
/**
* 3. 打印顶点对应的边
*/
printEdge() {
this.verteces.forEach(vertex => {
console.log(`${vertex} ----> ${this.adjList.get(vertex)?.join(",")}`);
});
}
4. 遍历-广度优先搜索(Breadth-First Search,简称BFS)
(1).含义
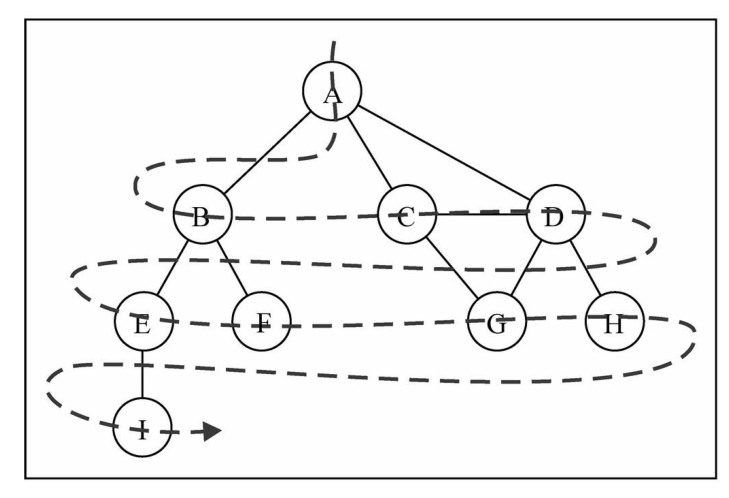
广度优先算法会从指定的第一个顶点开始遍历图,先访问其所有的相邻点,就像一次访问图的一层
(2).思路
采用队列解决,出队的同时将与相邻边的节点入队,直到队列中没有元素位置。(同二叉搜索树的层序遍历)
但是有一点不同:图的边是无序双向的,所以要记录访问过的顶点,不再访问了,否则就进入死循环了
(3).实操
A. 判断顶点是否为空
B. 用数组模拟队列, 并将第一个顶点入队
C. 创建Set结构,用来存放访问过的节点
D. 遍历队列,出队的同时将相邻节点入队,但前提是这个相邻的节点未被访问过
/**
* 4. 广度优先搜索
*/
bfs() {
//1. 判断顶点是否为空
if (this.verteces.length === 0) return;
//2. 创建队列,并将第一个顶点入队
let queue: T[] = [];
queue.push(this.verteces[0]);
//3.创建set结构,用来存放访问过的节点
let visitedSet = new Set();
visitedSet.add(this.verteces[0]);
//4. 遍历队列,出队的同时将相邻节点入队
while (queue.length > 0) {
//4.1 出队
let vt = queue.shift()!;
console.log(vt); //
//4.2 相邻节点入队, 但是要判断该节点是否访问过
let neighbors = this.adjList.get(vt);
//类型缩小, continue的作用表示跳出当前循环,进行下一次
if (!neighbors) continue;
//遍历(上面有了if判断,这里的neighbors肯定不为空,就不用写成neighbors?.xxx)
neighbors.forEach(item => {
if (!visitedSet.has(item)) {
visitedSet.add(item); // 加入set结构,表示已经访问过
queue.push(item); //入队
}
});
}
}
5. 遍历-深度优先搜索(Depth-First Search,简称DFS)
(1).含义
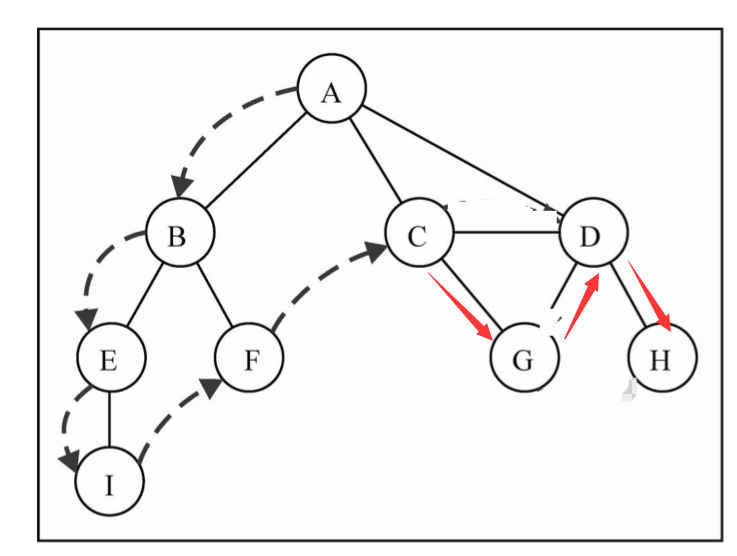
会从第一个指定的顶点开始遍历图,沿着路径直到这条路径最后被访问
(2).思路
利用栈来解决,出栈的同时,将相邻边的节点"逆序"入栈, 直到栈中没有元素 (不是很好理解,结合图来)
另外:也需要记录访问过的节点,防止重复入栈进入了死循环
(3).实操
A. 判断顶点是否为空
B. 用数组模拟栈, 并将第一个顶点入栈
C. 创建Set结构,用来存放访问过的节点
D. 遍历栈,出栈的同时将相邻节点“逆序入栈”,但前提是这个相邻的节点未被访问过
dfs() {
//1. 判断顶点是否为空
if (this.verteces.length === 0) return;
//2. 创建队列,并将第一个顶点入队
let stack: T[] = [];
stack.push(this.verteces[0]);
//3.创建set结构,用来存放访问过的节点
let visitedSet = new Set();
visitedSet.add(this.verteces[0]);
//4. 遍历队列,出队的同时将相邻节点入队
while (stack.length > 0) {
//4.1 出队
let vt = stack.pop()!;
console.log(vt); //
//4.2 相邻节点入队, 但是要判断该节点是否访问过
let neighbors = this.adjList.get(vt);
//类型缩小, continue的作用表示跳出当前循环,进行下一次
if (!neighbors) continue;
//遍历(上面有了if判断,这里的neighbors肯定不为空,就不用写成neighbors?.xxx)
for (let i = neighbors.length - 1; i >= 0; i--) {
let item = neighbors[i];
if (!visitedSet.has(item)) {
visitedSet.add(item); // 加入set结构,表示已经访问过
stack.push(item); //入队
}
}
}
}5. 测试
let graph = new Graph();
// 添加顶点
graph.addVertex("A");
graph.addVertex("B");
graph.addVertex("C");
graph.addVertex("D");
graph.addVertex("E");
graph.addVertex("F");
graph.addVertex("G");
graph.addVertex("H");
graph.addVertex("I");
// 添加边(邻接表)
graph.addEdge("A", "B");
graph.addEdge("A", "C");
graph.addEdge("A", "D");
graph.addEdge("C", "D");
graph.addEdge("C", "G");
graph.addEdge("D", "G");
graph.addEdge("D", "H");
graph.addEdge("B", "E");
graph.addEdge("B", "F");
graph.addEdge("E", "I");
//打印边
// graph.printEdge();
//广度优先遍历
// graph.bfs();
//深度优先遍历
graph.dfs();
!
- 作 者 : Yaopengfei(姚鹏飞)
- 博客地址 : http://www.cnblogs.com/yaopengfei/
- 声 明1 : 如有错误,欢迎讨论,请勿谩骂^_^。
- 声 明2 : 原创博客请在转载时保留原文链接或在文章开头加上本人博客地址,否则保留追究法律责任的权利。



