第四节：时间、空间复杂度的详解(大O表示法)
一. 时间复杂度
1. 现实案例
举个例子（现实的例子）：在一个庞大的图书馆中，我们需要找一本书。 在图书已经按照某种方式摆好的情况下（数据结构是固定的）
◼ 方式一：顺序查找
一本本找，直到找到想要的书；（累死）
◼ 方式二：先找分类，分类中找这本书
先找到分类，在分类中再顺序或者某种方式查找；
◼ 方式三：找到一台电脑，查找书的位置，直接找到；
图书馆通常有自己的图书管理系统；
利用图书管理系统先找到书的位置，再直接过去找到；
2. 程序案例
方式一 : 顺序查找
这种算法从头到尾遍历整个数组，依次比较每个元素和给定元素的值。
如果找到相等的元素，则返回下标；如果遍历完整个数组都没找到，则返回-1。
/**
* 顺序查找
* @param array 数据源，数组
* @param target 需要查找的目标对象
* @returns 目标对象的下标，如果不存在，返回-1
*/
function sequentSearch(array: number[], target: number): number {
let length = array.length;
for (let i = 0; i < length; i++) {
if (array[i] === target) return i;
}
return -1;
}
// 测试
let myArray = [2, 4, 56, 7, 8, 10, -3];
console.log(sequentSearch(myArray, 56)); //2
console.log(sequentSearch(myArray, -3)); //6
console.log(sequentSearch(myArray, 7)); //3
export default sequentSearch;
方式二 ：二分查找
这种算法假设数组是有序的，每次选择数组中间的元素与给定元素进行比较。
如果相等，则返回下标；如果给定元素比中间元素小，则在数组的左半部分继续查找；
如果给定元素比中间元素大，则在数组的右半部分继续查找；
这样每次查找都会将查找范围减半，直到找到相等的元素或者查找范围为空；
/*
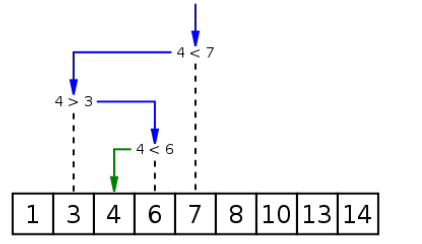
二分查找
原理：
1. 这种算法假设【数组是有序的！！！】，每次选择数组中间的元素与给定元素进行比较。
2. 如果相等，则返回下标；如果给定元素比中间元素小，则在数组的左半部分继续查找；
3. 如果给定元素比中间元素大，则在数组的右半部分继续查找；
4. 这样每次查找都会将查找范围减半，直到找到相等的元素或者查找范围为空；
用到的方法：
math.floor() 取下整 , 中间值： Math.floor((right + left) / 2)
重点理解：while (left <= right)
*/
/**
* 二分查找
* @param array 数据源，数组
* @param target 需要查找的目标对象
* @returns 目标对象的下标，如果不存在，返回-1
*/
function binarySearch(array: number[], target: number): number {
let left = 0; //左边索引
let right = array.length - 1; //右边索引
// 开始查找
while (left <= right) {
let mid = Math.floor((right + left) / 2);
if (array[mid] === target) {
return mid;
} else if (array[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
// 测试
let myArray = [2, 4, 5, 7, 8, 10, 12]; //必须是有顺序的
console.log(binarySearch(myArray, 5)); //2
console.log(binarySearch(myArray, 12)); //6
console.log(binarySearch(myArray, 7)); //3
console.log(binarySearch(myArray, 2)); //0
export default binarySearch;
3. 用时测试
代码分享
import sequentSearch from "./01-查找算法-顺序查找";
import binarySearch from "./02-查找算法-二分查找";
import { testOrderSearchEfficiency } from "hy-algokit";
// 声明数组
const MAX_LENGTH = 10000000;
const array = new Array(MAX_LENGTH).fill(0).map((_, index) => index);
const target = MAX_LENGTH / 2;
//顺序算法测试
const startTime = performance.now();
const index = sequentSearch(array, target); //顺序查找
const endTime = performance.now();
console.log(`索引的位置 ：${index},消耗的时间：${endTime - startTime}`);
//二分查找测试
const startTime2 = performance.now();
const index2 = binarySearch(array, target); //二分查找
const endTime2 = performance.now();
console.log(`索引的位置 ：${index2},消耗的时间：${endTime2 - startTime2}`);
// 调用封装的测试
testOrderSearchEfficiency(sequentSearch);
testOrderSearchEfficiency(binarySearch);
export {};测试结果
结论：
顺序查找算法的时间复杂度是O(n)
二分查找算法的时间复杂度是O(log n)
二. 大O表示法
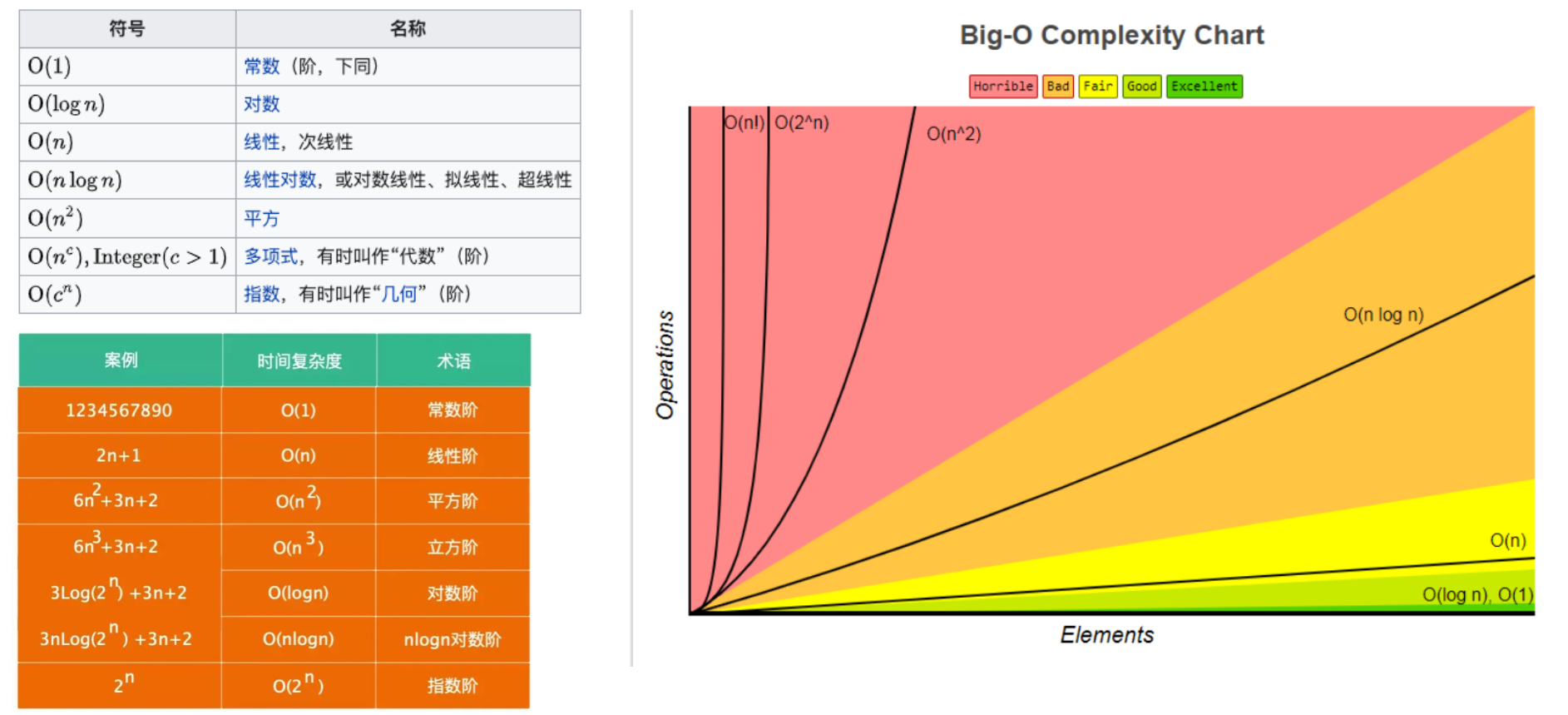
1. 概念
大O表示法（Big O notation）英文翻译为大O符号（维基百科翻译），中文通常翻译为大O表示法（标记法）
2. 举例推导过程
3. 常用的函数阶
三. 空间复杂度
1. 概念
空间复杂度指的是程序运行过程中所需要的额外存储空间。
空间复杂度也可以用大O表示法来表示；
空间复杂度的计算方法与时间复杂度类似，通常需要分析程序中需要额外分配的内存空间，如数组、变量、对象、递归调用等。
2. 举例说明
(1) 对于一个简单的递归算法来说，每次调用都会在内存中分配新的栈帧，这些栈帧占用了额外的空间。
因此，该算法的空间复杂度是O(n)，其中n是递归深度。
(2) 而对于迭代算法来说，在每次迭代中不需要分配额外的空间，因此其空间复杂度为O(1)。
PS：当空间复杂度很大时，可能会导致内存不足，程序崩溃。
3. 数据和链表复杂度对比
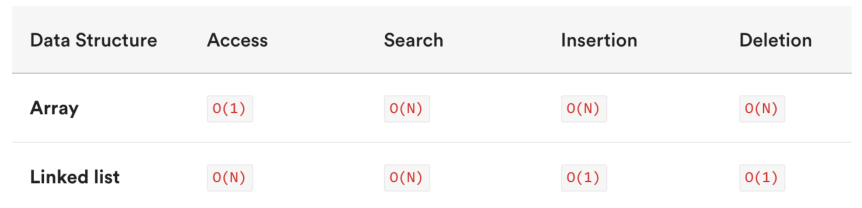
(1). 数组是一种连续的存储结构，通过下标可以直接访问数组中的任意元素。
时间复杂度：对于数组，随机访问时间复杂度为O(1)，插入和删除操作时间复杂度为O(n)。
空间复杂度：数组需要连续的存储空间，空间复杂度为O(n)。
(2). 链表是一种链式存储结构，通过指针链接起来的节点组成，访问链表中元素需要从头结点开始遍历。
时间复杂度：对于链表，随机访问时间复杂度为O(n)，插入和删除操作时间复杂度为O(1)。
空间复杂度：链表需要为每个节点分配存储空间，空间复杂度为O(n)。
结论
如果数据量不大，且需要频繁随机访问元素，使用数组可能会更好。
如果数据量大，或者需要频繁插入和删除元素，使用链表可能会更好
!
- 作 者 : Yaopengfei(姚鹏飞)
- 博客地址 : http://www.cnblogs.com/yaopengfei/
- 声 明1 : 如有错误，欢迎讨论，请勿谩骂^_^。
- 声 明2 : 原创博客请在转载时保留原文链接或在文章开头加上本人博客地址，否则保留追究法律责任的权利。
