第九节：树与二叉树深度剖析(一)
一. 树简介
1. 定义
(1) 树结构是一种非线性存储结构，存储的是具有“一对多”关系的数据元素的集合。
(2) 树（Tree）是n(n≥0)个节点（Node）的有限集合。在任意一颗非空树中，有且仅有一个特定的成为根(Root)的节点，当n＞1时，其余节点分成m（m＞0）个互不相交的有限集T1，T2，……，Tm，其中每一个集合本身又是一棵树，并且称为根的子树。树的定义是递归的，即在树的定义中又用到了树的概念，它刻画了树固有的特性，即一棵树有若干个子树构成，而子树又由更小的若干子树构成。
(3) 树的逻辑特征可以描述为：树中任一节点都可以有0个或多个后继节点（孩子），但至多只能由一个前驱节点（双亲），树中只有根节点没有前驱，叶子节点无后继。
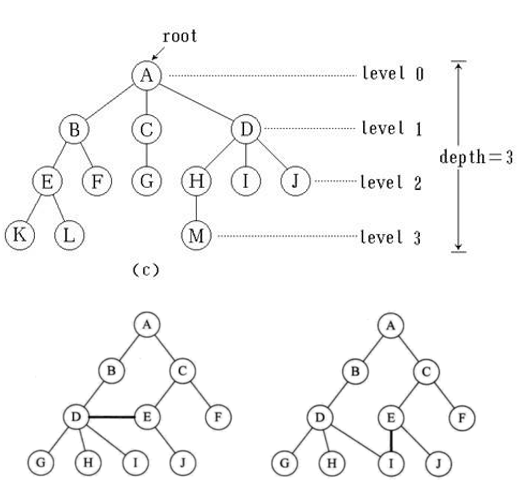
2. 一些概念
树的节点：使用树结构存储的每一个数据元素都被称为“结点”
节点的度：对于一个结点，拥有的子树数（结点有多少分支）称为结点的度
树的度：树内各节点度的最大值。
叶子或终端节点：度为0的节点。
非终端节点或分支节点：度不为0的节点。
孩子和双亲：节点的子树的个根成为该节点的孩子。该节点成为孩子的双亲或父亲。
兄弟：同一个双亲的孩子成为兄弟。
祖先和子孙：节点的祖先是从根到该节点所经分支上的所有节点。反之，以某节点为根的子树中的任一节点都成为该节点的子孙。
层数和堂兄弟：层数从根节点开始定义，根为第一层，根的孩子为第二层，其余节点的层数为双亲节点层数+1.双亲在同一层的节点互为堂兄弟。
树的深度：树节点中的最大层数称为树的深度。
有序树和无序树：树中节点的各子树从左至右是有次序的成为有序树，否则为无序树。
森林：有限棵树的集合。对树而言，删去根节点，得到森林。对森林而言，加上根节点变为一棵树
二. 二叉树简介
1. 定义
本身是有序树，树中包含的各个节点的度不能超过 2，即只能是 0、1 或者 2。
二叉树有五中基本形态：空二叉树，仅有根节点的二叉树，右子树为空的二叉树，左子树为空的二叉树，左右子树均非空的二叉树。如下图：
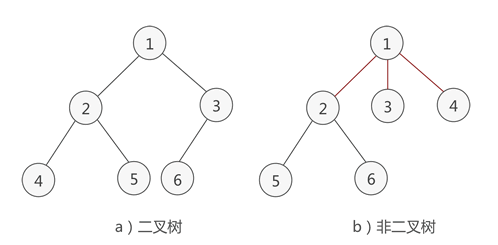
2. 二叉树的性质
(1). 二叉树中，第 i 层最多有 2i-1 个结点。
(2). 如果二叉树的深度为 K，那么此二叉树最多有 2K-1 个结点。
(3). 二叉树中，终端结点数（叶子结点数）为 n0，度为 2 的结点数为 n2，则 n0=n2+1。
PS:
性质 3 的计算方法为：对于一个二叉树来说，除了度为 0 的叶子结点和度为 2 的结点，剩下的就是度为 1 的结点（设为 n1），那么总结点 n=n0+n1+n2。
同时，对于每一个结点来说都是由其父结点分支表示的，假设树中分枝数为 B，那么总结点数 n=B+1。而分枝数是可以通过 n1 和 n2 表示的，即 B=n1+2*n2。所以，n 用另外一种方式表示为 n=n1+2*n2+1。两种方式得到的 n 值组成一个方程组，就可以得出 n0=n2+1。
3. 满二叉树
(1). 定义：如果二叉树中除了叶子结点，每个结点的度都为 2，则此二叉树称为满二叉树。
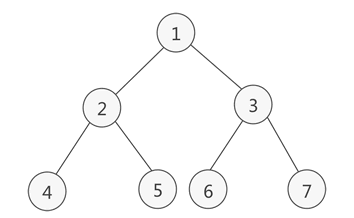
(2). 性质：除了普通二叉树的性质外，还有以下特性
A. 满二叉树中第 i 层的节点数为 2n-1 个。
B. 深度为 k 的满二叉树必有 2k-1 个节点 ，叶子数为 2k-1。
C. 满二叉树中不存在度为 1 的节点，每一个分支点中都两棵深度相同的子树，且叶子节点都在最底层。
D. 具有 n 个节点的满二叉树的深度为 log2(n+1)。
4. 完全二叉树
(1).定义：如果二叉树(首先得是个二叉树)中除去最后一层节点为满二叉树，且最后一层的结点依次从左到右分布，则此二叉树被称为完全二叉树。
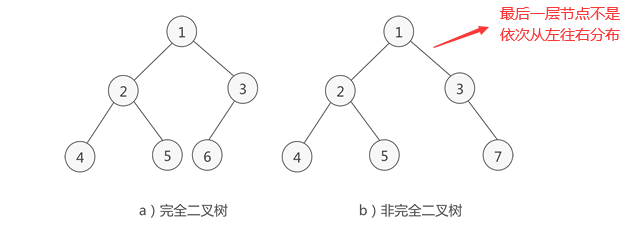
(2).性质：除了普通二叉树的性质外，还有以下特性
对于任意一个完全二叉树来说，如果将含有的结点按照层次从左到右依次标号（如图 3a），对于任意一个结点 i ，完全二叉树还有以下几个结论成立：
A. 当 i>1 时，父亲结点为结点 [i/2] 。（i=1 时，表示的是根结点，无父亲结点）
B. 如果 2*i>n（总结点的个数） ，则结点 i 肯定没有左孩子（为叶子结点）；否则其左孩子是结点 2*i 。
C. 如果 2*i+1>n ，则结点 i 肯定没有右孩子；否则右孩子是结点 2*i+1 。
三. 二叉树存储结构
1.顺序存储结构
(1).含义
二叉树的顺序存储指用数组进行存储二叉树，但需要注意顺序存储仅仅适用于完全二叉树.
(2).原理
把一棵二叉树自上而下，从左到右顺序编号，并把编号一次存放在数组内，可以得到如图所示的结果，设满二叉树结点在数组中的索引号为i，那么有如下性质：
1.如果i=0，则结点为根节点，无双亲
2.如果i>0,则双亲节点为（i-1）/2
3.节点为i的左孩子为2i+1，右孩子为2i+2
4.如果i>0,i为奇数时，他是双亲结点的左孩子，他的兄弟为i+1，i为偶数时，他是双亲的右孩子，兄弟为i-1
5.深度为k的满二叉树需要长度为2k-1的数组进行存储。
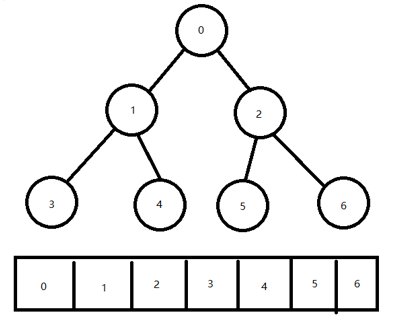
(3). 优点：
使用数组存放满二叉树是非常方便的，可以根据结点的索引号快速推算出他的双亲，孩子和兄弟，所以他是存储满二叉树最简单，最节省空间的做法。
(4). 缺点：
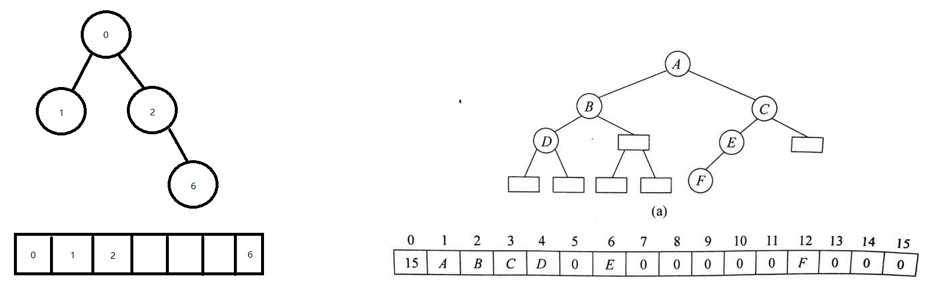
结点在数组中的位置反映出结点之间的关系，存储一般二叉树的时候，只需要将数组中的空结点所对应的位置为空即可，如图，这会造成一定的空间浪费，但如果空结点不多，这些浪费可以忽略。
一个深度为k的二叉树需要2k-1个存储空间，当k值很大并且二叉树的空结点很多时，最坏的情况是每层只有一个结点，使用顺序存储显然会造成极大的浪费，这时我们就应该使用链式存储结构来存储二叉树的数据。
2.链式存储结构
(1).含义
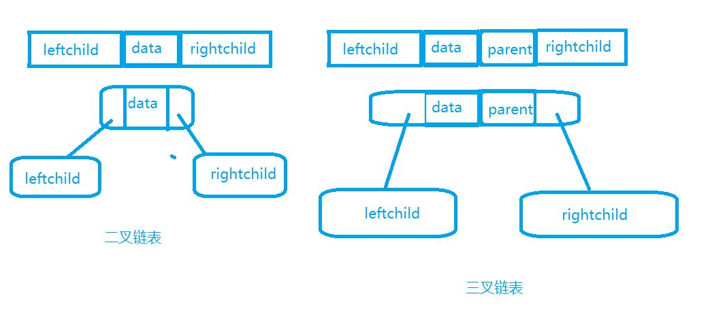
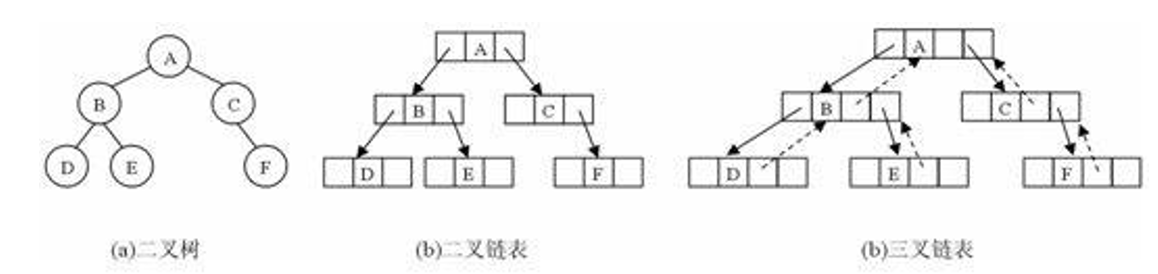
二叉树的链式存储结构可分为二叉链表和三叉链表。二叉链表中，每个结点出了存储本身的数据外，还应该设置两个指针域left和right，分别指向其左孩子和右孩子。如图，这样访问孩子的时间复杂度为O（1），但是访问双亲的复杂度为O（n）
三叉链表是在二叉链表上的改进，除了存储左右孩子的指针外，另外在加一个指向双亲的指针域parent，如图：
四. 二叉树的遍历
1. 说明
二叉树的遍历就是按照某种顺序对树中的每个节点访问且只能访问一次的过程。树遍历的本质是将非线性化结构线性化，他是二叉树各种运算和操作的实现基础。二叉树遍历分为深度优先遍历和广度优先遍历。
2. 深度优先遍历
深度优先遍历是使用递归的方法来访问每一个结点的。每棵二叉树都是有数据，左子树，右子树这三个基础部分组成，如果递归遍历这三个部分，也就遍历了整棵二叉树。
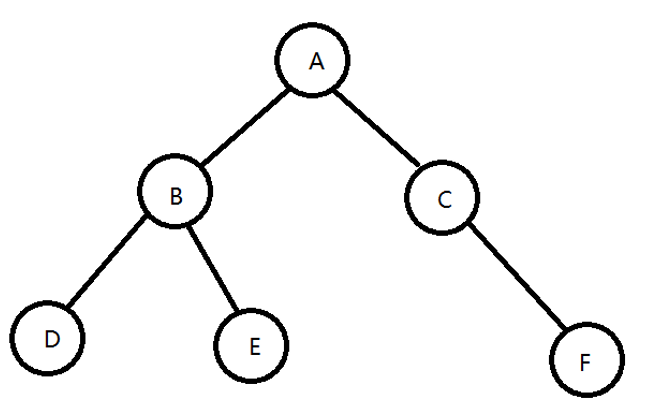
(1).先序遍历：访问根节点→访问当前节点的左子树→若当前节点的无左子树，则访问当前节点右子树。 下图遍历结果为：ABDECF
(2).中序遍历：访问当前节点的左子树→访问根节点→访问当前节点右子树。 下图遍历结果为：DBEACF
(3).后序遍历：从根节点出发，依次遍历各节点的左右子树，直到当前节点左右子树遍历完成后，才访问该节点元素。下图遍历结果：DEBFCA
图示：
3.广度优先遍历
由于二叉树的结点分属不同的层次，因此可以从上而下，从左到右依次按层访问每个节点。他的访问顺序正好和之前所述二叉树顺序存储结构中结点在数组中的存放顺序相吻合。上图的遍历结果为：ABCDEF
代码分享：
二叉树节点类：
/// <summary> /// 二叉树节点类 /// </summary> public class Node { public Node Left { get; set; } //左孩子 public Node Right { get; set; } //右孩子 public object Data { get; set; } //数据 public Node(object data) { this.Data = data; } public override string ToString() { return Data.ToString(); } }
二叉树构建类和4种遍历算法：
/// <summary> /// 二叉树类 /// </summary> public class BinaryTree { /// <summary> /// 头结点 /// </summary> public Node Head { get; set; } /// <summary> /// 构建二叉树的字符串 /// </summary> private string cStr { get; set; } /// <summary> /// 构造方法 /// </summary> /// <param name="Str"></param> public BinaryTree(string Str) { this.cStr = Str; //保存构造字符串 this.Head = new Node(Str[0]); //添加头结点 //给头结点添加孩子节点 Add(this.Head, 0); } /// <summary> /// 添加节点 /// </summary> /// <param name="parent">父节点</param> /// <param name="index">父亲索引</param> private void Add(Node parent, int index) { int leftIndex = index * 2 + 1; //左孩子索引 int rightIndex = index * 2 + 2; //右孩子索引 if (leftIndex < cStr.Length) //左索引没有超过字符串长度 { if (cStr[leftIndex] != '#') //# 用来表示空节点 { parent.Left = new Node(cStr[leftIndex]); //继续递归调用添加左孩子节点 Add(parent.Left, leftIndex); } } if (rightIndex < cStr.Length) //右索引没有超过字符串长度 { if (cStr[rightIndex]!='#') //# 用来表示空节点 { parent.Right = new Node(cStr[rightIndex]); //继续递归调用添加右孩子节点 Add(parent.Right, rightIndex); } } } /// <summary> /// 先序遍历 /// </summary> /// <param name="node"></param> public void PreOrder(Node node) { if (node!=null) { Console.Write(node.ToString()); PreOrder(node.Left); //递归左 PreOrder(node.Right); //递归右 } } /// <summary> /// 中序遍历 /// </summary> /// <param name="node"></param> public void MidOrder(Node node) { if (node != null) { MidOrder(node.Left); //递归左 Console.Write(node.ToString()); MidOrder(node.Right); //递归右 } } /// <summary> /// 后序遍历 /// </summary> /// <param name="node"></param> public void AfterOrder(Node node) { if (node != null) { AfterOrder(node.Left); //递归左 AfterOrder(node.Right); //递归右 Console.Write(node.ToString()); } } /// <summary> /// 广度优先遍历 /// </summary> public void LevelOrder() { Queue<Node> queue = new Queue<Node>(); //创建队列 queue.Enqueue(this.Head); //根节点入队 while (queue.Count>0) // { Node node = queue.Dequeue(); //出队 Console.Write(node.ToString()); if (node.Left!=null) { //将左孩子入队 queue.Enqueue(node.Left); } if (node.Right!=null) { //将右孩子入队 queue.Enqueue(node.Right); } } } }
调用：
{ Console.WriteLine("-------------------二叉树遍历测试-------------------"); string Str= "ABCDE#F"; BinaryTree bTree = new BinaryTree(Str); Console.WriteLine("先序遍历:"); bTree.PreOrder(bTree.Head); Console.WriteLine(); Console.WriteLine("中序遍历:"); bTree.MidOrder(bTree.Head); Console.WriteLine(); Console.WriteLine("后序遍历:"); bTree.AfterOrder(bTree.Head); Console.WriteLine(); Console.WriteLine("广度优先遍历:"); bTree.LevelOrder(); }
运行结果：
!
- 作 者 : Yaopengfei(姚鹏飞)
- 博客地址 : http://www.cnblogs.com/yaopengfei/
- 声 明1 : 如有错误，欢迎讨论，请勿谩骂^_^。
- 声 明2 : 原创博客请在转载时保留原文链接或在文章开头加上本人博客地址，否则保留追究法律责任的权利。
