06回归算法

一.线性回归

1.定义

线性回归通过一个或者多个自变量与因变量之间之间进行建模的回归分析。其中特点为一个或多个称为回归系数的模型参数的线性组合。

2.公式

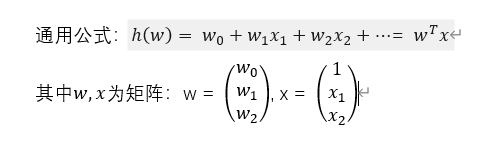
3.损失函数

检验误差大小：

• 为第个训练样本的真实值
• 为第个训练样本特征值组合预测函数

总损失定义：

 

            

又称最小二乘法

目的是找到最小损失对应的W值

4.正规方程

求解：

X为特征值矩阵，y为目标值矩阵

缺点：当特征过于复杂，求解速度太慢

      对于复杂的算法，不能使用正规方程求解(逻辑回归等)

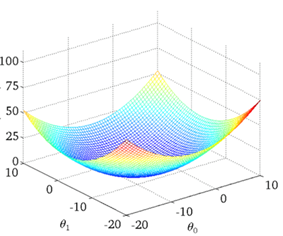
5.梯度下降

理解：沿着这个函数下降的方向找，然后不断改变W值，最后就能找到山谷的最低点，

使用：面对训练数据规模十分庞大的任务

 

 

 

6.API

l  sklearn.linear_model.LinearRegression  正规方程

l  sklearn.linear_model.SGDRegressor 梯度下降

coef_：回归系数

二.回归性能评估

1.均方误差

 

 

 

2.评估API：sklearn.metrics.mean_squared_error

• mean_squared_error(y_true, y_pred)
  • 均方误差回归损失
  • y_true:真实值
  • y_pred:预测值
  • return:浮点数结果

注：真实值，预测值为标准化之前的值

3.线性回归总结

特点：线性回归器是最为简单、易用的回归模型。

从某种程度上限制了使用，尽管如此，在不知道特征之间关系的前提下，我们仍然使用线性回归器作为大多数系统的首要选择。

小规模数据：LinearRegression(不能解决拟合问题)以及其它

大规模数据：SGDRegressor

三.过拟合与欠拟合

1.过拟合

一个假设在训练数据上能够获得比其他假设更好的拟合， 但是在训练数据外的数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。(模型过于复杂)

2.欠拟合

一个假设在训练数据上不能获得更好的拟合， 但是在训练数据外的数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。(模型过于简单)

3.欠拟合的原因及解决方法

1）原因：学习到数据的特征过少

2）解决办法：增加数据的特征数量

4. 过拟合原因以及解决办法

1）原因：原始特征过多，存在一些嘈杂特征。 模型过于复杂是因为模型尝试去兼顾各个测试数据点。

2）解决办法：

• 进行特征选择，消除关联性大的特征(很难做)
• 交叉验证(让所有数据都有过训练)
• 正则化(了解)

5.L2正则化

作用：可以使得W的每个元素都很小，都接近于0

优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象

四.岭回归

1.API：sklearn.linear_model.Ridge

sklearn.linear_model.Ridge(alpha=1.0)

• 具有l2正则化的线性最小二乘法
• alpha:正则化力度
• coef_:回归系数

2. 线性回归 LinearRegression与Ridge对比

岭回归：回归得到的回归系数更符合实际，更可靠。另外，能让估计参数的波动范围变小，变的更稳定。在存在病态数据偏多的研究中有较大的实用价值。

3.实例（正规方程，梯度下降，岭回归）

def mylinear():
    """
    线性回归直接预测房子价格
    :return: None
    """
    # 获取数据
    lb = load_boston()

    # 分割数据集到训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)

    print(y_train, y_test)

    # 进行标准化处理(?) 目标值处理？
    # 特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
    std_x = StandardScaler()

    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)

    # 目标值
    std_y = StandardScaler()

    y_train = std_y.fit_transform(y_train)
    y_test = std_y.transform(y_test)

    # 预测房价结果
    model = joblib.load("./tmp/test.pkl")

    y_predict = std_y.inverse_transform(model.predict(x_test))

    print("保存的模型预测的结果：", y_predict)

    # estimator预测
    # 正规方程求解方式预测结果
    lr = LinearRegression()

    lr.fit(x_train, y_train)

    print(lr.coef_)

    保存训练好的模型
    joblib.dump(lr, "./tmp/test.pkl")

    # 预测测试集的房子价格
    y_lr_predict = std_y.inverse_transform(lr.predict(x_test))

    print("正规方程测试集里面每个房子的预测价格：", y_lr_predict)

    print("正规方程的均方误差：", mean_squared_error(std_y.inverse_transform(y_test), y_lr_predict))

    # 梯度下降去进行房价预测
    sgd = SGDRegressor()

    sgd.fit(x_train, y_train)

    print(sgd.coef_)

    # 预测测试集的房子价格
    y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))

    print("梯度下降测试集里面每个房子的预测价格：", y_sgd_predict)

    print("梯度下降的均方误差：", mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))

    # 岭回归去进行房价预测
    rd = Ridge(alpha=1.0)

    rd.fit(x_train, y_train)

    print(rd.coef_)

    # 预测测试集的房子价格
    y_rd_predict = std_y.inverse_transform(rd.predict(x_test))

    print("梯度下降测试集里面每个房子的预测价格：", y_rd_predict)

    print("梯度下降的均方误差：", mean_squared_error(std_y.inverse_transform(y_test), y_rd_predict))

    return None