个人项目-数独
项目源代码的Github链接
https://github.com/yaoling1997/softwareFirstHomework
需求分析
一、生成数独
命令:sudoku.exe -c n
要求:
(1)输出到sudoku.txt
(2)不重复
(3)1<=n<=1000000
(4)可以处理异常情况,如:sudoku.exe -c abc
(5)左上角第一个数为(学号后两位相加)% 9 + 1=(9+9)%9+1=1
(6)参数不合法输出"invalid parameters"到文件
二、求解数独
命令:sudoku.exe -s absolute_path_of_puzzlefile
要求:
(1)输出到sudoku.txt
(2)0代表空格
(3)文件中数独题目数为n,1<=n<=1000000
(4)保证格式正确
(5)对每个数独题目求出一个可行解
(6)参数不合法输出"invalid parameters"到文件
解题思路
一、生成数独
第一步想到的是通过枚举每个格子的数字来生成数独,但是显然效率太低。通过上网查阅数独的相关知识,其中有一篇博客http://mouselearnjava.iteye.com/blog/1941483讲到了通过转换法来生成数独。
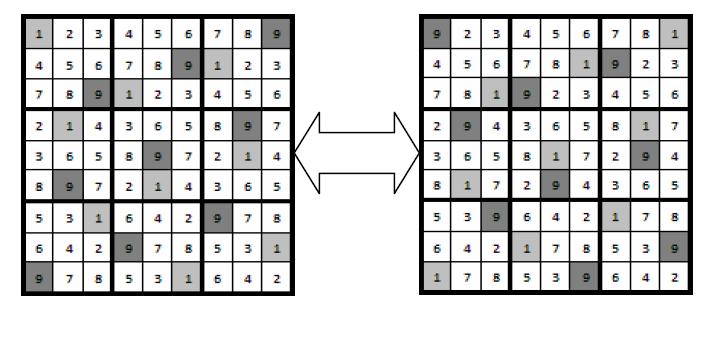
第一种方法是交换数字法,比如说将棋盘上所有1和9互换位置后仍然是一个可行的数独。
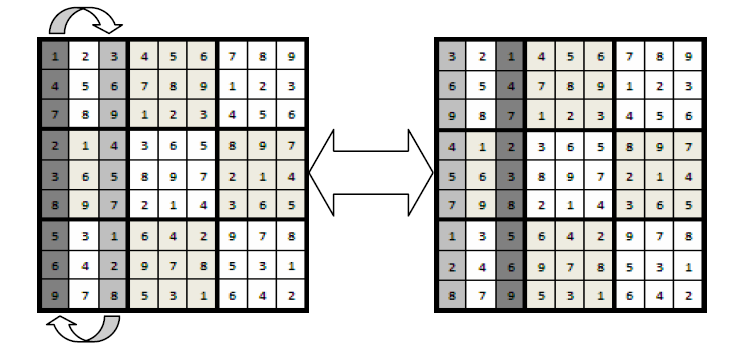
第二种方法是交换行列法,行和列的转换,需要保证的是:交换只发生在前三行,中间三行,最后三行,前三列,中间三列以及最后三列之间。而不能越界交换,比如第一行和第四行交换就是不允许的。 还有其余的一些方法,不过这里用不到。
经过和室友们的讨论,我们发现了一种基于变换来生成矩阵的方法。假设我们有一个正确的数独,我们可以通过数字交换法,将1~9分别映射到不同的排列来生成另外9!-1个数独。不过我们的题目要求左上角那个数字是固定的,于是通过第一种方法实际上共有8!=40320种数独,暂且称它们为种子。可题目要求最多可是要生成一百万个数独啊,怎么办呢?别急,接下来我们可以对这8!个种子应用行变换法。为了保证左上角的那个数字固定,我们做行变换时不考虑第一行。每3行分为一个组,第一组有不交换2、3行和交换2、3行两种方法,第二组和第三组都可以采取映射的方式,分别有3!=6种方法,所以对于第一种方法生成的每一个种子,我们可以再生成2*6*6-1=71个数独。所以我们一共生成了8!*2*3!*3!=2903040 种数独满足题目的数量要求。你可能会问,之后生成的数独会重复吗?我可以大声告诉你,不可能。不同的种子之间第一行是不一样的,所以它们通过行交换法生成的新数独也不会重复。
二、求解数独
一开始想到的是暴力枚举没有填数的地方,不过还是上网查阅一下资料比较好。这里有一篇博客http://www.cnblogs.com/grenet/archive/2013/06/19/3138654.html讲的比较详细。不过这篇博客用到的求解方法仍然是比较低端的暴力,只是有一些小优化。我在求解的时候先将所有的没填数字的格子存到一个栈中,找出每个格子可以填的数字,存放到对应的set中。在搜索的时候先从可填数字少的空格开始搜索,这样的话一旦这个格子填上数字后会使得剩下的某些格子可填的数字变少,从而可以更快地求出解。测试了一下10000组随机数据要跑74s左右。当然还有一些更高端的做法,比如说将数独转化为精确覆盖问题并用DLX算法求解。我是参考的刘汝佳大佬写的白书(算法竞赛入门经典——训练指南)写的,不过经测试对于自己构造的10000组随机数据DLX算法要跑109s,比一开始写的暴力都慢,不过DLX的最坏求解时间是要优于暴力的。小伙伴们可以尝试交一发poj3074,这题我写的DLX可以过但暴力过不了。不过最终我还是决定交暴力,所以DLX算法在这里就不过多叙述了。
本来是决定交暴力的,但是发现DLX慢是因为自己写的太丑了,用性能分析工具一看发现自己用的vector特别耗时间,改成数组后效率有了质的飞跃。所以这里还是简单介绍一下DLX算法的实现。我是主要是参考了白书的算法。首先我们要知道什么是精确覆盖问题(详情可以参考http://www.cnblogs.com/grenet/p/3145800.html)
有这么一个矩阵我们要选择一些行使得每一列有且仅有一个1
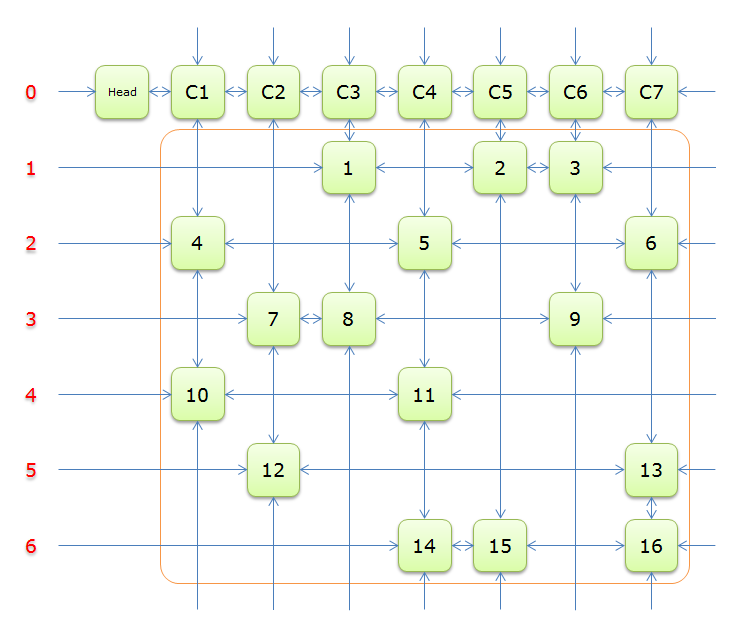
我们可以实现这么一个链表
第一行是新建的虚拟节点。每次递归时选择节点数最少的一列,然后枚举这一列上的行进行覆盖,记录选择的节点。覆盖的时候有会引起一些列的删除(所选行在对应列上有节点),这些新删的列有会引起一些行的删除(删除列在对应行上有节点)。递归会来有要还原链表的状态。当链表只剩下一个虚拟节点0时表示我们已经找到解了。
有了DLX算法,我们只需要将数独问题转化为精确覆盖问题就可以求解了。精确在覆盖问题的矩阵中,行代表决策,列代表需要满足的条件。我们可以将数独问题转化一下。(r,c,v)代表一个决策,在r行c列放数字v。需要满足的条件可以表示为:slot(a,b),a行b列缺数字;row(a,b),a行缺数字b;col(a,b),a列缺数字b;sub(a,b),第a个小矩形缺数字b。每个决策满足4个条件。因此链表一共9*9*9+1=729+1行(包括虚拟节点所占行),一共9*9*4=324列(不包括头节点),总共不超过9*9*9*4+324+1=3241个节点。构建好链表后就可以套用DLX算法求解啦!
设计实现
c++中我直接用结构体来实现数据的组织,根据需求和实现方法的不同分为了三个结构体:SolveC、SolveS、DLX、SolveS_DLX
SolveC:解决生成数独问题
其中包含三个函数,分别是:
(1)void initPermutation(int a[matrixLen])
用来生成用于映射的初始排列
(2)void rowChange(int row)
对当前种子进行行变换来获得新的数独,调用rowChange函数递归求解
(3)void solve()
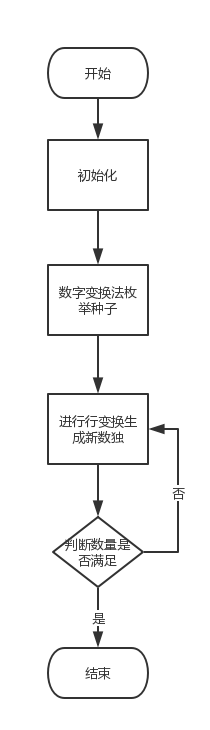
解决问题的入口,调用initPermutation函数生成用于映射的初始排列,负责实现数字交换法,并调用rowChange函数来生成新的数独
SolveS:解决求解数独问题
其中包含五个函数,分别是:
(1)void init()
在求解每一个数独问题前清空相应的数据结构
(2)void initSetOfThisEmptyPos(int x, int y)
对每一个空格求出初始状态下所能填的所有数字,并放入它所对应的set中
(3)int removeItem(int x, int y, int xx, int yy)
在(x,y)上填上假想的数字后去更新空格(xx,yy)所对应的可填数字集合
(4)bool dfsSolve(vector<Node> emptyPos)
找到当前状态下可填数最少的空格,调用removeItem函数对其它空格可填数集合进行更新,并调用dfsSolve函数递归求解问题
(5)void solve()
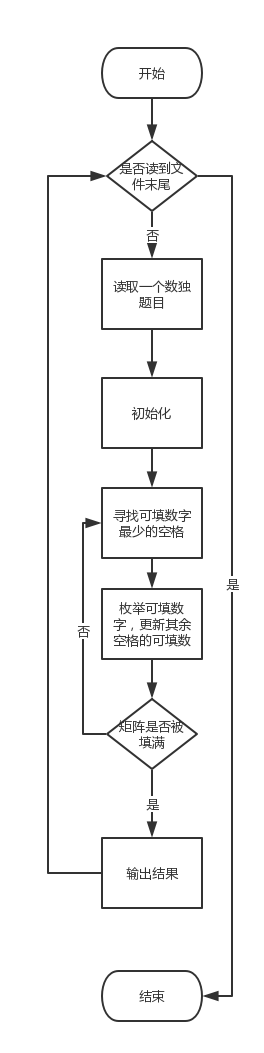
解决问题的入口,负责读入数据(scanf),并调用相应的函数(init,initSetOfThisEmptyPos)给数据结构赋上初值,调用dfsSolve函数进行递归求解
DLX:解决精确覆盖问题
其中包含六个函数,分别是:
(1)void init(int n)
初始化链表和记录每一列节点个数的数组S以及一些变量
(2)void addRow(int r, int columns[], int cnt)
添加一行节点到链表里
(3)void remove(int c)
移除节点标号为c所在的列,并删除相应的行
(4)void void restore(int c)
恢复节点标号为c所在的列,并恢复相应的行
(5)bool dfs(int d)
调用dfs函数递归求解问题,调用remove函数删除列,调用restore函数恢复对应列
(6)bool solve(int ansRe[], int &ansSize)
解决问题的入口,负责调用dfs函数递归求解并返回求出来的结果到ansRe中
SolveS_DLX:用DLX算法解决求解数独问题
其中包含三个函数,分别是:
(1)int encode(int a, int b, int c)
给决策(a,b,c)编码
(2)void decode(int code, int &a, int &b, int &c)
将编码解码成决策(a,b,c)
(3)void solve()
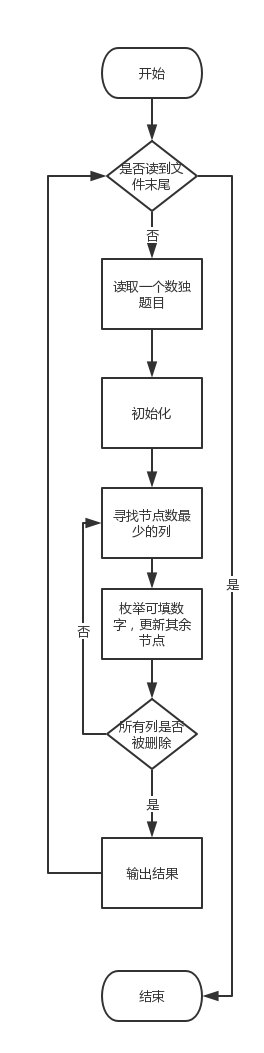
解决问题的入口,负责读入数据(scanf),调用solver.init函数初始化DLX链表,调用solver.addRow函数添加一行节点,调用encode函数给决策编码,调用solver.solve函数求解问题,调用decode函数解码,通过output函数将结果输出到文件
流程图
SolveC.solve():
SolveS.solve():
SolveS_DLX.solve():
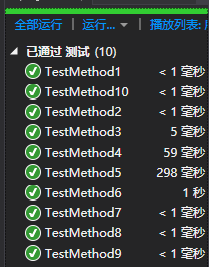
单元测试
单元测试中需要实现相应函数来判断一个数独终局是否合法,并对-c参数和-s参数分别测试代码正确性。由于最后还是决定交DLX算法,于是把暴力的结构体代码全部注释掉了。
TEST_METHOD(TestMethod1)
{
SolveC solveC;
int a[matrixLen];
solveC.initPermutation(a);
//Assert::AreEqual(a[matrixLen-1],firstNum);
}
TEST_METHOD(TestMethod2)
{
SolveC solveC;
solveC.n = 2;
solveC.rowChange(3);
Assert::AreEqual(solveC.n, 0);
}
TEST_METHOD(TestMethod3)
{
SolveC solveC;
solveC.n = 200;
solveC.solve();
Assert::AreEqual(solveC.n, 0);
Assert::AreEqual(checkMatrix(solveC.newSeed), true);
}
TEST_METHOD(TestMethod4)
{
SolveC solveC;
solveC.n = 2000;
solveC.solve();
Assert::AreEqual(solveC.n, 0);
Assert::AreEqual(checkMatrix(solveC.newSeed), true);
}
TEST_METHOD(TestMethod5)
{
SolveC solveC;
solveC.n = 10000;
solveC.solve();
Assert::AreEqual(solveC.n, 0);
Assert::AreEqual(checkMatrix(solveC.newSeed), true);
}
TEST_METHOD(TestMethod6)
{
SolveS_DLX solveS;
freopen("C:/Users/acer-pc/Desktop/git/softwareFirstHomework/sudoku/sudoku/1.in", "r", stdin);
solveS.solve();
Assert::AreEqual(checkMatrix(solveS.matrix), true);
}
TEST_METHOD(TestMethod7)
{
SolveS_DLX solveS;
Assert::AreEqual(solveS.encode(2,4,8),207);
}
TEST_METHOD(TestMethod8)
{
SolveS_DLX solveS;
int a, b, c;
solveS.decode(207,a,b,c);
Assert::AreEqual(a, 2);
Assert::AreEqual(b, 4);
Assert::AreEqual(c, 8);
}
TEST_METHOD(TestMethod9)
{
DLX solve;
solve.init(5);
Assert::AreEqual(solve.sz,6);
}
TEST_METHOD(TestMethod10)
{
Assert::AreEqual(firstNum,1);
}
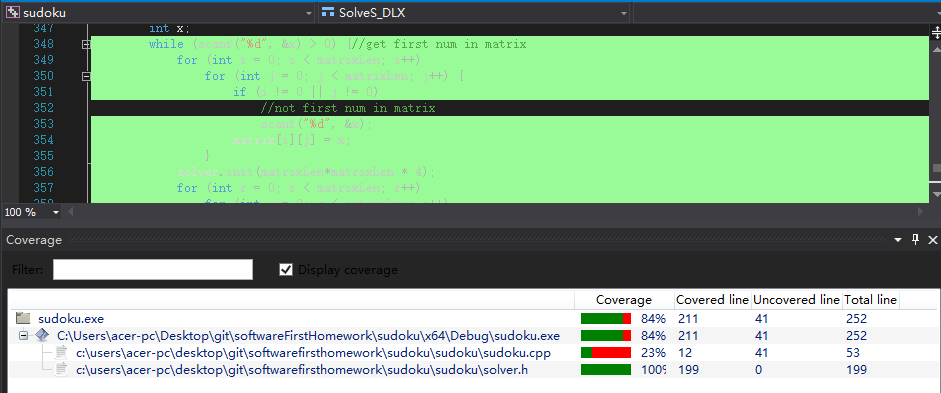
覆盖率分析
可以看到实现功能的头文件solver.h的覆盖率为百分之百
性能分析与代码改进
设置参数为 “-c 1000000”
第一次运行的耗时为27.509秒
可见耗时最多的函数是output函数,output函数里我用putchar()函数逐个字符输出。
我把输出函数单独提出来在VS上新建项目并测试,发现耗时为19.035秒。我换了个IDE平台进行测试,发现只需要1.931秒
无奈把输出方式成了fputs输出,运行耗时变为了15.243秒
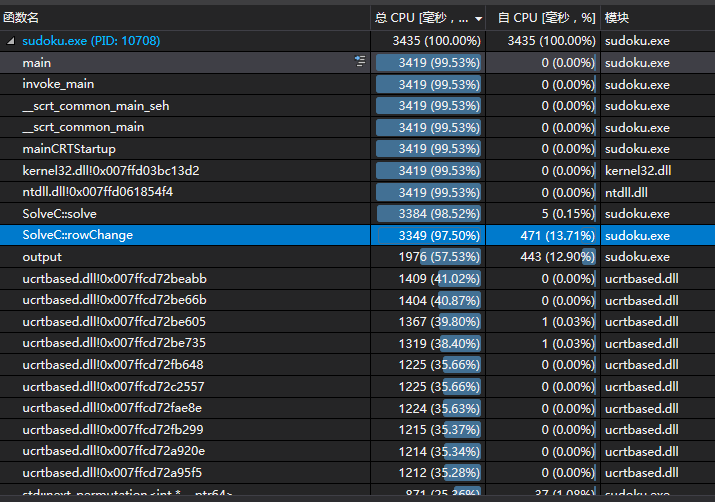
貌似还是不够快,从上图我们可以看出swap()函数是相当费时的。
找到用到swap函数的地方,改成了手写的交换元素,程序跑得更快了,耗时3.435秒
设置参数为 “-s 1.in”
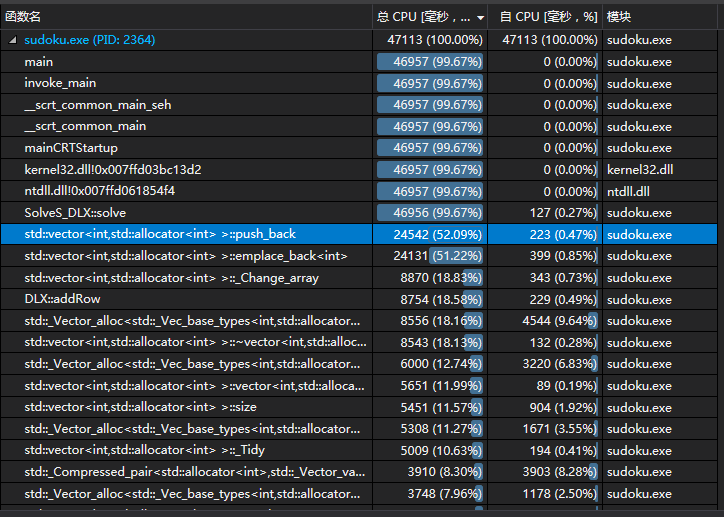
1.in中有4000组随机数据,第一次运行的耗时为47.113秒
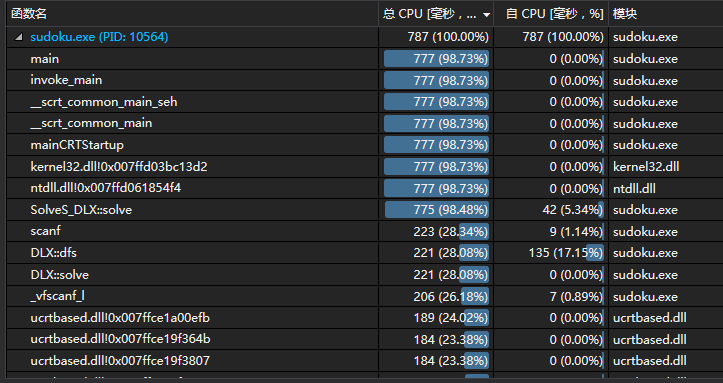
从上图可以看出vector的push_back相当耗时,于是我尝试着把vector全部替换为数组。哇,太神奇了,尽然只需要0.787秒!
代码说明
const int seed[matrixLen][matrixLen] = {
{ 1, 2, 3, 4, 5, 6, 7, 8, 9 },
{ 4, 5, 6, 7, 8, 9, 1, 2, 3 },
{ 7, 8, 9, 1, 2, 3, 4, 5, 6 },
{ 2, 1, 4, 3, 6, 5, 8, 9, 7 },
{ 3, 6, 5, 8, 9, 7, 2, 1, 4 },
{ 8, 9, 7, 2, 1, 4, 3, 6, 5 },
{ 5, 3, 1, 6, 4, 2, 9, 7, 8 },
{ 6, 4, 2, 9, 7, 8, 5, 3, 1 },
{ 9, 7, 8, 5, 3, 1, 6, 4, 2 }
};
进行变换前需要一个正确的数独种子,从网上获得
void rowChange(int row) {
if (row >= matrixLen) {
output(newSeed);
n--;
return;
}
int per[3];
for (int i = 0; i < 3; i++)
per[i] = row + i;
do {
int temp[3][matrixLen];
for (int i = row; i < row + 3; i++) {
memcpy(temp[i % 3], newSeed[per[i % 3]], sizeof(temp[0]));
}
for (int i = row; i < row + 3; i++) {
swap(temp[i % 3], newSeed[i]);
}
rowChange(row + 3);
if (!n)
return;
for (int i = row; i < row + 3; i++) {
swap(temp[i % 3], newSeed[i]);
}
} while (next_permutation(per, per + 3));
}
行从0开始标号,这是对3,4,5和6,7,8行的变换从而生成新的数独
while (n > 0) {
for (int i = 0; i < matrixLen; i++)
for (int j = 0; j < matrixLen; j++) {
newSeed[i][j] = trans[numToPos[seed[i][j]]];
}
rowChange(3);
if (!n)
break;
swap(newSeed[1], newSeed[2]);
rowChange(3);
next_permutation(trans, trans + matrixLen - 1);
}
对每个种子,都采用行变换来生成新的数独,通过algorithm库中的next_permutation函数来生成下一个全排列
void addRow(int r, int columns[], int cnt) {
//r 行号,columns存放这一行的哪些列为1
int first = sz;//sz 当前新建节点标号
for (int i = 0; i < cnt; i++) {
int c = columns[i];
L[sz] = sz - 1;
R[sz] = sz + 1;
D[sz] = c;
U[sz] = U[c];
D[U[c]] = sz;
U[c] = sz;
row[sz] = r;
col[sz] = c;
S[c]++;
sz++;
}
R[sz - 1] = first;
L[first] = sz - 1;
}
往DLX的链表中添加一行节点,修改对应的指针(这里是数组模拟链表)
#define FOR(i,A,s) for(int i= A[s];i!=s;i=A[i])
顺着链表A,遍历除s外的其它元素
void remove(int c) {
L[R[c]] = L[c];
R[L[c]] = R[c];
FOR(i, D, c)
FOR(j, R, i) {
U[D[j]] = U[j];
D[U[j]] = D[j];
--S[col[j]];
}
}
移除标号为c的节点所在的列
void restore(int c) {
//恢复标号c所在的列
FOR(i, U, c)
FOR(j, L, i) {
++S[col[j]];
U[D[j]] = j;
D[U[j]] = j;
}
L[R[c]] = c;
R[L[c]] = c;
}
恢复标号c所在的列,注意恢复的顺序与移除的顺序相反
int encode(int a, int b, int c) {
return (a * matrixLen + b) * matrixLen + c + 1;
}
将决策(a,b,c)进行编码,映射到对应的行号上
void decode(int code, int &a, int &b, int &c) {
code--;
c = code%matrixLen;
code /= matrixLen;
b = code %matrixLen;
code /= matrixLen;
a = code;
}
将code解码获得决策(a,b,c),用于获得答案矩阵
for (int r = 0; r < matrixLen; r++)
for (int c = 0; c < matrixLen; c++)
for (int v = 0; v < matrixLen; v++) {
if (matrix[r][c] == 0 || matrix[r][c] == v + 1) {
int columns[10];
int cnt = 0;
//列号从1开始
columns[cnt++] = encode(SLOT, r, c);
columns[cnt++] = encode(ROW, r, v);
columns[cnt++] = encode(COL, c, v);
columns[cnt++] = encode(SUB, r / 3 * 3 + c / 3, v);
solver.addRow(encode(r, c, v), columns, cnt);
}
}()
枚举决策(r,c,v),向链表中逐行添加节点,每个决策对应四个可满足的条件(SLOT,ROW,COL,SUB)
表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 60 | 30 |
| · Estimate | · 估计这个任务需要多少时间 | 60 | 30 |
| Development | 开发 | 5700 | 2820 |
| · Analysis | · 需求分析 (包括学习新技术) | 480 | 360 |
| · Design Spec | · 生成设计文档 | 480 | 180 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 360 | 60 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 60 | 60 |
| · Design | · 具体设计 | 360 | 240 |
| · Coding | · 具体编码 | 1800 | 1200 |
| · Code Review | · 代码复审 | 360 | 120 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 1800 | 600 |
| Reporting | 报告 | 360 | 420 |
| · Test Report | · 测试报告 | 120 | 120 |
| · Size Measurement | · 计算工作量 | 120 | 120 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 120 | 180 |
| 合计 | 6120 | 3270 |
GUI展示
采用QT+VS2017开发
程序一开始随机生成数独题目,玩家可以用鼠标点击挖空的地方,用键盘输入数字。点击submit按钮即可提交自己的答案。在按钮旁边会显示文字提示玩家的答案是否正确。真是太好玩了,赶紧叫上小伙伴们一起哈皮吧!



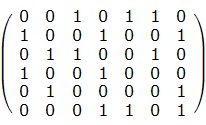




 浙公网安备 33010602011771号
浙公网安备 33010602011771号