空间向量在任意平面的投影公式推导 (矩阵方法)
若 V是Rn 的一个子空间,已知V的一组基向量 {b1, b2, b3,... bk}
则: ![]()
可构建矩阵 :A(nxk) = {b1 b2 b3 b4...bn}
有:![]()
x(m,n,q) 为空间向量
矩阵 A 包含平面的基向量 A(3x3)
根据投影的定义有 :
原向量 - 投影向量 = 投影向量的正交补
![]() (1)
(1)
![]() (2)
(2)
又根据投影定义, 投影向量的正交补 垂直 投影平面的子空间,则根据 (1) (2) 得到
![]() (3)
(3)
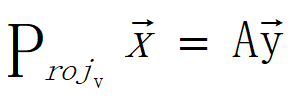 (4)
(4)
由(3) (4) 可得:
![]()
则,投影向量为:
![]()
只需要代入平面的基向量,以及 x , 可以求得该向量在这个平面的投影向量。



