基于OTSU（大津法）和图像分块的阈值分割

概述：OSTU又叫大津法, 由日本学者大津于1979年提出

　　—从大津法的原理上来讲，该方法又称作最大类间方差法，因为按照大津法求得的阈值进行图像二值化分割后，前景与背景图像的类间方差最大。

　　—它是按图像的灰度特性，将图像分成背景和前景两部分。因方差是灰度分布均匀性的一种度量, 背景和前景之间的类间方差越大,说明构成图像的

两部分的差别越大, 当部分前景错分为背景或部分背景错分为前景都会导致两部分差别变小。因此, 使类间方差最大的分割意味着错分概率最小。

 

算法原理：

其中：

 

 

算法基本步骤：

 

 

 

不足之处：大津法对于背景灰度比较均衡的图片处理效果确实比较好，但是对于

背景灰度不均衡的图片而言，效果不太好。

 

 

处理灰度相对均衡的图片效果图：

 

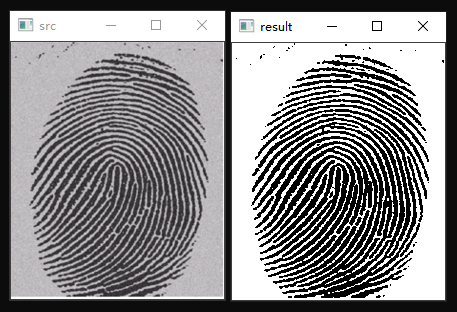
处理背景灰度不均衡的图片效果图：

 

 

 解决方案，对于灰度不均衡的图片，将图片进行分块求阈值处理，

然后求出的阈值对该块图片进行二值化处理，再将二值化之后的

部分图片写入到新的一张图片中。

 

基于OTSU和分块处理后阈值分割效果图，分割成8块：

 

 

 

 源码：

//基于OTSU求图像最佳分割阈值
int CalcThreshold(cv::Mat src)
{
	int threshold = 0;				//需要求的阈值
	long grayData[256] = { 0 };		//出现的灰度级的次数
	double probData[256] = { 0 };	//概率数组

	for (int i = 0; i < src.rows; i++)
	{
		uchar* src_rows_ptr = src.ptr<uchar>(i);
		for (int j = 0; j < src.cols; j++)
		{
			grayData[src_rows_ptr[j]]++;		//统计灰度值的次数，下标代表灰度级0~255，数组值代表次数

		}
	}

	for (int i = 0; i < 256; i++) {
		probData[i] = (double)grayData[i] / (src.rows*src.cols);	//求灰度在全图出现的概率
	}

	double p1, p2, m1, m2, sigma=0.,temp;


			for (int i = 0; i < 256; i++) {
				p1 = p2 = m1 = m2 = temp = 0;
				for (int j = 0; j < 256; j++) {
					if (j <= i) {
						p1 += probData[j];
						m1 += probData[j]*j;
					}
					else {
						p2 += probData[j];
						m2 += probData[j]*j;
					}
				}
				m1 /= p1;
				m2 /= p2;
				temp = p1 * p2*(m1 - m2)*(m1 - m2);
				if (sigma < temp) {
					sigma = temp;
					threshold = i;			//求最大差值的阈值，此阈值为最好分割阈值
				}
			}
	return threshold;
}

　　

 

//将图片分块，求阈值，再将图片写入一张大图片中
void Devide(cv::Mat src, int rowBlock, int colBlock)
{
	int count = 0;

	Mat result = Mat::zeros(Size(src.cols,src.rows), src.type());
	Mat tmp = Mat::zeros(Size(src.cols / colBlock, src.rows / rowBlock), src.type());
	for (int x = 0, xx = src.cols-colBlock; x < xx; x += (src.cols / colBlock)) {
		for (int y = 0, yy = src.rows-rowBlock; y < yy; y += (src.rows/ rowBlock)) {

			tmp = src(Rect(x, y, (src.cols /colBlock), (src.rows/rowBlock)));

			count++;
			int thresTh = CalcThreshold(tmp);
			cv::threshold(tmp, tmp, thresTh, 255, THRESH_BINARY);


			tmp.copyTo(result(Rect(x, y, tmp.cols, tmp.rows)));
		}
	}
	imshow("result", result);
}