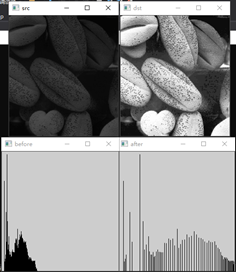
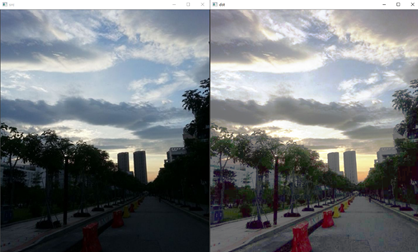
直方图均衡
直方图均衡
一、目的与原理
(1)目的:增加图像的全局对比度
(2)原理:直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。直方图均衡化就是对图像进行非线性拉伸,重新分配图像像素值,使一定灰度范围内的像素数量大致相同,实际上就是使得图片的亮暗程度增加使比较密集的灰度向两侧扩散。

公式①:

(L-1)是灰度范围,T(rk)是累积分布函数,Pr(rj)是概率密度
二、步骤
(1)得到原始图片的灰度直方图
(2)得到各个灰度级对应的概率密度函数
(3)通过概率密度函数得到累积分布函数
(4)累计分布函数乘以255,得到每一个灰度级对应的新的灰度
(5)通过第4步的结果,将旧灰度映射得到新的灰度,即更新整张图片的灰度
三、特点
直方图均衡化的缺点
如果一幅图像整体偏暗或者偏亮,那么直方图均衡化的方法很适用。但直方图均衡化是一种全局处理方式,它对处理的数据不加选择,可能会增加背景干扰信息的对比度并且降低有用信号的对比度(如果图像某些区域对比度很好,而另一些区域对比度不好,那采用直方图均衡化就不一定适用)。此外,均衡化后图像的灰度级减少,某些细节将会消失;某些图像(如直方图有高峰),经过均衡化后对比度不自然的过分增强。针对直方图均衡化的缺点,已经有局部的直方图均衡化方法出现。
四、源码
//直方图均衡化
Mat Histogramequalization(Mat src) {
int R[256] = { 0 };
int G[256] = { 0 };
int B[256] = { 0 };
int rows = src.rows;
int cols = src.cols;
int sum = rows * cols; //分辨率
//统计直方图的RGB分布
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
B[src.at<Vec3b>(i, j)[0]]++;
G[src.at<Vec3b>(i, j)[1]]++;
R[src.at<Vec3b>(i, j)[2]]++;
}
}
//构建直方图的累计分布方程,用于直方图均衡化
double val[3] = { 0 };
for (int i = 0; i < 256; i++) {
val[0] += B[i]; //val[0]是红色出现的累积频率
val[1] += G[i]; //val[1]是红色出现的累积频率
val[2] += R[i]; //val[2]是红色出现的累积频率
B[i] = val[0] * 255 / sum; //B[0~255]
G[i] = val[1] * 255 / sum;
R[i] = val[2] * 255 / sum;
}
//归一化直方图
Mat dst(rows, cols, CV_8UC3);
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
dst.at<Vec3b>(i, j)[0] = B[src.at<Vec3b>(i, j)[0]];
dst.at<Vec3b>(i, j)[1] = G[src.at<Vec3b>(i, j)[1]];
dst.at<Vec3b>(i, j)[2] = R[src.at<Vec3b>(i, j)[2]];
}
}
return dst;
}
Mat Histogramequal(Mat src) {
int arr[256] = { 0 };
int rows = src.rows;
int cols = src.cols;
int sum = rows * cols;
//统计直方图的RGB分布
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
arr[src.at<uchar>(i, j)]++;
}
}
//构建直方图的累计分布方程,用于直方图均衡化
double val[3] = { 0 };
for (int i = 0; i < 256; i++) {
val[0] += arr[i];
arr[i] = val[0] * 255 / sum;
}
//归一化直方图
Mat dst(rows, cols, CV_8UC1);
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
dst.at<uchar>(i, j) = arr[src.at<uchar>(i, j)];
}
}
return dst;
}
五、结果图