力扣-46-全排列

回溯法模板题

回溯法

感觉这个方法的题目都比较难，全是中等

回溯算法本质上是对深度优先遍历DFS的优化，当已经到达终点/已经没有可以选择（选择都访问过了）的时候，，就向上回退一步
这里引入了一个概念叫“状态”——每一个节点表示了求解问题的不同阶段，而每一次回溯都需要“重置状态”（这在算法中的体现通常是一个方法）

class Solution {
    // 解题思路：看作是填从左往右n个空格
public:
// 递归函数
// 参数：用于保存结果的二维数组、当前排列数组、从左往右第first个位置、单个结果数组长度（即题目给的可用数字数组的长度）
    void backtrack(vector<vector<int>>& res, vector<int>& output, int first, int len){
        // 当已经填到最后一个位置，则将这个结果数组放入二维数组中
        if (first == len) {
            res.emplace_back(output);
            return;
        }
        for (int i = first; i < len; ++i) {
            // 这个first在for循环中是不会变的，一直都是层数——也可以说是要填的第几个位置
            // 动态维护数组，把选中的换到左边去
            // first是一个从左到右递增的固定位置，将当前的操作位置与之互换后，当前位置就是本次选择的元素，当前位置（包括）之前都是已经选过的，之后都是没有选过的
            swap(output[i], output[first]);
            // 继续递归填下一个数
            backtrack(res, output, first + 1, len);
            // 撤销操作，因为下面的可能性都跑完了，要恢复output数组以供下一次for循环使用
            swap(output[i], output[first]);
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int> > res;
        backtrack(res, nums, 0, (int)nums.size());
        return res;
    }
};

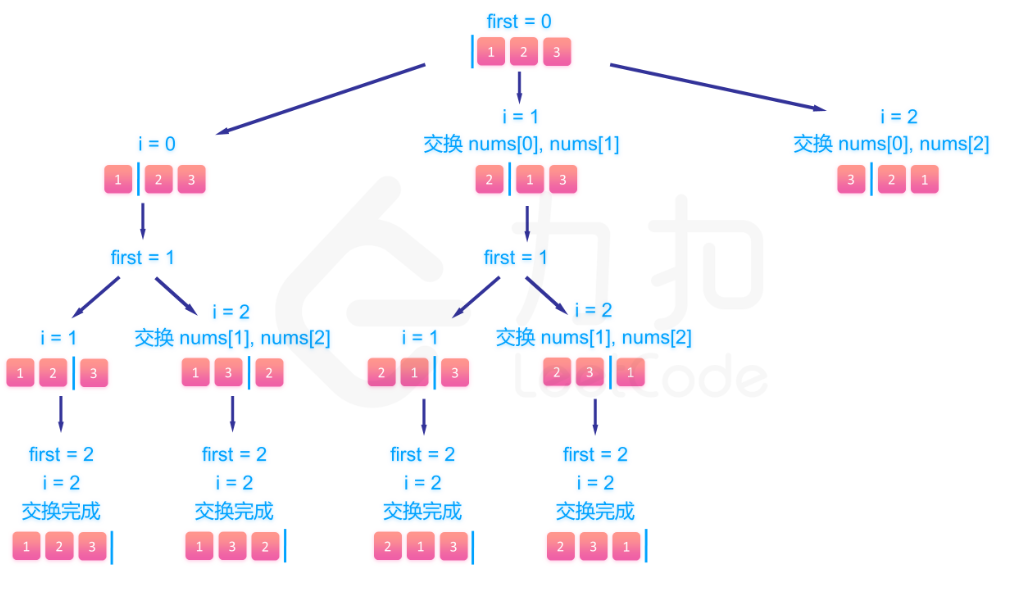
百思不得其解的是这两个相同的交换步骤是什么意思
题解的说法是说把数组分成两个部分，左边是已经填过，右边是待填的数，然后这两步就是维护这个数组的

还有就是这个for循环和递归
递归过程应该是填一个序列的

更新

	vector<vector<int>> res;
	vector<vector<int>> permute(vector<int>& nums) {
		res.clear();
		backtrack(nums, 0, nums.size());
		return res;
	}
 
	// index表示当前填的位置，temp是当前的排列
	void backtrack(vector<int> &temp,int index,int len) {
		if (index == len) {
			// 当要填的位置都填满了
			res.push_back(temp);
			return;
		}
		// 按理说这里应该是遍历nums，从中选出一个放入新数组并标记原数组中的元素
		// 但这这里采用了交换的做法，省去了步骤，将选中的元素与index位置的元素交换
		// index（包括），左边是已经排好的，右边是还可以选择的
		for (int i = index; i < len; i++) {
			swap(temp[index], temp[i]);
			backtrack(temp, index + 1, len);
			swap(temp[index], temp[i]);
			// 是这样的，每一次for循环相当于选一个元素放到指定位置，然后递归去填下一个位置
			// 为了不影响当前位置填别的元素，所以这里要换回来
		}
	}

这次再看确实是能够自己想明白了
值得一提的是，这里用了全局结果数组变量+每次执行方法清空的写法，虽然我也不确定这样是不是一定比每次创建一个局部二维数组效率高，但是每次传参真的挺麻烦，但话又说回来，传的也只是个引用

另外就是，写出它所有的非空子排列，例如对于[1,2,3]
[1,2,3],[2,1,3],[3,1,2],[1,3,2],[2,3,1],[3,2,1]
[1,2],[2,1],[1,3],[2,3],[3,1],[3,2]
[1],[2],[3]

其实按理来说这里backtrack(nums, 0, nums.size());改改第三个参数就行，但事实上没法这么干，应为上面的代码为了全排列做了特殊优化——也就是用交换来代替临时数组，也就是不管处理几位，这里插入的都是3个数字的数组

啊，我发现这个问题还真不是那么简单

看这道题力扣491-递增子序列