力扣-53-最大子数和

53-最大子数和

2022/10/29 重做

dp数组定义为：以i结尾的子数组的最大和

这样相对于定义为：前i个元素的最大子数和同样能做到全覆盖（但是这样没办法保证连续，子序列或许能这么用）

状态转移方程为：

• 如果f(i-1)<0，则对最大字数和无贡献，f(i) = nums[i]
• 如果f(i-1)>0，则f(i) = f(i-1)+nums[i]

那为什么不是判断nums[i]是否大于零，而是判断f(i)？
因为为了保证子数组连续（而且定义中也说了是最后一个），nums[i]一定存在于结果中

那么考虑下初始化的问题，dp数组只跟前一个元素有关，所以只需要初始化1个
为了保证dp[1]的值=nums[0]，需要把dp[0]初始化为0，这样无论是那种情况对结果都没有影响

另外这里注意，这样得出的dp数组，dp[n]只代表了以n结尾的子数组最大值，而不是整个数组中的最大值，所以这里需要一个额外的变量来保存最大值

最大子数组不一定是以最后一个元素结尾的

int maxSubArray(vector<int>& nums) {
	// 数组中有正有负
	int n = nums.size();
	vector<int> dp(n + 1,0);
	int maxSum =-101;// nums[i]最小值100
	for (int i = 1; i <= n; i++) {
		if (dp[i - 1] < 0) dp[i] = nums[i - 1];
		else dp[i] = dp[i - 1] + nums[i - 1];
		maxSum = max(maxSum, dp[i]);
	}

	return maxSum;
}

还可以把if-else去掉

int maxSubArray(vector<int>& nums) {
	int n = nums.size();
	vector<int> dp(n + 1,0);
	int maxSum =-101;
	for (int i = 1; i <= n; i++) {
		dp[i] = max(nums[i - 1], dp[i - 1] + nums[i - 1]);
		maxSum = max(maxSum, dp[i]);
	}
	return maxSum;
}

---

本来按照《剑指Offer》42：连续子数组的最大和 给出的状态转移方程提示写出了第一版

        int maxSubArray(vector<int>& nums) {
        int len = nums.size();
        vector<int> result(len);
        result[0] = nums[0];
        int maxSum = result[0];
        for (int i = 1; i < len; ++i) {
            if (result[i - 1] < 0) {
                result[i] = nums[i];
            }
            else {
                result[i] = nums[i] + result[i - 1];
            }
            maxSum = max(result[i], maxSum);
            // result数组中保存的应该是，加到每一步的子数组和（抛弃了和为负的元素）
            // 那么还需要一个来保存最大的子数组和
        }
        return maxSum;

然后转念一想，可以就在原数组上操作，而不必新声明一个数组，也算是降低空间复杂度的优化

        int maxSum = nums[0];
        for(int i = 1;i<nums.size();++i){
            if(nums[i-1]>0){
                nums[i]+=nums[i-1];
        // 至少累加两个元素，如果结果<0，即对后面的和贡献为负，舍弃 
            }
            maxSum = max(nums[i],maxSum);
        // maxSum用于比较并保存最大和
        }
        return maxSum;

结果时间复杂度惨不忍睹😂

可能我哪里思路得不够好，还有更好的解法也是肯定的，但有没有一种可能——动态规划的解题思路本来开销就比较大

2023/2/22

	int maxSubArray(vector<int>& nums) {
		int maxSum = nums[0], pre = nums[0], cur;
		// dp[i]表示以i位置结尾的最大子数和
		// 因为是结尾，所以本身一定存在，同时又能够覆盖所有情况
		// 如果dp[i]<=0，那么对最大子数组的和是没有贡献（负贡献）
		for (int i = 1; i < nums.size(); i++) {
			if (pre < 0) cur = nums[i];
			else cur = nums[i] + pre;
			pre = cur;
			maxSum = max(maxSum, cur);
		}
		return maxSum;
	}

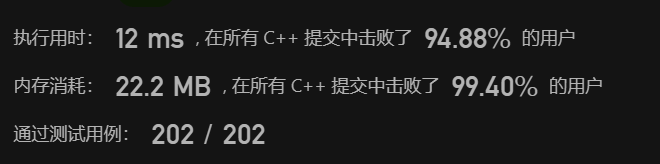
空间优化，使用两个常量来替代数组，效果很棒
注意这里的 pre 不能和 maxSum 合并，不能被“优化掉”