acm数论之矩阵快速幂+快速幂
一.取模运算的性质:
(1)(a+b)%c=(a%c+b%c)%c
(2)(ab)%c=(a%c)(b%c)%c
快速幂的复杂度分析:o(log n)
快速幂的原理
采用位运算的两种工具:
&:这里用作分析数的奇偶性,x&1==1数为奇数,x&1==0数为偶数
>>:这里是二进制的所有位向右移一位,一般可以看作是log(2) n,但是与直接以2为底数取对数不同,比如数1,所得到的结果完全不同,所以我们这直接使用位运算>>更合适。
运用矩阵相乘的相关知识:
两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵,它们的乘积C是一个m×p矩阵
![]() 它的一个元素:
它的一个元素:
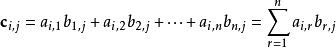
例如:
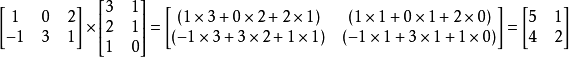
1 juzh chengfa(juzh kk,juzh ll) 2 { 3 juzh result; 4 memset(result.a,0,sizeof(result.a)); 5 for(int i=0;i<len;i++) 6 for(int j=0;j<len;j++) 7 for(int h=0;h<len;h++) 8 result.a[i][j]=(result.a[i][j]+kk.a[i][h]*ll.a[h][j])%mmod; 9 return result; 10 }
快速幂就是采用二分思想快速取幂
a^b=a*a*a*...
分析b:
如果b为偶数:a^b=a^(b/2*2)=a^(b/2)*a^(b/2)
如果b为奇数:a^b=a*a^((b-1)/2*2)=a*a^(b-1/2)*a^(b-1/2)
这里我们只讨论二分一次的结果:我们可以看出来原本的a^b变成了a^(b/2)^2,如果这时使用暴力法,我们只需进行(for(int i=1;i<=n/2;i++),一下子减少了一半。
后面继续二分,直到b分为1,操作次数差不多是o(log n)
快速幂的关键代码
1 long long solve(int a,int b,int mod) 2 { 3 long long ans=1; 4 while(b!=0)//b>0 5 { 6 if(b&1)//说明b为奇数,分成a*ans 7 ans=(ans*a)%mod; 8 a=a*a; 9 b>>=1; 10 } 11 return ans; 12 }
快速幂适合解决的问题
1、快速幂取模(a^b) mod (m)(a,b都是非常大的数据时)---减少时间复杂度
算法的原理是a^b mod c=(a mod c)(b mod c)mod c
在面对a^b(a,b都是非常大的数据时)时,假如使用暴力法(即for(int i=1;i<=n;i++)a*=a;),很明显复杂度为o(n)
而采用了二分思想的快速幂,复杂度为o(logn)
注明:快速幂和暴力法一样当数据过大如果数据不进行取模这一步骤时,数据很有可能溢出,但是快速幂的优势在于复杂度低,所用时间快
2.矩阵快速幂
#include<iostream> #include<algorithm> #include<string> #include<string.h> using namespace std; int n,m;//m即mod struct node{ int a[35][35]; }; node ONE; node multi(node X,node Y)//X*Y矩阵相乘 { node R; for(int i=0;i<n;i++) for(int j=0;j<n;j++) { R.a[i][j]=0; for(int k=0;k<n;k++) R.a[i][j]=(R.a[i][j]+X.a[i][k]*Y.a[k][j])%m; } return R; } node add(node X,node Y)//X+Y矩阵相加 { node R; for(int i=0;i<n;i++) for(int j=0;j<n;j++) { R.a[i][j]=(X.a[i][j]+Y.a[i][j])%m; } return R; } node factorial(node X,int t)//X矩阵的t次方 { node ans; memset(ans.a,0,sizeof(ans.a)); for(int j=0;j<n;j++)//初始化为单位矩阵 ans.a[j][j]=1; while(t!=0) { if(t&1) ans=multi(ans,X); X=multi(X,X); t>>=1; } return ans; }
可以解决f(n)与f(n-1)类的式子的计算
例如:
题目要求:f(n)=2*f(n-1)+1(n为奇数)f(n)=2*f(n-1)(n为偶数),f(0)=0,1<=n, m <= 1000000000;输入n,m(模)求出f(n)mod m的值
分析题目:n>=1,m>=1000000000;如果直接暴力,结果一定是超时
这类题目采用矩阵快速幂的方法进行解决。
假设幂矩阵为kk,答案矩阵(包含题中所求的f[n])为ans,过渡矩阵(即包含f[n-1]的矩阵)为hh
构造矩阵数学式:
注意我们只讨论偶数(使用偶数方便,n/2=1,2,3...)构造矩阵求解,奇数的结果可以看成上一个数*2+1
分析题目数据:1,2,5,10,21,42,可以知道偶数规律:f1(s)=4*f1(s-1)+2;(注意这里是单拿出来偶数,s=n/2,n=2的数据f(2)是s=1的f1(1)
kk*hh=ans;
4 2 f[n-1] f[n]
0 1 1 1
(ps:学习矩阵快速幂前需要了解两矩阵如何相乘等基础操作)
4 2 f[n-2] f[n-1]
0 1 1 1
这个kk矩阵的n次方,kk^n*hh=ans,f[n]=ans.a[0][0];hh= 0
4 1 f[0] f[n] 1
0 1 1 1
解决代码:

1 #include<iostream> 2 #include<string> 3 #include<string.h> 4 using namespace std; 5 #define len 2 6 int mmod; 7 struct juzh{ 8 long long a[len][len]; 9 }; 10 juzh chengfa(juzh kk,juzh ll) 11 { 12 juzh result; 13 memset(result.a,0,sizeof(result.a)); 14 for(int i=0;i<len;i++) 15 for(int j=0;j<len;j++) 16 for(int h=0;h<len;h++) 17 result.a[i][j]=(result.a[i][j]+kk.a[i][h]*ll.a[h][j])%mmod; 18 return result; 19 } 20 long long solve(juzh kai,int b)//a^b%mod 21 { 22 juzh ans;//ans为单位矩阵 23 ans.a[0][0]=1; 24 ans.a[0][1]=ans.a[1][0]=0; 25 ans.a[1][1]=1; 26 while(b!=0)//b>0 27 { 28 if(b&1) 29 ans=chengfa(ans,kai); 30 kai=chengfa(kai,kai); 31 b>>=1; 32 } 33 return ans.a[0][1]; 34 } 35 //这里需要注意分开偶数与奇数 36 int main() 37 { 38 int n; 39 while(cin>>n>>mmod) 40 { 41 juzh kai; 42 kai.a[0][0]=4,kai.a[0][1]=2,kai.a[1][0]=0,kai.a[1][1]=1; 43 if(n&1)//说明为奇数 44 cout<<(solve(kai,(n-1)/2)*2+1)%mmod<<endl; 45 else 46 cout<<solve(kai,n/2)<<endl; 47 } 48 }
采用矩阵快速幂方法的步骤:
1.构建kk幂矩阵,ans矩阵,hh过渡矩阵
2.幂矩阵与初始ans矩阵乘n次(ans矩阵初始化是单位矩阵:ans[i][i]=1)
3.kk^n*E(E为单位矩阵)*hh=ans,分析ans,根据矩阵相乘相关知识得出f(n)
3.求取大数的后k位
例题:lightoj 1282 Leading and Trailing

1 #include <cstdio> 2 #include<algorithm> 3 #include<string.h> 4 #include<string> 5 #include<algorithm> 6 int MOD; 7 struct Matrix 8 { 9 long long a[2][2];//幂矩阵的大小 10 Matrix () {} 11 Matrix operator * (Matrix const &b)const 12 { 13 Matrix res; 14 memset(res.a,0,sizeof(res.a)); //矩阵相加 a[i][j]=sum(b[i][k]+c[k][j]); 15 for (int i = 0; i < 2; i++)//a.x即i 16 for (int j = 0; j < 2; j++) //a.y即j 17 for (int k = 0; k < 2; k++) //b.y即k 18 res.a[i][j] = (res.a[i][j] + this->a[i][k] * b.a[k][j]) % MOD; 19 return res; 20 } 21 }; 22 Matrix pow_mod(Matrix base, int n) 23 { 24 Matrix ans; 25 memset(ans.a,0,sizeof(ans.a));//设置ans的初始矩阵值 26 ans.a[0][0] = ans.a[1][1]=1; 27 while (n > 0) 28 { 29 if (n & 1) 30 ans = ans * base; 31 base = base * base; 32 n >>= 1; 33 } 34 return ans; 35 } 36 int main() 37 { 38 Matrix base;//设置幂矩阵的值 39 base.a[0][0] = 1; 40 base.a[0][1] = 1; 41 base.a[1][0] = 1; 42 base.a[1][1] = 0; 43 int n; 44 while (~scanf("%d%d", &n, &MOD)) 45 { 46 Matrix ans = pow_mod(base, n);//得到存放f[n]的矩阵 47 printf("%d\n",ans.a[1][0]);// f[n]存放在ans矩阵中的a[1][0]这个位置(看具体自己设的矩阵公式) 48 } 49 } 50 51 poj 3070

1 #include<iostream> 2 #include<algorithm> 3 using namespace std; 4 struct node{ 5 long long a[2][2]; 6 }; 7 long long m1; 8 node chengfa(node m,node n) 9 { 10 node k; 11 for(int i=0;i<2;i++) 12 for(int j=0;j<2;j++) 13 k.a[i][j]=0; 14 for(int i=0;i<2;i++) 15 for(int j=0;j<2;j++) 16 for(int k1=0;k1<2;k1++) 17 k.a[i][j]=(k.a[i][j]+m.a[i][k1]*n.a[k1][j])%m1; 18 return k; 19 } 20 node solve(node m,int n) 21 { 22 node ans; 23 ans.a[0][0]=ans.a[1][1]=ans.a[1][0]=0; 24 ans.a[0][1]=1; 25 while(n>0) 26 { 27 if(n&1!=0) 28 ans=chengfa(ans,m); 29 m=chengfa(m,m); 30 n>>=1; 31 } 32 return ans; 33 } 34 int main() 35 { 36 long long n; 37 node t,ans; 38 t.a[0][0]=4; 39 t.a[0][1]=0; 40 t.a[1][1]=1;; 41 t.a[1][0]=2; 42 while(scanf("%lld%lld",&n,&m1)!=EOF) 43 { 44 ans=solve(t,n/2); 45 if(n%2==0) 46 cout<<(ans.a[0][0])%m1<<endl; 47 else 48 cout<<(ans.a[0][0]*2+1)%m1<<endl; 49 } 50 return 0; 51 }
快速幂的应用
如果k为偶数,那么(A+A^2+....A^K) = (A+...+A^K/2)+A^K/2*(A+...+A^K/2)
如果k为奇数,那么(A+A^2+....A^K) = (A+...+A^K/2)+A^K/2*(A+...+A^K/2)+A^k
A + A^2 + A^3 + A^4 + A^5 + A^6 =(A + A^2 + A^3) + A^3*(A + A^2 + A^3)
应用这个式子后,规模k减小了一半。我们二分求出A^3后再递归地计算A + A^2 + A^3,即可得到原问题的答案。
应用这个式子后,规模k减小了一半。我们二分求出A^3后再递归地计算A + A^2 + A^3,即可得到原问题的答案。
if(n%2==0) 先求num=A+...+A(n/2) 然后ans=num+num*A^n/2
else n=n-1 先求num=A+...+A(n/2) 然后ans=num+num*A^n/2+A^(n+1)
最易理解的代码:

1 #include<iostream> 2 #include<algorithm> 3 #include<string> 4 #include<string.h> 5 using namespace std; 6 int n,m; 7 struct node{ 8 int a[35][35]; 9 }; 10 node ONE; 11 node multi(node X,node Y)//X*Y矩阵相乘 12 { 13 node R; 14 for(int i=0;i<n;i++) 15 for(int j=0;j<n;j++) 16 { 17 R.a[i][j]=0; 18 for(int k=0;k<n;k++) 19 R.a[i][j]=(R.a[i][j]+X.a[i][k]*Y.a[k][j])%m; 20 } 21 return R; 22 } 23 node add(node X,node Y)//X+Y矩阵相加 24 { 25 node R; 26 for(int i=0;i<n;i++) 27 for(int j=0;j<n;j++) 28 { 29 R.a[i][j]=(X.a[i][j]+Y.a[i][j])%m; 30 } 31 return R; 32 } 33 node factorial(node X,int t)//X矩阵的t次方 34 { 35 node ans; 36 memset(ans.a,0,sizeof(ans.a)); 37 for(int j=0;j<n;j++)//初始化为单位矩阵 38 ans.a[j][j]=1; 39 40 while(t!=0) 41 { 42 if(t&1) 43 ans=multi(ans,X); 44 X=multi(X,X); 45 t>>=1; 46 } 47 return ans; 48 } 49 node solve(node X,int t) 50 { 51 if(t==1) 52 return X; 53 if(t%2==0) 54 { 55 node B=solve(X,t/2); 56 return multi(add(factorial(X,t/2),ONE),B);//num*(E+A^(t/2)) 57 } 58 else 59 { 60 61 node B=solve(X,t/2); 62 // 第一种 num*(E+A^(t/2))+A^t----时间复杂度高 63 node C=factorial(X,t); 64 return add(C,multi(add(factorial(X,t/2),ONE),B));//num*(E+A^(t/2))+A^t 65 // 第二种 A^((n+1)/2)+num*(E+A^((n+1)/2)) 66 // node C=factorial(X,(t+1)/2);----时间复杂度低 67 // return add(C,multi(B,add(C,ONE))); //A^((n+1)/2)+num*(E+A^((n+1)/2)) 68 69 } 70 } 71 int main() 72 { 73 node M; 74 int k; 75 scanf("%d%d%d",&n,&k,&m); 76 for(int i=0;i<n;i++) 77 for(int j=0;j<n;j++) 78 scanf("%d",&M.a[i][j]); 79 for(int i=0;i<n;i++)//单位矩阵 80 ONE.a[i][i]=1; 81 82 node ans=solve(M,k); 83 for(int i=0;i<n;i++){ 84 for(int j=0;j<n;j++) 85 { 86 if(j!=0) 87 printf(" "); 88 printf("%d",(ans.a[i][j])%m); 89 } 90 printf("\n"); 91 } 92 return 0; 93 }
总结的非常好的题集:https://www.xuebuyuan.com/3259372.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号