
判别函数Discriminant Functions
概率生成模型
- 分类的概率视角:展示具有线性决策边界的模型是如何从关于数据分布的简单假设中产生的。采用生成方法建模类条件密度\(p(\vec{x}|C_k)\)和类先验\(p(C_k)\),然后使用这些通过贝叶斯定理来计算后验概率\(p(C_k|\vec{x})\)
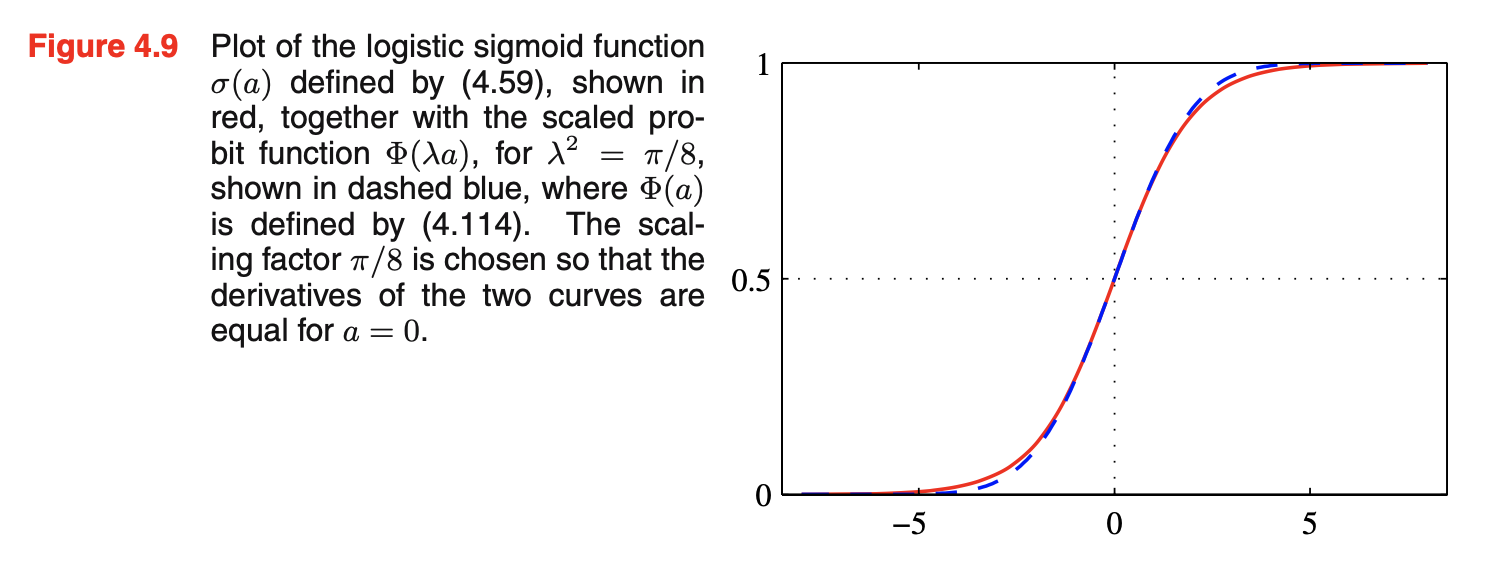
- 首先考虑两类的情况:类\(C_1\)的后验概率为\(p(C_1|\vec{x})=\frac{p(\vec{x}|C_1)p(C_1)}{p(\vec{x}|C_1)p(C_1)p(\vec{x}|C_2)p(C_2)}=\frac{1}{1+exp(-a)}=\sigma(a)\),定义\(a=ln\frac{p(\vec{x}|C_1)p(C_1)}{p(\vec{x}|C_2)p(C_2)}\)。\(\sigma(a)=\frac{1}{1+exp(-a)}\)是logistic sigmoid函数(sigmoid指S-shaped),如下图所示,其中\(\Phi(a)=\int_{-\infty}^aN(\theta|0,1)d\theta\)。logistic sigmoid函数有时也称作squashing函数,因为它将整个实轴映射到一个有限的区间。满足对称属性,\(\sigma(-a)=1-\sigma(a)\)。logistic sigmoid的逆为\(a=ln\frac{\sigma}{1-\sigma}\),称作logit函数,它表示概率比值的对数,即\(ln[p(C_1|\vec{x})/p(C_2|\vec{x})]\),也称作log odds。考虑\(a(\vec{x})\)是\(\vec{x}\)的线性函数,此时后验概率被一个一般化的线性模型控制
- 当K>2时,\(p(C_k|\vec{x})=\frac{p(\vec{x}|C_k)p(C_k)}{\sum_jp(\vec{x}|C_j)p(C_j)}=\frac{exp(a_k)}{\sum_jexp(a_j)}\),称作标准化指数normalized exponential,被当作是logistic sigmoid的多类推广。定义\(a_k=lnp(\vec{x}|C_k)p(C_k)\)。标准化指数也称作softmax函数,它表示max函数的一个平滑版本,因为对于所有\(j\ne k\),如果\(a_k>>a_j\),那么\(p(C_k|\vec{x})\simeq 1,p(C_j|\vec{x})\simeq 0\)
- 研究为类条件密度选择特定形式,首先看连续输入变量\(\vec{x}\),然后讨论离散输入
连续输入
离散特征



