ch01_Introduction
目录
例子:识别手写数字
- 每个数字对应于一张\(28 \times28\)像素的图像,可表示为一个向量\(\vec{x}\),包含784个实数
- 目标:建立一个机器,将这样的向量\(\vec{x}\)作为输入,会产生数字0-9的identity,并作为输出
- 使用手工编制的规则或启发式方法来区分数字(基于笔画的形状)
- 规则激增、规则之外的情况导致结果总是很糟糕
- 采用机器学习方法可得到更好的结果
- 训练集:有N个数字的大集合\(\{\vec{x_1},...,\vec{x_N}\}\)
- 训练集中数字的类别是已知的(通常通过单独检查和手工标记)
- 使用目标向量\(\vec{t}\)表示数字的类别,即该数字的identity。对于每个数字图像\(\vec{x}\)都有一个这样的目标向量\(\vec{t}\)
- 调整自适应模型的参数
- 运行机器学习算法的结果可表示为一个函数\(\vec{y}(\vec{x})\):以一个新的数字图像\(\vec{x}\)为输入然后产生一个输出向量\(\vec{y}\),编码方法和目标向量一样
- 函数\(\vec{y}(\vec{x})\)的精确形式在训练期间phase或学习期间被确定(基于训练数据)
- 一旦模型被训练好了,它就可以确定新数字图像(组成一个测试集)的identity
- 正确分类新例子(不同于训练所使用的例子)的能力称为泛化generalization
- 在实际应用中,输入向量的变化使得训练数据只能包含所有可能输入向量的一小部分,因此泛化是模式识别的一个中心目标
- 原始输入向量通常会被预处理,将它们转换到一个新的变量空间,使得模式识别问题更容易解决
- 数字图像通常会被平移和放缩,使得每个数字被包含在一个固定大小的box里,这大大降低了每个数字类(within each digit class)的变化
- 因为现在所有数字的位置和尺度都是一样,使得后续模式识别算法更容易区分不同的类
- 预处理阶段stage有时也被称为特征抽取,新的测试数据必须使用与训练数字相同的步骤进行预处理
- 为了加速计算,也会执行预处理。如,目标是在一个高分辨率的视频流里进行实时脸部检测,计算机每秒必须处理大量像素,而将这些直接呈现给复杂模式识别算法在计算上可能是不可行的,目标是找到可以快速计算的有用的特征,同时保留下有用的区分性信息使得能够区分faces和non-faces。然后这些特征用作模式识别算法的输入,比如矩形子区域上的图像强度intensity平均值可被有效计算evaluate。一组这样的特征被证明在快速人脸检测中非常有效。因为这样的特征数小于像素数,所以这种预处理是一种降维
- 在预处理过程中必须小心谨慎,因为信息经常被丢弃,如果这些信息对于解决问题很重要,那么系统的整体精度accuracy就会受到影响
基本概念
- 训练数据包含的例子是输入向量及其对应的目标向量,这样的应用被称作有监督学习问题
- 如上述数字识别例子,目标是将每个输入向量分配到有限数量的离散类别中的一个,称作分类问题
- 如果想要的输出由一个或更多连续变量组成,则任务被称作回归。例子:预测化学生产过程中的产量,输入包括反应物的浓度、温度和压力
- 训练数据由一组不带任何对应目标值的输入向量\(\vec{x}\)组成
- 这样的无监督学习问题的目标可以是发现数据中相似例子的groups,即聚类clustering;或去确定在输入空间中的数据分布,即密度估计;或将数据从高维空间映射到二、三维空间(为了可视化目的)
- 强化学习技术涉及在给定情况situation下寻找合适的动作以获得最大奖励reward
- 与有监督学习相比,这里的学习算法没有给出最优输出的例子,而是必须通过试错(trial and error)过程来发现它们
- 通常有一个状态和动作的序列,学习算法在其中与它的环境交互,当前动作不仅影响即时immediate奖励,还影响到所有随后时间步的奖励
- 例子:通过使用适当的强化学习技术,一个神经网络可以学习高标准地玩十五子棋backgammon游戏。这里的网络必须学会把棋盘位置作为输入,连同掷骰子的结果,并产生一个强有力的移动作为输出。这是通过让网络在一百万个游戏中与自己的副本进行对抗来实现的。一个主要的挑战是:一个十五子棋游戏可涉及几十个动作,但只有在游戏结束时,才能以胜利的形式获得奖励。因此,奖励必须适当地归因于导致它的所有移动,即使有些移动是好的,而其他不那么好。这是一个credit分配assignment问题的例子
- 强化学习的一个一般特征是在exploration(系统尝试新类型的动作来看它们有多有效)和exploitation(系统利用已知能产生高奖励的动作)之间的trade-off。过于注意exploration或exploitation都会产生不良结果
例子:多项式曲线拟合polynomial curve fitting
- 回归问题
- 假设观测到一个实值输入变量x,希望使用这个观测来预测一个实值目标变量t的值
- 综合synthetically生成数据:\(sin(2\pi x)\) with随机噪声(包含在目标值里)。输入值\(\{x_n\}\)在(0,1)内均匀生成,对应的目标值\(\{t_n\}\):先计算对应的\(sin(2\pi x)\)的值,然后加上随机噪声(标准差0.3的高斯分布)。噪声可能来自本质上intrinsically的随机过程,如放射性衰变,但更典型的是由于存在本身未被观测到的变化源variability
- 给定一个训练集:包含x的N个观测\(\mathbf{x}\equiv (x_1,...,x_N)^T\),对应t值的观测\(\mathbf{t}\equiv (t_1,...,t_N)^T\)
- 目标:利用训练集预测输入变量的某一新值\(\hat{x}\)的目标变量的值\(\hat{t}\)
- 必须从一个有限数据集中进行推广generalize;观测数据被噪声破坏,对于给定的\(\hat{x}\),\(\hat{t}\)的适当值存在不确定性uncertainty。概率论提供一个框架,以一种精确和定量的方式表达这种不确定性。决策论利用这种概率表示,根据适当的标准criteria作出最优预测
- 使用一个多项式函数来拟合数据\(y(x,\vec{w})=w_0+w_1x+w_2x^2+...+w_Mx^M=\sum_{j=0}^Mw_jx^j\),M是多项式的阶order,\(y(x,\vec{w})\)是x的非线性函数,系数\(\vec{w}\)的线性函数。函数线性于未知参数称作线性模型linear models。通过将多项式拟合到训练数据来确定系数的值:最小化一个误差error函数,衡量\(y(x,\vec{w})\)与训练数据点之间的不匹配misfit(对于任意给定\(\vec{w}\)值)。一个简单的选择是每个数据点\(x_n\)的预测\(y(x_n,\vec{w})\)和对应目标值\(t_n\)之间误差的平方的和:\(E(\vec{w})=\frac{1}{2}\sum_{n=1}^N\{y(x_n,\vec{w})-t_n\}^2\),其中\(\frac{1}{2}\)是为了后续的方便。通过选择\(\vec{w}\)的值使得\(E(\vec{w})\)尽可能小来解决曲线拟合问题。误差函数是系数\(\vec{w}\)的二次quadratic函数,它的导数(关于系数)线性于\(\vec{w}\)的元素(表示为\(\vec{w}^*\),can be found in closed form),所以误差函数的最小化有唯一解。结果多项式由\(y(x,\vec{w}^*)\)给出
- 选择多项式阶M:模型对比或模型选择model comparison or model selection的一个例子。如下图所示:M=0和M=1拟合效果差,即很差的\(sin(2\pi x)\)的表示;M=3给出\(sin(2\pi x)\)的最好拟合;M=9完全拟合训练数据,但拟合的曲线振荡厉害,导致很差的\(sin(2\pi x)\)的表示,即过拟合
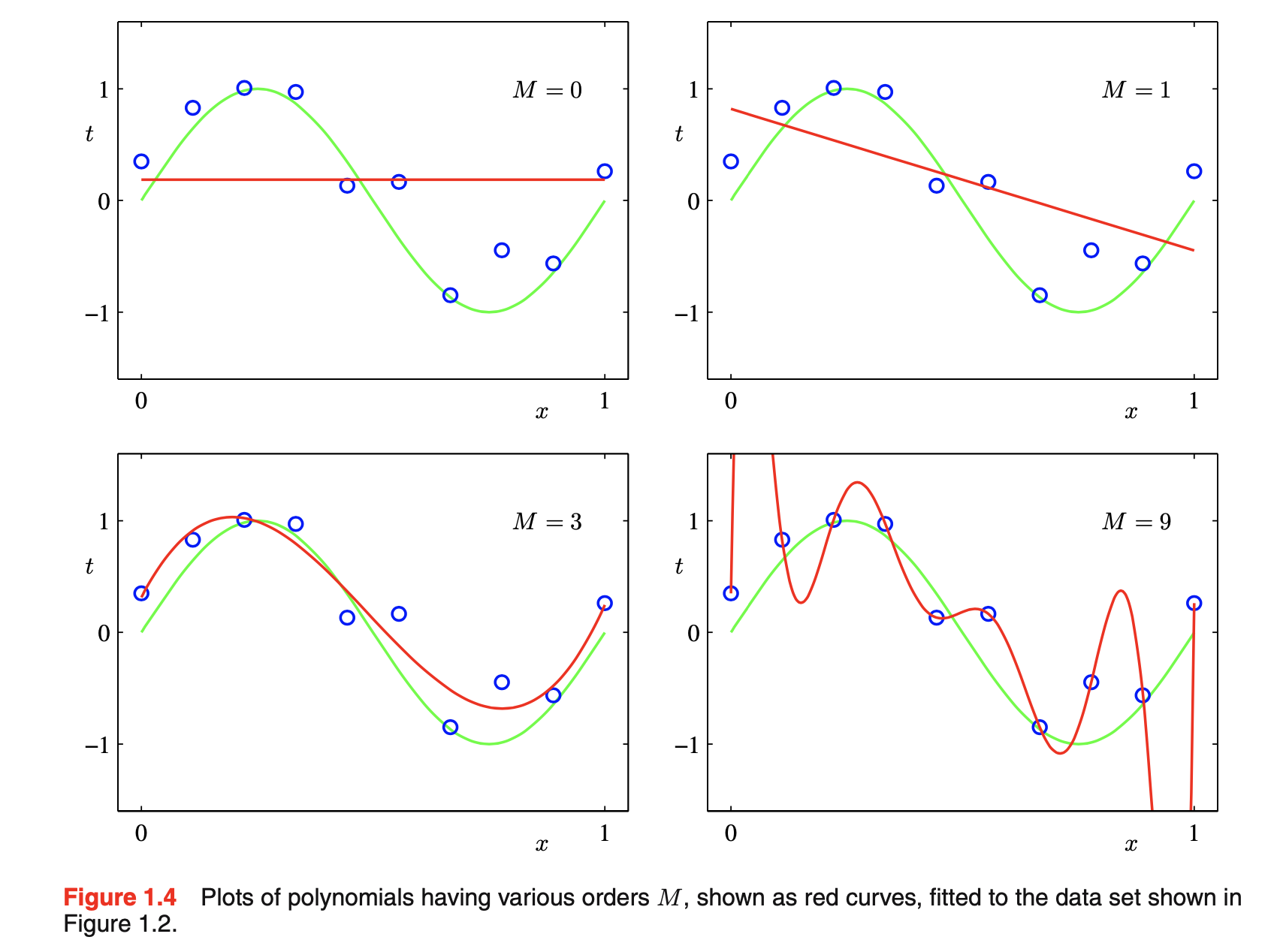
- 目标:通过对新数据作出准确的预测来达到好的泛化。通过考虑一个包含100个数据点的独立测试集,可定量地了解泛化性能对M的依赖。该测试集使用与生成训练集完全相同的程序生成,但目标值中包含的随机噪声值有新的选择。对于每个M的选择,可计算训练数据的residual value of \(E(\vec{w}^*)\),也可计算测试数据的\(E(\vec{w}^*)\)。有时使用root-mean-square(RMS)更方便:\(E_{RMS}=\sqrt{2E(\vec{w}^*)/N}\)。除以N允许我们在同等基础上on the equal footing比较不同大小的数据集;平方根确保\(E_{RMS}\)以和目标变量t相同尺度the same scale(and in the same units)被衡量。测试集的误差是衡量在给定x的新数据观测时预测t值方面我们做的有多好。如下图所示:小的M值给出相对大的测试集误差,这可归因于对应多项式相对不灵活,不能捕获\(sin(2\pi x)\)中的振荡oscillations。\(3\le M\le 8\)给出小的测试集误差,也给出合理的\(sin(2\pi x)\)的表示。M=9: 训练集误差为0(因为多项式包含10个自由度,对应于10个系数\(w_0,...,w_9\),所以可被精确调整到训练集中的10个数据点),可测试集的误差变得很大。这看起来很矛盾:因为一个给定阶的多项式包含所有低阶多项式作为特例,因此M=9多项式至少能够生成和M=3多项式一样好的结果。此外,我们可以假设新数据的最佳预测器是生成数据的函数\(sin(2\pi x)\)(事实确实如此)。我们知道\(sin(2\pi x)\)的幂级数power series expansion展开包含所有阶的项,因此我们可以预期结果会随着M的增加而单调提升。通过检查从不同阶多项式中获得的系数\(\vec{w}^*\)的值来了解这个问题。当M增大时,系数的幅度magnitude通常会变大,尤其M=9时,通过产生大的正负值,系数已根据数据进行了微调finely tune,使得对应的多项式精确匹配每个数据点。但在数据点之间(特别是在范围的末端附近near the ends of range),函数表现出大的振荡,具有更大M值的更灵活的多项式越来越适应tune目标值上的随机噪声
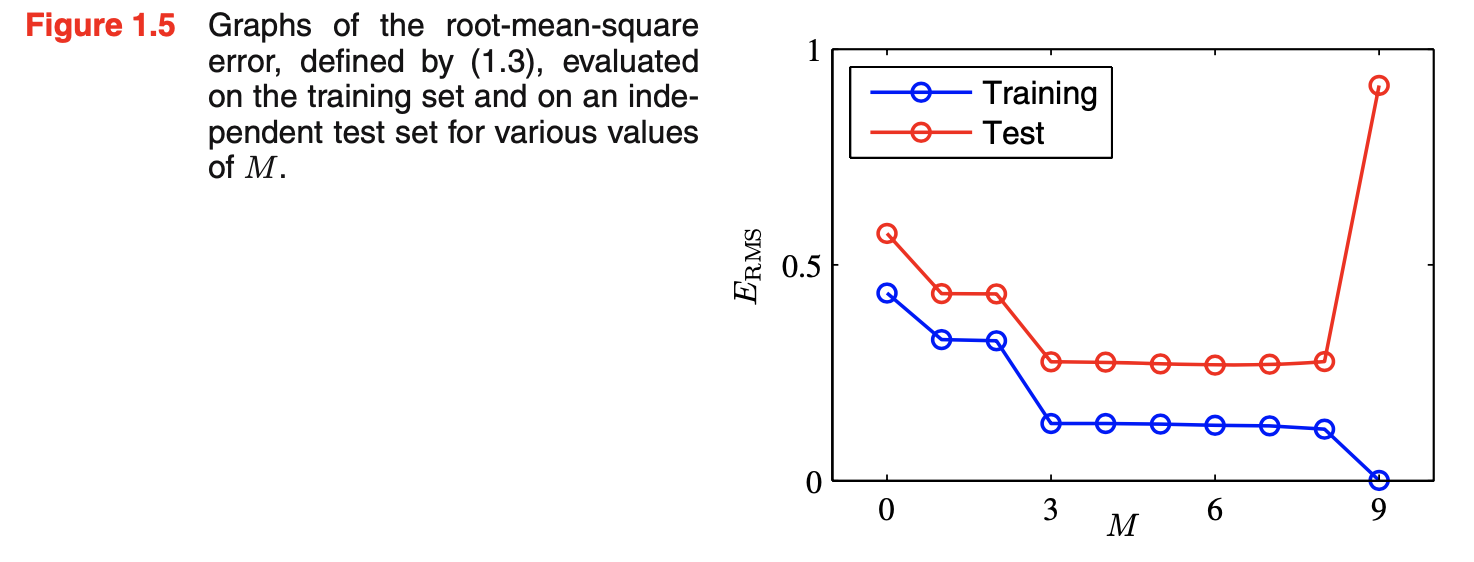
- 检查当数据集大小变化时给定模型的行为:对于一个给定模型复杂度,过拟合问题会随着数据集大小增大而变得不那么严重,也即数据集越大,我们就可以负担afford起更复杂或更灵活的模型来拟合数据。有时提倡的一种粗略的启发式方法是:数据点的数目不应少于模型中自适应参数数目的若干倍数(如5或10),但参数数量不一定是模型复杂度最适当的度量measure。另外,必须根据可用训练集的大小来限制模型中的参数数目,这是相当令人不满意。根据要解决的问题复杂度来选择模型复杂度要更合理
- 寻找模型参数的最小二乘法least squares approach代表了最大似然的一种具体情况,过拟合问题可理解为最大似然的一般属性。通过采用一种贝叶斯方法baysian approach,过拟合问题可被避免。从贝叶斯角度,使用参数数量大大超过数据点数量的模型并不困难。实际上,在贝叶斯模型中,有效参数数量会自动适应adapt数据集的大小
- 继续采用当前方法,考虑如何在实践中将其应用于可能希望使用复杂和灵活的模型的有限规模limited size的数据集。在这种情况下,控制过拟合现象的常用技术是正则化regularization,涉及在误差函数中添加一个惩罚penalty项来阻止discourage系数达到大值。最简单的惩罚项是所有系数的平方和\(\tilde{E}(\vec{w})=\frac{1}{2}\sum_{n=1}^N\{y(x_n,\vec{w})-t_n\}^2+\frac{\lambda}{2}||\vec{w}||^2,||\vec{w}||^2=\vec{w}^T\vec{w}=w_0^2+w_1^2+...+w_M^2\),系数\(\lambda\)控制govern正则化项和平方和sum-of-squares误差项的相对重要性。\(w_0\)经常会被忽略,因为包含它会导致结果依赖于目标变量的原点origin选择或者它可能被包含,但有其自身的正则化系数。上面的误差函数可被精确地最小化in closed form。这样的技术在统计学statistics literature里称为shrinkage方法methods。因为它们减小系数值。一个二次正则器regularizer的特例称为ridge regression。在神经网络里,这种方法称作weight decay。M=9及使用正则化后的误差函数:当\(ln\lambda=-18\),过拟合被抑制suppress,可得到一个更接近\(sin(2\pi x)\)的表示;当\(\lambda\)值过大,如\(ln\lambda=0\),则会得到一个差的拟合。正则化具有减小系数幅度的效果。正则化项对泛化误差的影响:训练集和测试集的RMS误差,横坐标为\(ln\lambda\)。\(\lambda\)控制模型的有效复杂度,因此决定过拟合的程度
- 如果我们试图用最小化误差函数的方法来决定实际应用,我们必须找到一种方法来确定模型复杂度的合适值。上述结果表明实现这一点的一种简单方法:获取可用数据并将其划分为用于确定系数\(\vec{w}\)的训练集和用于优化模型复杂度(M或\(\lambda\))的单独验证集seperate validation(也称hold-out set)。可是在许多情况下,这被证明太浪费有价值的训练数据,必须寻找更复杂的方法
概率论
- 例:假设有两个boxes,一红一蓝,在红盒子里有2个苹果和6个橘子,在蓝盒子里有3个苹果和1个橘子。随机选择一个盒子,并从该盒子中拿出拿出一个水果,观测到它是哪种水果后把它放回原处。重复这个过程许多次。40%时间选择红色盒子,60%时间蓝盒子。当我们从盒子里取出一个水果时,我们同样有可能选择盒子里的任何一个水果。盒子的identity是一个随机变量,表示为B,有两个可能的值r或b,水果的identity也是一个随机变量,表示为F,有两个可能值a或o
- 首先定义一个事件event发生的概率是该事件发生的次数在总试验trials次数中的分数,在试验总数达到无穷大的限度limit内。p(B)表示随机变量B上的一个分布,p(r)表示对特定值r计算的分布
- 选择红盒子的概率是4/10,蓝盒子是6/10,即p(B=r)=4/10,p(B=b)=6/10
- 两个基本概率规则:加和规则sum rule,乘积规则product rule
- 贝叶斯定理:\(p(Y|X)=\frac{p(X|Y)p(Y)}{p(X)}\),我们可以把贝叶斯定理中的分母看作是保证贝叶斯定理左边的条件概率之和在Y的所有值上等于1所需的规范化normalization常数
- 对贝叶斯定理作如下解释:如果我们在被告知所选水果的identity之前被问到选择了哪个盒子,那么我们所能得到的最完整信息是概率p(B),这称为先验概率prior,因为它是在我们观测到水果的identity之前可用的概率。一旦我们被告知水果是橘子,那么就能用贝叶斯定理来计算p(B|F),这称为后验概率posterior,因为它是在我们观测到F之后获得的概率
- 如果两个变量的联合分布分解成factorize边缘的乘积:p(X,Y)=p(X)·p(Y),那么X和Y是独立的independent。由乘积规则可得p(Y|X)=p(Y),即给定X的Y的条件分布确实与X值独立
- 除了考虑离散事件集上定义的概率外,我们还希望考虑连续变量的概率。离散变量的概率概念可推广到连续变量x上的概率密度p(x)。如果一个实值变量x的概率(落在区间\((x,x+\delta x)\))由\(p(x)\delta x \quad \text{for} \quad \delta x\to 0\)给出,那么p(x)称为x上的概率密度,即累积cumulative分布函数P(x)的导数
- x落在区间(a,b)上的概率:\(p(x\in(a,b))=\int_a^bp(x)dx\)。概率密度p(x)必须满足两个条件:\(p(x)\ge 0\quad \int_{-\infty}^{\infty}p(x)dx=1\)
- 在变量的非线性变化下,由于雅可比Jacobian因子的存在,概率密度的变换与简单函数不同。例子:考虑变量x=g(y)的一个变化,那么函数f(x)变成\(\tilde{f}(y)=f(g(y))\)。考虑概率密度\(p_x(x)\quad p_y(y)\)(后缀表明\(p_x(x)\)和\(p_y(y)\)是不同的密度),观测落在范围\((x,x+\delta x)\)(对于小的\(\delta x\)值)会被变换到范围\((y,y+\delta y)\),满足\(p_x(x)\delta x \simeq p_y(y)\delta y\),\(\simeq\)是函数之间的渐进相等。因此:\(p_y(y)=p_x(x)|\frac{dx}{dy}|=p_x(g(y))|g^{'}(y)|\)。这个属性的一个结果是:概率密度最大值的概念取决于变量的选择
- x落在区间\((-\infty,z)\)的概率由累积分布函数给出:\(P(z)=\int_{-\infty}^zp(x)dx\),\(P^{'}(x)=p(x)\)
- 有几个连续变量\(x_1,...,x_D\),由\(\vec{x}\)表示。那么可定义一个联合概率密度\(p(\vec{x})=p(x_1,...,x_D)\)。满足\(\vec{x}\)落在一个极小量infinitesimal volume\(\delta\vec{x}\)(包含点\(\vec{x}\))的概率密度由\(p(\vec{x})\delta\vec{x}\)给出。多变量multivariate概率密度必须满足:\(p(\vec{x})\ge 0,\int p(\vec{x})d\vec{x}=1\),整个\(\vec{x}\)空间的积分integral被占据take over。也可以考虑离散和连续变量组合的联合概率分布。如果x是一个离散变量,p(x)有时称作概率质量函数probability mass function,因为它可以看作是集中在concentrated at x的允许值上的一组"概率质量"probability masses。概率的加和、乘积规则以及贝叶斯定理同样可应用于概率密度或离散和连续变量的组合。例子:x和y是两个实变量,那么加和和乘积规则如下:\(p(x)=\int p(x,y)dy,p(x,y)=p(y|x)p(x)\)。将每个实变量划分成宽度为\(\Delta\)的区间,并考虑这些区间上的离散概率分布,取极限\(\Delta \to 0\),将求和转化为积分,并给出所需结果
- 涉及概率的最重要的操作之一是找到函数的加权平均值。某个函数f(x)在一个概率分布p(x)下的平均值称为f(x)的期望expectations,表示为E[f]。对于一个离散分布:\(E[f]=\sum_xp(x)f(x)\),平均值由x的不同值的相关relative概率加权。在连续变量情况下,期望用与相应概率密度的积分表示:\(E[f]=\int p(x)f(x)dx\)
- 在任一情况下,若从概率分布或概率密度中得到有限数量的N个点,那么期望可由这些点上的有限和估计:\(E[f]\simeq \frac{1}{N}\sum_{n=1}^Nf(x_n)\)。当讨论到采样方法时会广泛使用这个结果。当\(N\to \infty\),估计会变得精确
- 考虑多个变量的函数的期望:使用下标subscript来指明在哪个变量上平均。\(E_x[f(x,y)]\): 函数f(x,y)关于x的分布的平均值,是y的一个函数
- 关于一个条件分布的条件期望:\(E_x[f|y]=\sum_xp(x|y)f(x)\)
- f(x)的方差:\(var[f]=E[(f(x)-E[f(x)])^2]=E[f(x)^2]-E[f(x)]^2\),提供一个度量f(x)在其平均值附近有多大可变性variability。变量x自身的方差:\(var[x]=E[x^2]-E[x]^2\)
- 对于两个随机变量x和y,协方差为: \(cov[x,y]=E_{x,y}[\{x-E[x]\}\{y-E[y]\}]=E_{x,y}[xy]-E[x]E[y]\),表示x和y一起变化的程度。若x和y独立,则协方差消失。随机变量\(\vec{x}\)和\(\vec{y}\)是两个向量时,协方差是个矩阵:\(cov[\vec{x},\vec{y}]=E_{\vec{x},\vec{y}}[\{\vec{x}-E[\vec{x}]\}\{\vec{y}^T-E[\vec{y}^T]\}]=E_{\vec{x},\vec{y}}[\vec{x}\vec{y}^T]-E[\vec{x}][\vec{y}^T]\)。\(cov[\vec{x}]\equiv cov[\vec{x},\vec{x}]\)(向量\(\vec{x}\)各分量components之间的协方差)
- 从随机的、可重复事件的频率来观察view概率,将其称为概率的经典classical或频率者frequentist解释。转向更一般的贝叶斯视角view,概率提供不确定性的一个量化quantification
- 考虑一个不确定事件,例如月亮是否曾经在绕太阳的的轨道上运行或者北极冰盖是否会在本世纪末消失,这些事件是无法重复的,但可以考虑极地冰融化的速度有多快。若现在获得新的证据,例如从一个新的地球观测卫星收集新的诊断信息,我们可能会修正我们对冰损失率的看法。我们对这些问题的评估assessment将影响所采取的行动。例如努力减小温室气体的排放程度。在这种情况下,我们希望量化我们对不确定性的表述,并根据新的证据对不确定性进行精确的修正,以及随后能够因此采取最佳行动或作出决定。这一切都可以通过优雅的、非常普遍的general概率的贝叶斯解释来实现
- 使用概率来表示不确定性并不是一种ad-hoc选择,但如果要尊重常识common sense,同时作出理性的一致推断rational coherent inferences,这是不可避免的
- 考虑多项式曲线拟合例子:将概率的频率者概念应用于观测变量\(t_n\)的随机值似乎是合理的,但我们希望解决和量化围绕模型参数\(\vec{w}\)的适当选择的不确定性。从贝叶斯角度,可使用概率论机制machinery来描述模型参数(如\(\vec{w}\)或模型本身选择)的不确定性
- 贝叶斯定理现在有新的意义:水果identity的观测提供了相关信息,改变了所选盒子是红色的概率。贝叶斯定理通过包含进观测数据提供的证据,将先验概率转换成convert后验概率。在观测数据之前捕获关于\(\vec{w}\)的假设,即先验概率分布\(p(\vec{w})\)。观测数据\(D=\{t_1,...,t_N\}\)的影响以一个条件概率\(p(D|\vec{w})\)表示。贝叶斯定理:\(p(\vec{w}|D)=\frac{p(D|\vec{w})p(\vec{w})}{p(D)}\)。可以以后验概率\(p(\vec{w}|D)\)的形式计算\(\vec{w}\)的不确定性(在我们观测到D之后)。\(p(D|\vec{w})\)是对观测数据D计算的,可看作是参数向量\(\vec{w}\)的函数,称作似然函数likelihood,表示观测数据集在参数向量\(\vec{w}\)的不同设置下的概率。似然不是\(\vec{w}\)上的概率分布,它关于\(\vec{w}\)的积分不等于1
- 贝叶斯定理:posterior \(\propto\) likelihood \(\times\) prior。这些量都看作是\(\vec{w}\)的函数。\(p(D)\)是个规范化常数,确保后验分布是个有效的概率密度,并且积分等于1。对贝叶斯定理两边关于\(\vec{w}\)积分:\(p(D)=\int p(D|\vec{w})p(\vec{w})d\vec{w}\)
- 在频率者背景下,\(\vec{w}\)被认为是固定参数,其值由某一形式的“估计器estimator”确定。通过考虑可能的数据集D的分布,可得到该估计的误差线error bars。从贝叶斯视角来看,只有一个单独single的数据集D(实际被观测到的),参数的不确定性通过\(\vec{w}\)上的一个概率分布来表示
- 一个广泛使用的频率者估计器是最大似然maximum likelihood,\(\vec{w}\)要使得似然函数\(p(D|\vec{w})\)最大化,即选择\(\vec{w}\)的值来使得观测到的数据的概率最大化。在机器学习中,似然函数的负对数(单调递减)称作误差函数(最大化似然等价于最小化误差)。确定频率者误差线的方法是bootstrap,多个数据集被创建,假设原始数据集包含N个数据点\(\mathbf{X}=\{\vec{x_1},...,\vec{x_N}\}\),创建一个新数据集\(\mathbf{X}_B\)(随机从\(\mathbf{X}\)中得到N个点作替换,所以\(\mathbf{X}\)中有些点在\(\mathbf{X}_B\)中会重复,有些点在\(\mathbf{X}_B\)中会缺失),重复L次生成L个大小为N的数据集。通过观察不同bootstrap数据集之间的预测可变性,可以计算参数估计的统计精度
- 贝叶斯观点的一个优点是包含自然产生的先验知识。例:一枚均匀的fair-looking硬币要掷三次,每次都是正面land heads,正面概率的经典的最大似然估计会是1,表明所有未来的投掷都是正面。但有任何合理先验的贝叶斯方法会得到一个不那么极端的结果
- 关于频率论者frequentist和贝叶斯范式的相对优点merits,一直存在许多争议和争论。但事实上没有唯一unique的频率论者或甚至是贝叶斯观点。例:对贝叶斯方法的一个常见批评criticism是,先验分布的选择往往是基于数学上的便利,而不是作为任何先验信念beliefs的反映reflection。甚至通过依赖于先验选择而得到的结论的主观性也是困难的根源。减少对先验的依赖是所谓非信息so-called noninformative先验的一个动机,但这会导致比较不同模型时的困难,而且确实基于差的先验选择的贝叶斯方法很可能with high confidence得到差的结果。频率论者计算evaluation方法提供了一些避免此类问题的方法,交叉验证cross-validation等技术在模型比较等领域仍然有用
- 在很长一段时间内,贝叶斯方法的实际应用受到了严格限制,尤其是需要在整个参数空间中边际化marginalize(求和或积分)。这是进行预测或比较不同模型所必需的。采样方法的发展(如马尔可夫链蒙特卡罗)和计算机速度及内存容量的动态提升,为贝叶斯技术在一系列令人印象深刻的问题领域的实际应用打开了大门。蒙特卡罗方法非常灵活,可应用于很多模型,但它们计算量大computationally intensive,主要用于小规模问题。近来,高效的确定性近似方案deterministic approximation schemes如变分贝叶斯variational Bayes和期望传播expectation propagation被发展出来,这为采样方法提供了一种补充性complementary的替代方法,并允许贝叶斯技术在大规模应用中使用
- 连续变量的最重要的概率分布之一:正态normal或高斯Gaussian分布
- 有一个观测数据集\(\mathbf{x}=(x_1,...,x_N)^T\),假设观测从高斯分布(均值为\(\mu\),方差为\(\sigma^2\),均未知)中独立得到,想要确定来自该数据集的这些参数。数据点从同一分布独立得到称作独立同分布independent and identically distributed,缩写成i.i.d.。两个独立事件的联合概率是由每个事件的边际概率的乘积给出。给定\(\mu\)和\(\sigma^2\),数据集的概率\(p(\mathbf{x}|\mu, \sigma^2)=\prod_{n=1}^NN(x_n|\mu, \sigma^2)\),是\(\mu\)和\(\sigma^2\)的一个函数(似然函数)
- 使用一个观测数据集确定概率分布中参数的一个常见标准criterion是:找到使似然函数最大化的参数值。这似乎是一个奇怪的标准,因为最大化给定数据的参数的概率,而不是给定参数的数据的概率似乎更自然。事实上这两个标准是相关的。此时,通过最大化似然函数来确定高斯分布中未知参数\(\mu\)和\(\sigma^2\)。最大化似然函数的log更方便,大量小概率的乘积很容易降低underflow计算机的数值精确度precision,这是通过计算对数概率之和来解决的。执行一个关于\(\mu\)和\(\sigma^2\)的联合最大化,但在高斯分布情况里,\(\mu\)的解和\(\sigma^2\)的解解耦decouple,所以先计算\(\mu\)再利用该结果计算\(\sigma^2\)。最大似然方法系统systematically低估了underestimate分布的方差,这是一个称作bias现象的例子,与过拟合问题有关。最大似然解\(\mu_{ML}\)和\(\sigma_{ML}^2\)是数据集值\(x_1,...,x_N\)的函数。考虑这些量关于数据集值(它们本身来自于一个高斯分布,参数为\(\mu\)和\(\sigma^2\))的期望:\(E[\mu_{ML}]=\mu,E[\sigma_{ML}^2]=(\frac{N-1}{N})\sigma_{ML}^2\),所以on average最大似然估计会得到正确的均值,但会低估真实的方差by a factor (N − 1)/N,因为是相对于样本均值而非真实均值测量的。以下方差估计是无偏unbiased的:\(\tilde{\sigma}^2=\frac{N}{N-1}\sigma_{ML}^2=\frac{1}{N-1}\sum_{n=1}^N(x_n-\mu_{ML})^2\)。当数据点数N增加,最大似然解的偏差就不那么重要了。当\(N\to \infty\),方差的最大似然解=生成数据的分布的真实方差。事实上,除了小的N以外,这种偏差不会被证明是个严重的问题。最大似然的偏差问题根植于过拟合问题
重新来看曲线拟合
- 曲线拟合问题的目标:给定输入变量x的某个新值,基于一个包含N个输入值\(\mathbf{x}=(x_1,...,x_N)^T\)及对应目标值\(\mathbf{t}=(t_1,...,t_N)^T\)的训练数据集,能够对目标变量t作出预测。使用一个概率分布表示目标变量值上的不确定性
- 假定给定x的值,对应的t值有一个均值等于值\(y(x,\vec{w})\)的高斯分布。使用训练数据\(\{\mathbf{x}, \mathbf{t}\}\)来确定未知参数\(\vec{w}\)和\(\beta\)的值(使用最大似然)。就确定\(\vec{w}\)而言,最大化似然等价于最小化平方和误差函数sum-of-squares error function。在高斯噪声分布的假设下,平方和误差函数作为最大似然的结果出现了
- 确定好\(\vec{w}\)和\(\beta\),就可以对x的新值作出预测。因为现在有一个概率模型,所以以预测分布predictive distribution的形式来表示,即给t上的概率分布,而非简单的一个点估计point estimate
- 多项式系数\(\vec{w}\)上的先验分布:\(p(\vec{w}|\alpha)=N(\vec{w}|\vec{0}, \alpha^{-1}I)\)。根据贝叶斯定理,\(\vec{w}\)的后验分布与先验分布和似然函数的乘积成比例:\(p(\vec{w}|\mathbf{x}, \mathbf{t}, \alpha, \beta)\propto p(\mathbf{t}|\mathbf{x}, \vec{w}, \beta)p(\vec{w}|\alpha)\)。通过给定数据找到\(\vec{w}\)的最可能值来确定\(\vec{w}\),或者说最大化后验分布,称作最大后验(maximum posterior/MAP)。最大化后验等价于最小化正则化的平方和误差函数,正则化参数为\(\lambda=\alpha / \beta\)
- 尽管已经引入先验分布\(p(\vec{w}|\alpha)\),但我们仍然在做\(\vec{w}\)的点估计,所以这还不算是贝叶斯方法Bayesian treatmen。在一个完全fully贝叶斯方法里,应始终consistently应用概率的加和和乘积规则,这要求对\(\vec{w}\)的所有值积分,这样的边际化marginalizations是模式识别的贝叶斯方法的核心
- 给定训练数据\(\mathbf{x}\)和\(\mathbf{t}\),同时再给了新的测试点x,目标是去预测t值,因此希望计算预测分布\(p(t|x,\mathbf{x},\mathbf{t})\),假设参数\(\alpha\)和\(\beta\)是固定且已知的
- 贝叶斯方法就是简单对应于概率加和和乘积规则的一致consistent应用
- 预测分布:\(p(t|x,\mathbf{x},\mathbf{t})=\int p(t|x,\vec{w})p(\vec{w}|\mathbf{x},\mathbf{t})d\vec{w}\)
- 预测分布中的均值和方差依赖于x
模型选择
- 使用最小二乘法的多项式曲线拟合例子里,有一个多项式最优阶给出最优泛化。多项式的阶控制自由参数的个数,因此控制模型复杂度。正则化的最小二乘法,正则化系数\(\lambda\)也控制了模型的有效复杂度。然而,对于更复杂的模型,比如混合分布mixture distributions或神经网络,会有多个参数控制复杂度
- 除了为给定模型中的复杂度参数找到合适的值外,我们可能希望考虑一系列不同类型的模型,以便为我们的特定应用找到最好的模型
- 在最大似然方法里,由于过拟合在训练集上的性能performance不是一个好的指示器indicator(在未见unseen数据上的预测性能)。如果数据够多plentiful,一个方法是使用一些可用数据来训练一系列模型,或者给定一个有一系列复杂度参数值的模型,在独立数据independent data(有时也称作验证集validation set)上比较,选择一个有最优预测性能的。如果使用有限大小的数据集对模型设计进行多次迭代,那么可能会出现验证数据的过拟合。因此可能需要保有keep aside第三个测试集,在该测试集上最终评估所选模型的的性能
- 在许多应用中,用于训练和测试的数据有限,为了建立好模型,希望将尽可能多的可用数据用于训练。可是验证集小,则会给出预测性能相对嘈杂noisy的估计。一个解决该困境的方法是使用交叉验证cross-validation,允许可用数据的(S-1)/S被用于训练,同时使用所有数据评价assess性能。当数据尤其缺乏scarce时,可考虑S=N(总数据点数),即leave-one-out技术。交叉验证的一个主要缺点是必须执行的训练runs运行次数会增加by a factor of S,这对训练本身计算代价高昂computationally expensive的模型来说是有问题的
- 使用单独数据评价性能的交叉验证等技术的另一个问题是:对于单个模型,我们可能有多个复杂度参数(例如,可能有几个正则化参数)。在最坏的情况下,探索这些参数的设置组合可能需要进行大量的训练运行次数(随参数数量成指数增长)
- 理想情况下,一个更好的办法应该只依赖于训练数据,并且应该允许在一次训练中比较多个超参数和模型类型。因此,需要找到一个只依赖于训练数据且不会因过拟合而产生偏差suffer from bias的性能来度量measure
- 历史上各种“信息标准criteria”被提出,尝试去纠正correct最大似然的偏差(通过添加一个惩罚项来补偿compensate更复杂模型的过拟合)。如Akaike information criterion(AIC),选择该量quantity\(lnp(D|\vec{w}_{ML})-M\)最大的模型,其中\(lnp(D|\vec{w}_{ML})\)是best-fit对数似然,M是模型中可调参数数目。该量quantity的一个变体是Bayesian information criterion(BIC),但这样的标准没有考虑模型参数中的不确定性。实际上,它们倾向于选择favour过于简单overly simple的模型
维数诅咒/灾难(The Curse of Dimensionality)
- 在多项式曲线拟合例子中,只有一个输入变量x,但我们需要处理高维空间(包含许多输入变量),这带来一些严重挑战,是影响模式识别技术的一个重要因素
- 考虑一个合成数据集(oil-flow数据集),表示measurements来自一个pipeline包含油、水和气的混合。这三种物料可以在三种不同的几何configurations中的一种,即“均质homogenous”、“环状annular”和“层流laminar”,而且这三种物料materials的fractions也不同。每个数据点包含一个12维输入向量,由伽马射线密度计gamma ray densitometers测量的数据组成,该密度计测量通过管道的窄光束narrow beams的伽马射线的衰减attenuation。该数据集产生自一个旨在测量北海输油管道中石油、水和天然气比例的项目,基于双能伽马密度测量原理dual-energy gamma densitometry。想法是如果一束窄的伽马射线通过管道,光束强度的衰减提供了沿其路径的材料密度的信息,例如,油对光束的衰减比气体更强烈。单靠一次衰减测量是不够的,因为有两个自由度对应于水和油的fractions(气的fraction是多余的,因为这三个fractions必须相加得1)。为了解决这个问题,两个不同能量(即不同频率或波长)的gamma光束以相同的路径通过管道,每一个的衰减都被测量。由于不同材料的吸收absorbtion属性随能量的变化而不同,因此测量这两种能量下的衰减提供了两种信息。给定这种能量下油、水和气的吸收属性,那么计算沿伽马光束路径测量的油和水(以及天然气)的平均fractions就变得简单。但还有一个更复杂的问题,与材料沿管道的运动有关。如果flow的速度小,则油漂浮在水上,而气则浮在油上,这就是laminar或stratified flow configuration。当流速增加,更复杂的几何配置会出现。考虑两种特殊的idealizations:一是环状配置,同心圆柱体concentric cylinders(水在外围,气在中心),二是均质配置,紧密intimately混合(在湍流turbulent条件下,在高流速下发生)。single dual-energy beam给出沿路径长度测量的油和水的fractions,然而我们感兴趣于油和水的volume fractions。这可通过使用多个dual-energy gamma densitometers来解决(光束通过管道的不同区域)。有6个这样的光束,它们每一个包含a single dual-energy gamma densitometer,垂直三个,水平三个,垂直光束相对于中心轴不对称排列。因此单次观测由一个12维向量表示(包含沿每个光束路径测量的油和水的fractions),但我们感兴趣于获得管道中三相phases的整体overall volume fractions。这很像层析tomographic重建的经典问题,用于医学影像(如一个2维分布从大量1维平均值中被重建)。这里的线测量line measurements比在典型的层析成像tomography应用中要少得多。另一方面,几何配置的范围更有限,因此可从密度计数据中以合理精度预测配置和相fractions
- 为了安全起见,伽马射线的强度保持相对较弱,因此为了获得衰减的精确测量,测量的光束强度在特定时间间隔内进行积分。对于一个有限积分时间,由于伽马射线包含称为光子photons的离散能量包,因此测量的强度存在随机波动fluctuations。选择积分时间基于降低噪声级别(需要较长的积分时间)和检测流中的时间变化(需要较短的积分时间)之间的折衷compromise。
- 油流oil flow数据集是使用两种伽马能量下油、水和气吸收属性的实际已知值生成的,并选择了特定的积分时间(10s)作为典型实际设置的特征。数据集中每个点使用以下步骤独立生成:
- 1、以同等概率随机选择三相配置中的一个;
- 2、从(0,1)均匀分布中选择三个随机数\(f_1,f_2,f_3\),定义\(f_{oil}=\frac{f_1}{f_1+f_2+f_3},f_{water}=\frac{f_2}{f_1+f_2+f_3}\),在同等基础上on an equal footing对待三相并确保volume fractions相加等于1;
- 3、对6个光束线的每一个,计算有效的路径长度(通过油和水,给定相配置);
- 4、利用基于已知光束强度和积分时间的泊松分布扰动Perturb路径长度,以考虑光子统计效应the effect of photon statistics
- 数据集中的每个点包含12个路径长度测量,同时还有油和水的fractions,以及一个描述相配置的二元标签。数据集被分为训练、验证和测试集,每个包含1000个独立数据点
- 统计机器学习技术被用于从测量的12维向量预测volume fractions以及相的几何配置,这12维观测向量也被用于测试数据的可视化算法
- 这个数据集有丰富且有趣的结构:对于任意给定配置,有两个自由度对应于油和水的fractions。因此对于无限积分时间,数据将局部存在于二维流形manifold上。对于有限的积分时间,单个数据点将被光子噪声扰动离开流形。在均质相配置中,在油和水中的路径长度与油和水的fractions成线性关系,因此数据点lie close to一个线性流形。对于环状配置,相fraction和路径长度之间的关系是非线性的,因此流形也是非线性的。在分层配置下,情况更复杂。因为相fraction中小的变化会使其中一个水平相边界穿过水平光束线,,导致12维观测空间中的不连续跳跃。这样就使得分层配置的二维非线性流形分裂6个不同的segments。不同相配置的一些流形在特定点相遇,例如管道完全注满油,它对应于分层、环形和均质配置的特定实例
- 目标:使用这个数据(100个点,2个观测\(x_6,x_7\),都有标签/某个配置)作为训练集为了能够分类一个新的观测\((x_6,x_7)\),如下图所示。由于新点被大量红点包围,可假设它属于红类。但周围也有很多绿点,所以也可能属于绿类。它似乎不太可能属于蓝类。这里的直觉是:新点的身份identity应该更强烈地由训练集中的邻近点确定,而不是较远的点。事实上这种直觉被证明是合理的。如何将这个直觉变成一个学习算法:一个非常简单的方法是将输入空间划分成规则的cells,先确定测试点属于哪个cell,然后找到落在同一cell中的所有训练数据点。测试点的identity被预测为和在同一cell中有最大数目数据点的类。这种naive的方法有很多问题,但当我们考虑将其扩展到具有更多输入变量的问题时,最严重的问题之一就会变得明显,对应于更高维的输入空间。如果我们将一个空间的一个区域划分成规则的cells,那么这种cells的数目会随空间维数指数增长,指数级数量的cells的问题是:需要指数级的大量训练数据以确保cells不空,不希望在一个多变量空间中应用这种技术,需要找到一种更复杂的方法
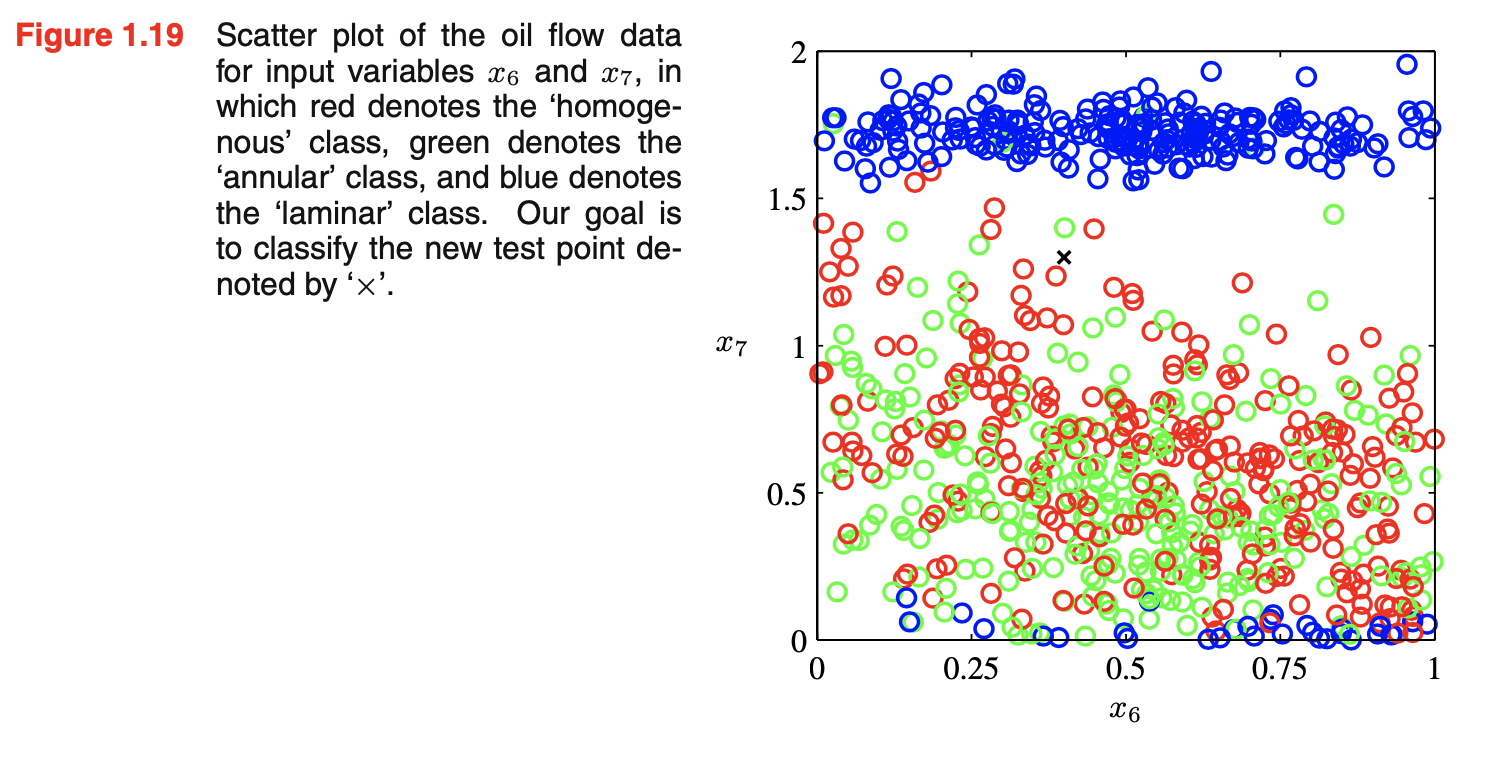
- 考虑一个合成数据集(oil-flow数据集),表示measurements来自一个pipeline包含油、水和气的混合。这三种物料可以在三种不同的几何configurations中的一种,即“均质homogenous”、“环状annular”和“层流laminar”,而且这三种物料materials的fractions也不同。每个数据点包含一个12维输入向量,由伽马射线密度计gamma ray densitometers测量的数据组成,该密度计测量通过管道的窄光束narrow beams的伽马射线的衰减attenuation。该数据集产生自一个旨在测量北海输油管道中石油、水和天然气比例的项目,基于双能伽马密度测量原理dual-energy gamma densitometry。想法是如果一束窄的伽马射线通过管道,光束强度的衰减提供了沿其路径的材料密度的信息,例如,油对光束的衰减比气体更强烈。单靠一次衰减测量是不够的,因为有两个自由度对应于水和油的fractions(气的fraction是多余的,因为这三个fractions必须相加得1)。为了解决这个问题,两个不同能量(即不同频率或波长)的gamma光束以相同的路径通过管道,每一个的衰减都被测量。由于不同材料的吸收absorbtion属性随能量的变化而不同,因此测量这两种能量下的衰减提供了两种信息。给定这种能量下油、水和气的吸收属性,那么计算沿伽马光束路径测量的油和水(以及天然气)的平均fractions就变得简单。但还有一个更复杂的问题,与材料沿管道的运动有关。如果flow的速度小,则油漂浮在水上,而气则浮在油上,这就是laminar或stratified flow configuration。当流速增加,更复杂的几何配置会出现。考虑两种特殊的idealizations:一是环状配置,同心圆柱体concentric cylinders(水在外围,气在中心),二是均质配置,紧密intimately混合(在湍流turbulent条件下,在高流速下发生)。single dual-energy beam给出沿路径长度测量的油和水的fractions,然而我们感兴趣于油和水的volume fractions。这可通过使用多个dual-energy gamma densitometers来解决(光束通过管道的不同区域)。有6个这样的光束,它们每一个包含a single dual-energy gamma densitometer,垂直三个,水平三个,垂直光束相对于中心轴不对称排列。因此单次观测由一个12维向量表示(包含沿每个光束路径测量的油和水的fractions),但我们感兴趣于获得管道中三相phases的整体overall volume fractions。这很像层析tomographic重建的经典问题,用于医学影像(如一个2维分布从大量1维平均值中被重建)。这里的线测量line measurements比在典型的层析成像tomography应用中要少得多。另一方面,几何配置的范围更有限,因此可从密度计数据中以合理精度预测配置和相fractions
- 多项式曲线拟合+高维空间:
- D维输入变量,那么一个一般的多项式(系数到3阶)为:\(y(\vec{x},\vec{w})=w_0+\sum_{i=1}^Dw_ix_i+\sum_{i=1}^D\sum_{j=1}^Dw_{ij}x_ix_j+\sum_{i=1}^D\sum_{j=1}^D\sum_{k=1}^Dw_{ijk}x_ix_jx_k\),当D增加时,独立系数的数目也增加(成比例于\(D^3\))。并非所有系数都是独立的,由于x变量中的interchange对称性。为了捕获数据中的复杂依赖,可能需要使用更高阶的多项式。对于一个M阶多项式,系数数目的增长is like\(D^M\),尽管现在这是幂律power law增长,而不是一个指数增长。但它仍指出这种方法变得笨拙unwieldy、实用性有限
- 当我们考虑更高维度空间时,通过生活在三维空间中形成的几何直觉可能会失败。如:考虑一个在D维空间中半径为1的球面sphere,问在半径\(r=1-\epsilon\)和\(r=1\)之间球的volume的分数。在D维空间中半径为r的球的volume一定scale as \(r^D\): \(V_D(r)=K_Dr^D\),上述分数表示为\(\frac{V_D(1)-V_D(1-\epsilon)}{V_D(1)}=1-(1-\epsilon)^D\)。当D越大,这个分数就倾向于1,尽管\(\epsilon\)值很小,所以在高维空间中,球的大部分volume都集中在靠近表面的薄shell
- 再考虑一个和模式识别更相关的例子:考虑高斯分布在高维空间中的行为。从笛卡尔Cartesian坐标系转换到极坐标系,然后integrate out直接directional变量,得到一个密度\(p(r)\)的表达式,作为离原点半径r的函数。\(p(r)\delta r\)是概率质量(在一个厚度为\(\delta r\)处于半径为r的薄壳里)。对于大D,高斯的概率质量集中在一个薄壳内(在某个具体的半径上)
- 在许多维度的空间中出现的严重的困难有时被称作维数的诅咒/维数灾难curse of dimensionality。并非所有在低维空间中发展的直觉都能被推广到许多维的空间。尽管维数灾难无疑会给模式识别应用带来重要问题,但它不妨碍我们找到适用于高维空间的有效技术。有两个原因:1)真实数据通常局限于confined有效维数较低的空间地区,特别是目标变量发生重要变化的方向可能或收到限制。2)真实数据通常会表现出一些平滑属性(至少是局部的),因此在大多数情况下,输入变量的微小变化将在目标变量中产生小的变化,因此我们可以利用局部interpolation-like技术来预测目标变量(对于输入变量新值)。成功模式识别技术利用这些属性中的一个或两个。例如:在制造业manufacturing中的一种应用,在传送带上捕获相同平面identical planar物体的图像,目的是确定它们的方向orientation。每个图像是高维空间(维数由像素数目确定)中的一个点。由于物体可以出现在图像的不同位置和不同方向,图像之间有三个自由度的可变性,一组图像将live on一个三维流形manifold(嵌在高维空间中)。由于物体的位置或方向与像素强度之间的复杂关系,该流形是高度非线性的。如果目标是学习一个模型,该模型可以获取输入图像并输出物体的方向,而不考虑物体的位置,那么流形中只有一个自由度的可变性是显著的
决策论Decision Theory
- 假设有一个输入向量\(\vec{x}\),同时对应目标向量\(\vec{t}\),目标是给定一个\(\vec{x}\)预测\(\vec{t}\)。对于回归问题,\(\vec{t}\)会包含连续变量,对于分类问题,\(\vec{t}\)会表示类标签。联合概率\(p(\vec{x},\vec{t})\)提供与这些变量相关的不确定性完整摘要complete summary。从一个训练集中确定\(p(\vec{x},\vec{t})\)是推断inference的一个例子。在实际应用中,必须对\(\vec{t}\)值作出具体的预测,或者更一般的说,根据我们对\(\vec{t}\)可能采取的值的理解来采取具体行动,这方面是决策论的主题。例如:医学诊断问题,得到病人的X-ray图像,确定病人是否得癌症。输入向量\(\vec{x}\)是图像中像素强度集合,输出变量t表示癌症的存在性presence,用类\(C_1\)表示,癌症的缺失absence,用类\(C_2\)表示。让t是一个二元变量,t=0对应于\(C_1\),t=1对应于\(C_2\),这样选择标签值对概率模型尤其方便
- 一般的推断问题涉及确定联合分布\(p(\vec{x},C_k)\),等价于\(p(\vec{x},t)\),给我们最完整的概率描述,尽管这是一个有用且有信息的量,但最终我们必须决定是否给病人治疗,我们希望这种选择在某种意义上是最佳的。这是决策的步骤,它是决策论的主题,告诉我们如何在适当的概率下作出最优的决策。一旦我们解决了推断问题,决策阶段通常是非常简单的,甚至是微不足道的
- 当我们得到新病人的X-ray图像\(\vec{x}\)时,目标是决定两个类中的哪一个被分配给这个图像。我们感兴趣于给定图像两个类的概率,即\(p(C_k|\vec{x})\)。使用贝叶斯定理,这些概率可表示成如下形式:\(p(C_k|\vec{x})=\frac{p(\vec{x}|C_k)p(C_k)}{p(\vec{x})}\)。在贝叶斯定理中出现的任何量都可以从联合分布\(p(\vec{x},C_k)\)中得到(关于适当的变量要么marginalizing或conditioning)。\(p(C_k)\)是先验概率,\(p(C_k|\vec{x})\)是对应的后验概率。\(p(C_1)\)表示一个人在做X-ray度量前有癌症的概率,\(p(C_1|\vec{x})\)使用贝叶斯定理修正后的对应的概率。若目标是最小化将\(\vec{x}\)分配给错误类的机会,那么会选择有更高的后验概率的类
- 最小化错误分类率misclassification rate:假设目标是尽可能减少错误分类。需要一个规则将每个\(\vec{x}\)值分配给可用类中的一个,这样的规则会将输入空间划分成区域regions\(R_k\)(称作决策区域,其中\(R_k\)中所有的点被分配给类\(C_k\),决策区域之间的界限boundaries称作决策边界decision boundaries/decision surfaces)。每个决策区域不需要连续,但会包括一些不连续的区域。为了找到最优的决策规则。一个错误发生在一个输入变量属于\(C_1\)却被分配给\(C_2\)或相反vice versa。这种情况发生的概率:\(p(mistake)=p(\vec{x}\in R_1,C_2)+p(\vec{x}\in R_2,C_1)=\int_{R_1}p(\vec{x},C_2)d\vec{x}+\int_{R_2}p(\vec{x},C_1)d\vec{x}\),前一个概率表明点来自\(C_2\),后一个概率表明点来自\(C_1\)。我们可以自由选择决策规则(将每一个点\(\vec{x}\)分配给两个类中的一个)。为了最小化\(p(mistake)\),应该使每个\(\vec{x}\)分配的类有较小的被积函数integrand值,因此若\(p(\vec{x},C_1)>p(\vec{x},C_2)\),那么应将\(\vec{x}\)分配给\(C_1\)
- \(p(\vec{x},C_k)=p(C_k|\vec{x})p(\vec{x})\),由于\(p(\vec{x})\) is common to both terms,若\(\vec{x}\)被分配给有最大后验概率的类,那么就能得到最小的出错概率
- 对于更一般的K类情况:最大化正确的概率更简单。\(p(correct)=\sum_{k=1}^Kp(\vec{x}\in R_k,C_k)=\sum_{k=1}^K\int_{R_k}p(\vec{x},C_k)d\vec{x}\)。当选择的\(R_k\)区域使得\(\vec{x}\)被分配的类的\(p(\vec{x},C_k)\)最大,即每个\(\vec{x}\)应被分配给有最大后验概率\(p(C_k|\vec{x})\)的类
- 最小化期望损失expected loss:对于许多应用,我们的目标会比简单地最小化错分数目更复杂。若病人没有癌症被错误诊断为有癌症,其后果可能是病人的痛苦以及进一步调查的需要。相反,若有癌症的病人被诊断成健康,结果会是因缺乏治疗而过早死亡。因此这种类型错误的结果会很不同。尽量减少第二类错误,尽管需要以增加第一类错误为代价
- 引入损失loss函数或称为成本cost函数,该函数是对在作出任何可用的决策或行动时所产生的损失的单一、全面的衡量。我们的目标是最小化损失,或最大化效用utility函数
- 假设对于\(\vec{x}\)的一个新值,真类是\(C_k\),将\(\vec{x}\)分配给\(C_j\)(\(j\)可能等于也可能不等于k)。用\(L_{kj}\)表示损失,可看作是损失矩阵(作出正确决策时无损失,健康病人被诊断出有癌症损失为1,有癌症病人被诊断为健康损失为1000)。损失函数依赖未知的真类,对于给定输入变量\(\vec{x}\),真类中的不确定性通过联合概率\(p(\vec{x},C_k)\)来表示
- 最小化平均损失:\(E[L]=\sum_k\sum_j\int_{R_j}L_{kj}p(\vec{x},C_k)d\vec{x}\)。目标是选择\(R_j\)来最小化期望损失。对于每一个\(\vec{x}\),应该最小化\(\sum_kL_{kj}p(\vec{x},C_k)\)。根据\(p(\vec{x},C_k)=p(C_k|\vec{x})p(\vec{x})\)来消除common factor of\(p(\vec{x})\)。因此最小化期望损失的决策规则:将每一个新\(\vec{x}\)分配给类j(\(\sum_kL_{kj}p(C_k|\vec{x})\)量最小)
- 拒绝选择reject option:分类误差来自于后验概率\(p(C_k|\vec{x})\)的最大值显著小于unity(等价于联合分布\(p(\vec{x},C_k)\)有comparable的值)的输入空间的区域。这些区域里我们对class membership相对不确定。在一些应用中,避免在困难的情况下作出决策是适当的,因为预期对那些作出分类决策的例子的误差率较低。这称作拒绝选择reject option。如:使用一个自动系统来对那些毫无疑问属于正确类别的X-ray图像进行分类,同时让人类专家对那些更模糊的情况进行分类,这可能是适当的
- 如下图所示,引入一个阈值\(\theta\),拒绝那些输入\(\vec{x}\)(其最大后验概率\(p(C_k|\vec{x}) \le \theta\))(\(\theta=1\):所有例子都被拒绝;有K类,\(\theta<\frac{1}{K}\):没有例子会被拒绝)。在给定损失矩阵的情况下,可以很容易扩展拒绝标准,使期望损失最小,同时考虑拒绝决策时所产生的损失
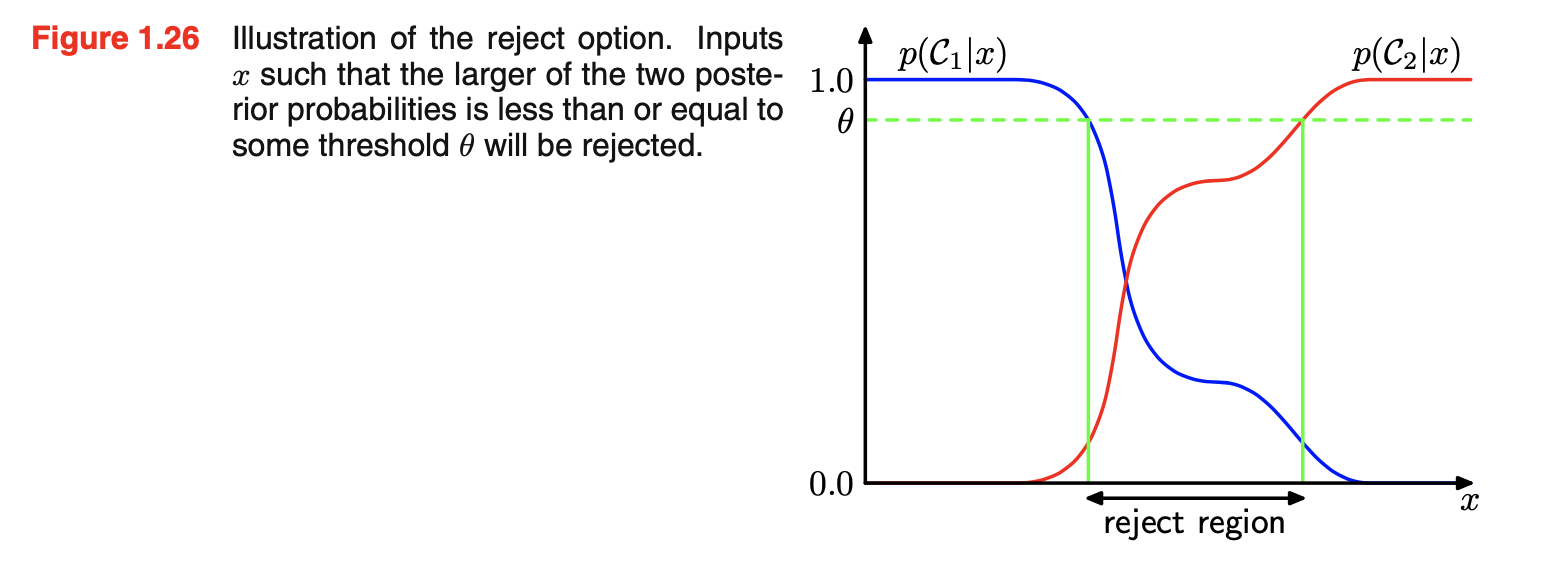
- 如下图所示,引入一个阈值\(\theta\),拒绝那些输入\(\vec{x}\)(其最大后验概率\(p(C_k|\vec{x}) \le \theta\))(\(\theta=1\):所有例子都被拒绝;有K类,\(\theta<\frac{1}{K}\):没有例子会被拒绝)。在给定损失矩阵的情况下,可以很容易扩展拒绝标准,使期望损失最小,同时考虑拒绝决策时所产生的损失
- 推断和决策
- 将分类问题分成两个独立的阶段separate stages:
- 1、推断阶段:使用训练数据学习\(p(C_k|\vec{x})\)的模型
- 2、决策阶段:使用这些后验概率来作出最优类分配
- 另一种可能性是同时解决这两个问题:简单地学习一个函数,将输入\(\vec{x}\)直接映射到决策,这样的函数称作判别函数discriminant function
- 三种不同的方法解决决策问题(按复杂度递减的顺序排列)
- a. 先解决推断问题(单独地为每个类\(C_k\)确定class-conditional密度\(p(\vec{x}|C_k)\)),同时单独地推断先验类概率\(p(C_k)\)。使用贝叶斯定理:\(p(C_k|\vec{x})=\frac{p(\vec{x}|C_k)p(C_k)}{p(\vec{x})}\)找到后验类概率\(p(C_k|\vec{x})\)。贝叶斯定理中的分母可用分子中出现的量来表示:\(p(\vec{x})=\sum_kp(\vec{x}|C_k)p(C_k)\)。等价地,可直接建模联合分布\(p(\vec{x},C_k)\),然后标准化得到后验概率,找到后验概率后,使用决策论来确定每个新输入\(\vec{x}\)的class membership。显式或隐式建模输入和输出分布的方法称作生成模型generative models,因为从它们中采样可能生成输入空间的合成数据
- b. 先解决推断问题(确定后验类概率$$p(C_k|\vec{x})),然后使用决策论来为每个新\(\vec{x}\)分配类。直接建模后验概率的方法称作判别模型discriminative models
- c. 找到一个函数\(f(\vec{x})\),称作判别函数,将每个输入\(\vec{x}\)直接映射到一个类标签。如在两类问题中,\(f(·)\)是一个二元值,\(f=0\)代表\(C_1\),\(f=1\)代表\(C_2\)。在这种情况下,概率没起作用
- 以上三种选择的相对优点relative merits
- a是最苛刻的demanding,因为它涉及找到\(\vec{x}\)和\(C_k\)的联合分布。对于许多应用,\(\vec{x}\)会有高维度,结果我们需要一个大的训练集来确定class-conditional密度达到合理的精度。类先验\(p(C_k)\)可被估计(训练集中每类数据点的分数)。该方法的一个优点是允许数据\(p(\vec{x})\)的边缘密度从\(p(\vec{x})=\sum_kp(\vec{x}|C_k)p(C_k)\)中确定。这对于检测在模型下有低概率且预测精度较低的新数据点是有用的,称作异常检测outlier detection或新奇检测novelty detection。可若我们我们只希望做分类决策,那么找联合分布p(\vec{x},C_k)会浪费计算资源且特别需求数据(实际上只需要后验概率\(p(C_k|\vec{x})\),可通过方法b直接获得)。实际上,class-conditional密度会包含很多对后验概率没什么影响的结构。更简单的方法是c,使用训练数据找到一个判别函数\(f(\vec{x})\),就\(\vec{x}\)直接映射到一个类标签,因此将推断和决策阶段结合成一个单独的学习问题。但c无法得到后验概率\(p(C_k|\vec{x})\)。有许多强有力的理由要计算后验概率:
- 最小化风险risk:考虑一个问题,其中损失矩阵中的元素需要不时地修改(比如会在金融应用中发生)。如果知道了后验概率,我们可以简单修改最小风险决策标准(通过适当修改\(\sum_kL_{kj}p(C_k|\vec{x})\))。如果我们只有一个判别函数,那么损失矩阵的任何改变都需要返回到训练数据,重新解决分类问题
- 拒绝选项:后验概率允许我们确定一个拒绝标准(给定一个拒绝数据点比例,最小化错分类率或更一般期望损失)
- 补偿类先验:假设已经收集了大量X-ray图像作为训练数据(为了建立一个自动筛选screening系统)。因为癌症是稀少的(每1000个例子中只有一个例子是有癌症的),若使用这样一个数据集来训练一个可调模型,会碰到严重的困难,由于癌症类的小比例,例如,将所有点都分配给正常类的分类器会达到99.9%的精度。很难避免这种trival的解法。甚至大数据集也只包含很少的X-ray图像与癌症相关的例子,所以学习算法不会暴露在这类图像的大量例子中,因此不太可能很好推广。平衡的数据集(每个类有相同的数目的的例子)能找到一个更精确的模型,然而,我们必须补偿我们对训练数据修改的影响。假设已经用了这样一个修改后的数据集,且发现了后验概率的模型。从贝叶斯定理可看到后验概率与先验概率(每个类点的比例)成比例。因此我们可简单地从我们人工平衡的数据集中获得后验概率,首先除以数据集中的类分数,然后乘以人群(我们需要应用模型的人群)中的类分数
- 结合模型Combining models:对于复杂应用,会希望将问题分解成若干个更小的子问题,每个子问题可被一个单独的模块处理。例如:可从血液测试和X-ray图像中获得信息。不是将所有这些异质信息组合进一个大的输入空间,而是去建立一个系统来解释X-ray图像、另一个不同的系统来解释血液数据会更有效。只要这两个模型中的每一个给出类的后验概率,我们就可以系统组合输出(使用概率规则)。这么做的一个简单方法是:对于每个类,X-ray图像的输入分布,用\(\vec{x}_I\)表示,和血液数据的输入分布,用\(\vec{x}_B\)表示,是独立的: \(p(\vec{x}_I,\vec{x}_B|C_k)=p(\vec{x}_I|C_k)p(\vec{x}_B|C_k)\),这是条件独立conditional independence属性的一个例子,条件独立假设是朴素贝叶斯naive Bayes模型的一个例子。给定X-ray和血液数据,后验概率则为:\(p(C_k|\vec{x}_I,\vec{x}_B)\propto p(\vec{x}_I,\vec{x}_B|C_k)p(C_k)\propto p(\vec{x}_I|C_k)p(\vec{x}_B|C_k)p(C_k)\propto \frac{p(C_k|\vec{x}_I)p(C_k|\vec{x}_B)}{p(C_k)}\)。因此需要类先验\(p(C_k)\),能很容易从每个类的数据点比例估计,然而需要标准化结果后验概率,使它们相加等于1。联合边缘分布\(p(\vec{x}_I,\vec{x}_B)\)通常不会在朴素贝叶斯模型下分解factorize
- a是最苛刻的demanding,因为它涉及找到\(\vec{x}\)和\(C_k\)的联合分布。对于许多应用,\(\vec{x}\)会有高维度,结果我们需要一个大的训练集来确定class-conditional密度达到合理的精度。类先验\(p(C_k)\)可被估计(训练集中每类数据点的分数)。该方法的一个优点是允许数据\(p(\vec{x})\)的边缘密度从\(p(\vec{x})=\sum_kp(\vec{x}|C_k)p(C_k)\)中确定。这对于检测在模型下有低概率且预测精度较低的新数据点是有用的,称作异常检测outlier detection或新奇检测novelty detection。可若我们我们只希望做分类决策,那么找联合分布p(\vec{x},C_k)会浪费计算资源且特别需求数据(实际上只需要后验概率\(p(C_k|\vec{x})\),可通过方法b直接获得)。实际上,class-conditional密度会包含很多对后验概率没什么影响的结构。更简单的方法是c,使用训练数据找到一个判别函数\(f(\vec{x})\),就\(\vec{x}\)直接映射到一个类标签,因此将推断和决策阶段结合成一个单独的学习问题。但c无法得到后验概率\(p(C_k|\vec{x})\)。有许多强有力的理由要计算后验概率:
- 将分类问题分成两个独立的阶段separate stages:
- 回归的损失函数:
- 曲线拟合的决策阶段:为每个输入\(\vec{x}\)的t值选择一个特定的估计\(y(\vec{x})\),即选择\(y(\vec{x})\)来最小化\(E[L]\),这里的\(E[L]=\int\int\{y(\vec{x})-t\}^2p(\vec{x},t)d\vec{x}dt\)
- 已知最优解是条件期望\(E_t[t|\vec{x}]\),则\(E[L]=\int\{y(\vec{x})-E[t|\vec{x}]\}^2p(\vec{x})d\vec{x}+\int\{E[t|\vec{x}]-t\}^2p(\vec{x})d\vec{x}\)
- 要确定的\(y(\vec{x})\)只在第一项。当\(y(\vec{x})=E[t|\vec{x}]\)时最小化。此时该项消失。最后一项是t分布的方差,averaged over \(\vec{x}\),表示目标数据内在的变异性,可当作是噪声。由于它独立于\(y(\vec{x})\),所以它表示损失函数的不可约irreducible最小值
- 和分类问题一样,我们也可以确定适当的概率,然后用它们做最优决策,或建立模型来直接做决策。有三种不同的方法来解决回归问题(按复杂度递减的顺序排列):
- a. 先解决推断问题(确定联合密度\(p(\vec{x},t)\)),然后标准化找到条件密度\(p(t|\vec{x})\),最后边际化来找到条件平均: \(\int tp(t|\vec{x})dt=E_t[t|\vec{x}]\)
- b. 先解决推断问题(确定条件密度\(p(t|\vec{x})\)),然后边际化找到条件平均
- c. 直接从训练数据中找到一个回归函数\(y(\vec{x})\)
- 以上三种方法的相对优点和分类问题一样
- 平方损失不是回归损失函数的唯一选择。实际上,平方损失存在导致更差结果的情况,此时需要开发更复杂的方法。当条件分布\(p(t|\vec{x})\)是multimodal(经常会出现在逆问题的解中),考虑平方损失的一个简单推广,称作Minkowski loss,期望是\(E[L_q]=\int\int |y(\vec{x})-t|^qp(\vec{x},t)d\vec{x}dt\),当q=2时就是期望平均损失。\(E[L_q]\)的最小值:当q=2时由条件平均值conditional mean给出,当q=1时由条件中位数conditional median给出,当\(q\to 0\)时,由条件众数conditional mode给出
信息论Information Theory
- 考虑一个离散随机变量x,当我们观测到这个变量的一个具体值时能得到多少信息。信息量amount可当作是学习到x值的"惊讶程度degree of surprise"。当被告知一个高度不可能事件发生了,比起被告知一件很可能的事件发生,我们能得到更多信息。当这个事件一定会发生,则得不到信息。对信息内容的度量因此取决于概率分布\(p(x)\),因此我们寻找一个量\(h(x)\),即信息的定义,它是\(p(x)\)的单调函数,表达信息内容。\(h(·)\)的形式可找到:有两个事件x和y,不关联unrelated,那么从观测这两个事件获得的信息应该是分别从它们中获得的信息总和,即\(h(x,y)=h(x)+h(y)\)。两个不相关事件是统计上独立的,即\(p(x,y)=p(x)p(y)\)。\(h(x)\)一定由\(p(x)\)的对数给出,即\(h(x)=-log_2(p(x))\),负数确保信息是\(\ge 0\)。低概率事件x对应于高信息内容。对数基的选择是任意的,采用信息论中流行的以2为基数的对数的惯例。在这种情况下,\(h(x)\)的units是"bits"/binary digits
- 现有一个发送者想要传输以一个随机变量的值给一个接收者,在传输过程中的信息平均量由\(h(x)=-log_2p(x)\)关于\(p(x)\)的期望获得:\(H[x]=-\sum_xp(x)log_2p(x)\),这个重要量称作随机变量x的熵entropy。已知\(lim_{p\to 0}plog_2p=0\),可得到\(p(x)log_2p(x)=0\)
- 考虑一个随机变量x有8个可能状态,每一个都有同样的可能性equally likely。为了把x的值给一个接收者,需要传输一条长度为3bits的信息。这个变量的熵:\(H[x]=-8\times \frac{1}{8}log_2\frac{1}{8}=3bits\)。考虑一个变量有8个可能的状态{a, b, c, d, e, f, g, h},对应概率为\({\frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{16},\frac{1}{64},\frac{1}{64},\frac{1}{64},\frac{1}{64}}\),此时的熵为\(H[x]=-\frac{1}{2}log_2\frac{1}{2}-\frac{1}{4}log_2\frac{1}{4}-\frac{1}{8}log_2\frac{1}{8}-\frac{1}{16}log_2\frac{1}{16}-\frac{4}{64}log_2\frac{1}{64}=2bits\)。比起均匀分布,非均匀nonuniform分布有更小的熵
- 考虑如何传输变量状态的identity给一个接收者。我们可以像之前一样使用3bits的数字。但我们可以利用非均匀分布(使用更短的码codes来表示更可能的事件probable events,更长的码来表示更不可能的事件,希望得到一个更短的平均码长度)。例如,使用以下code strings集合0, 10, 110, 1110, 111100, 111101, 111110, 111111来表示状态{a, b, c, d, e, f, g, h},要传输的平均码长度为:\(\frac{1}{2}\times 1+\frac{1}{4}\times 2+\frac{1}{8}\times 3+\frac{1}{16}\times 4+4\times \frac{1}{64}\times 6=2bits\),和随机变量的熵值一样。不能使用更短的code strings,因为必须能够消除歧义disambiguate a concatenation of such strings into its component parts,例如,11001110唯一解码到状态序列c a d
- 熵和最短编码长度之间的关系是一种普遍的关系。无噪编码定理noiseless coding theorem:熵是一个下界(传输随机变量状态序列所需的bits数目)
- 从现在起,要使用自然对数natural logarithm定义熵。此时,熵是以"nats"为单位而非"bits"来度量,只差一个因子ln2
- 以信息平均量(需要指明随机变量的状态)的形式介绍熵
- 事实上,熵的概念起源于物理学,它是在平衡热力学equilibrium thermodynamics的背景下引入的。后来随着统计力学statistical mechanics的发展,熵作为一种无序disorder的度量得到了更深入的解释
- 考虑一组N个相同对象,这些对象被划分到一组容器中bins,满足第i个bin中有\(n_i\)个对象。考虑将对象分配到bins的不同方法的数目。有N个方法选择第一个对象,(N-1)个方法选择第二个,...导致有N!个方法去将所有N个对象分配到bins,但我们不想区分每个bin中的对象的rearrangements,在第i个bin中有\(n_i!\)个方法reorder对象。所有将N个对象分配到bins中共有的方法数:\(W=\frac{N!}{\prod_in_i!}\)称作multiplicity,然后熵被定义为multiplicity的对数,被一个适当的常数放缩:\(H=\frac{1}{N}lnW=\frac{1}{N}lnN!-\frac{1}{N}\sum_ilnn_i!\)。应用Stirling’s approximation(\(lnN!=NlnN-N\))和\(\sum_in_i=N\),得到\(H=-lim_{N\to \infty}\sum_i(\frac{n_i}{N})ln(\frac{n_i}{N})=-\sum_ip_ilnp_i\),\(p_i=lim_{N\to \infty}(\frac{n_i}{N})\):一个对象被分配给第i个bin的概率。用物理术语,bins中对象的具体arrangements称作microstate,occupation numbers的整体分布由\(\frac{n_i}{N}\)表示,称作macrostate。multiplicity W也称作macrostate的权重
- 将bins解释成离散随机变量X的状态\(x_i\),\(p(X=x_i)=p_i\),则随机变量X的熵为\(H[p]=-\sum_ip(x_1)lnp(x_i)\)。在几个值上具有尖锐峰的离散分布\(p(x_i)\)会有一个相对低的熵,那些更均匀地分布在许多值上会有更高的熵,如下图所示。因为\(0\le p_i \le 1\),所以熵是非负的。当某个\(p_i=1\),其余\(p_{j\ne i}=0\)时取到最小值0。最大熵的配置:使用一个拉格朗日乘子Lagrange multiplier最大化H来对概率施加标准化约束。所有的\(p(x_i)\)都相等且\(p(x_i)=\frac{1}{M}\)(M是状态\(x_i\)的总数),对应的熵值是H=lnM
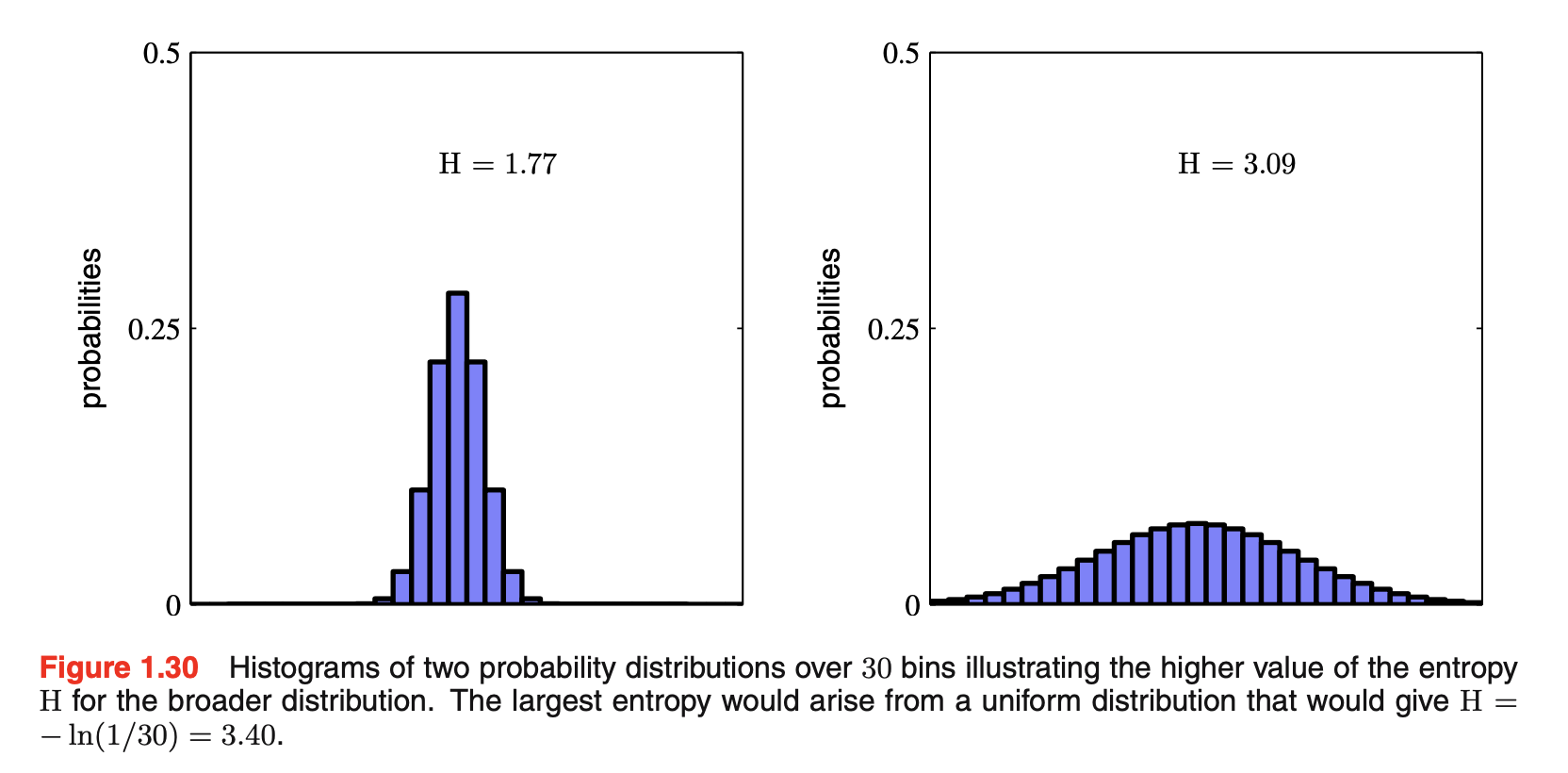
- 延展熵的定义来包括连续变量x上的分布\(p(x)\)。先将x划分成宽度为\(\Delta\)的bins,然后假设\(p(x)\)是连续的,根据平均值理论mean value theorem,对于每一个bin,一定存在这样的\(x_i\)满足:\(\int_{i\Delta}^{(i+1)\Delta}p(x)dx=p(x_i)\Delta\)。可通过当x落在第i个bin中时,将任何x值赋予\(x_i\)来离散化quantize连续变量x,然后观测到\(x_i\)的概率就为\(p(x_i)\Delta\),这给出了一个离散分布。熵的形式如下:\(H_{\Delta}=-\sum_ip(x_i)\Delta ln(p(x_i)\Delta)=\sum_ip(x_i)\Delta lnp(x_i)-ln\Delta\),又\(\sum_ip(x_i)\Delta=1\),忽略第二项的\(-ln\Delta\),考虑\(lim\Delta \to 0\),第一项会接近approach\(p(x)lnp(x)\)的积分,\(lim_{\Delta \to 0}\{\sum_ip(x_i)\Delta lnp(x_i)\}=-\int p(x)lnp(x)dx\),等式右侧称作微分熵differential entropy。熵的离散和连续形式区别在一个量\(ln\Delta\),当\(lim\Delta\to 0\)时发散diverge。这反映了精确地指定连续变量需要大量的位bits。对于定义在多个连续变量上的密度,由\(\vec{x}\)表示。微分熵如下:\(H[\vec{x}]=-\int p(\vec{x})lnp(\vec{x})d\vec{x}\)。在离散分布情况下,最大熵配置对应于一个概率的均匀分布
- 现在考虑一个连续变量的最大熵配置。为了很好定义这个最大值,有必要约束\(p(x)\)的第一阶和第二阶矩moments,同时保留标准化约束。因此最大化微分熵时有三个约束:1)\(\int_{\infty}^{\infty}p(x)dx=1\);2)\(\int_{\infty}^{\infty}xp(x)dx=\mu\);3)\(\int_{\infty}^{\infty}(x-\mu)^2p(x)dx=\sigma^2\)。使用拉格朗日乘子来执行被约束的最大化。最后的结果\(p(x)=\frac{1}{(2\pi \sigma^2)^{1/2}}exp\{-\frac{(x-\mu)^2}{2\sigma^2}\}\),所以最大化微分熵的分布是高斯。当我们最大化熵时没有约束分布是非负的,可因为结果确实是非负的,所以这样的约束没有必要。计算高斯的微分熵:\(H[x]=\frac{1}{2}\{1+ln(2\pi \sigma^2)\}\),因此我们再次看到由于分布变得更广而熵增(即当\(\sigma^2\)增加)。这个结果也显示了微分熵不同于离散熵,在于前者可为负(因为\(H[x]<0\)当\(\sigma^2<1/(2\pi e)\))
- 假设有一个联合分布\(p(\vec{x},\vec{y})\),我们从该分布中得到\(\vec{x}\)和\(\vec{y}\)的成对值,若\(\vec{x}\)的一个值已知,那么用于指定\(\vec{y}\)值的额外信息是\(-lnp(\vec{y}|\vec{x})\),因此用于指定\(\vec{y}\)的平均额外信息为:\(H[\vec{y}|\vec{x}]=-\int\int p(\vec{y},\vec{x})lnp(\vec{y}|\vec{x})d\vec{y}d\vec{x}\),称作给定\(\vec{x}\)的\(\vec{y}\)的条件熵。使用乘积规则,条件熵满足以下关系:\(H[\vec{x},\vec{y}]=H[\vec{y}|\vec{x}]+H[\vec{x}]\),等式左边为\(p(\vec{x},\vec{y})\)的微分熵,右边第二项为边际分布\(p(\vec{x})\)的微分熵。因此描述\(\vec{x}\)和\(\vec{y}\)所需的信息由单独描述\(\vec{x}\)所需的信息加上给定\(\vec{x}\)来描述\(\vec{y}\)所需的额外信息的总和给出
- 相关熵和互信息Relative entropy and mutual information
- 将信息论中的概念与模式识别联系起来
- 考虑某个未知分布\(p(\vec{x})\),假设已经用一个近似分布\(q(\vec{x})\)来建模它。使用\(q(\vec{x})\)来创建一个coding scheme(将\(\vec{x}\)值传输给一个接收者)。指定\(\vec{x}\)值所需的平均额外信息量(in nats)(假设选择一个有效的coding scheme)(使用\(q(\vec{x})\)而非真是分布\(p(\vec{x})\)):\(KL(p||q)=-\int p(\vec{x})lnq(\vec{x})d\vec{x}-(-\int p(\vec{x})lnp(\vec{x})d\vec{x})=-\int p(\vec{x})ln\{\frac{q(\vec{x})}{p(\vec{x})}\}d\vec{x}\),称作分布\(p(\vec{x})\)和\(q(\vec{x})\)之间的相关熵或Kullback-Leibler divergence散度或KL散度。这不是一个对称量:\(KL(p||q)\ne KL(q||p)\)。KL散度满足\(KL(p||q)\ge 0\),等号当且仅当\(p(\vec{x})=q(\vec{x})\)取到
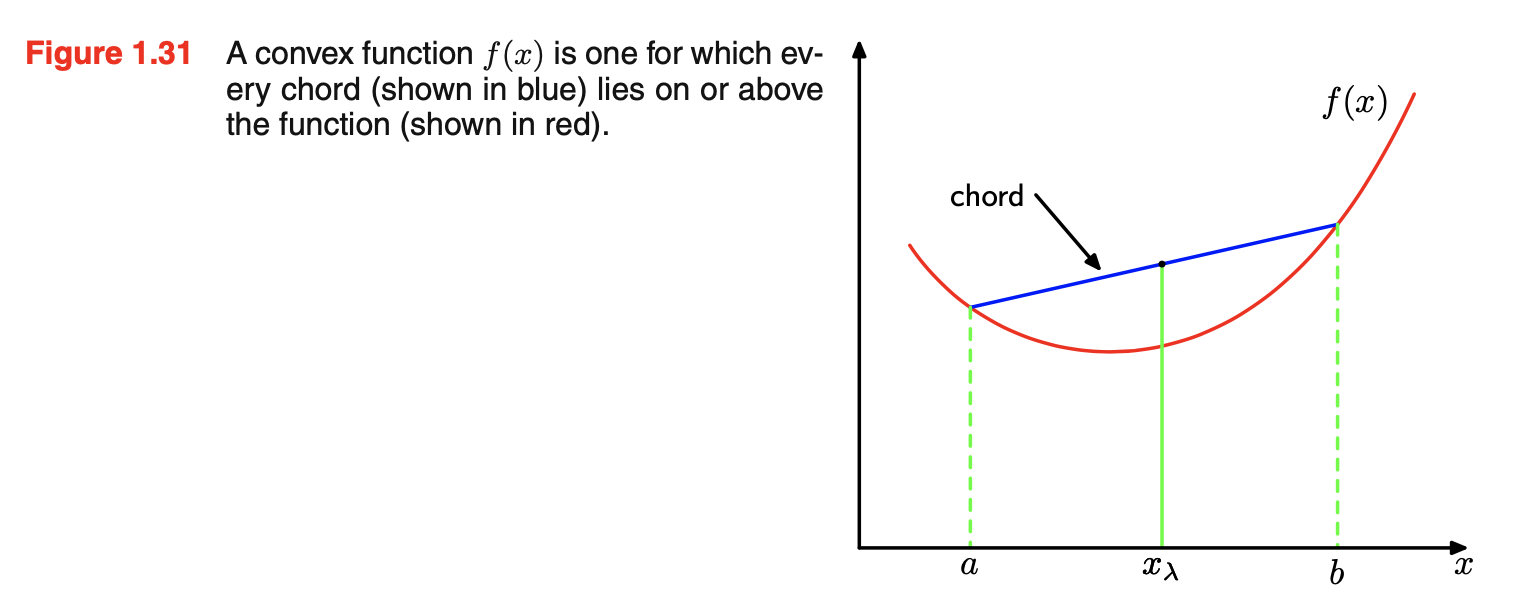
- 引入凸convex函数的概念:一个函数f(x)如果具有每个chord(函数上两点之间的连线)都on or above函数,则这个函数是凸的,如下图所示。x的任何值(在区间从x=a到x=b)可写成\(\lambda a+(1-\lambda)b(0\le \lambda\le 1)\)。在chord上的点是\(\lambda f(a)+(1-\lambda)f(b)\),函数的对应值为\(f(\lambda a+(1-\lambda)b)\)。Convexity表明:\(f(\lambda a+(1-\lambda)b) \le \lambda f(a)+(1-\lambda)f(b)\),等价于要求函数的二阶导数处处为正。凸函数的例子:\(xlnx(x>0)\)、\(x^2\)。如果等号只在\(\lambda=0\)或\(\lambda=1\)时满足,则该函数称作严格凸strictly convex。如果一个函数有相反的属性,即每个chord都on or below函数,则称作凹的concave,同时也有严格凹的定义。若一个函数f(x)是凸的,则-f(x)是凹的
- 可将KL散度解释成两个分布\(p(\vec{x})\)和\(q(\vec{x})\)的不相似性dissimilarity的度量
- 数据压缩data compression和密度估计density estimation(建模一个未知分布的问题)有一个紧密intimate的关系,因为当我们知道真实分布时最有效的压缩达成了。若使用一个不同于真实分布的分布,则必须有一个效率较低less efficient的编码,并且平均来讲,必须传输的额外信息(至少)等于两个分布之间的KL散度。假设数据从一个未知分布\(p(\vec{x})\)(我们想要建模)被生成,使用某个参数parametric分布\(q(\vec{x}|\vec{\theta})\)估计这个分布,由一组可调参数\(\vec{\theta}\)控制,如一个多变量multivariate高斯。一个确定\(\vec{\theta}\)的方法是关于\(\vec{\theta}\)最小化\(p(\vec{x})\)和\(q(\vec{x}|\vec{\theta})\)之间的KL散度。我们不能直接这么做,因为\(p(\vec{x})\)未知。但假设我们已经观测到一个训练点\(\vec{x}_n\)(从\(p(\vec{x})\)中)的有限集合,n=1,...,N。那么关于\(p(\vec{x})\)的期望可用一个这些点上的有限和来估计:\(KL(p||q)\simeq \sum_{n=1}^N\{-lnq(\vec{x}_n|\vec{\theta})+lnp(\vec{x}_n)\}\),第二项独立于\(\vec{\theta}\),第一项是利用训练集计算的分布\(q(\vec{x}|\vec{\theta})\)下\(\vec{\theta}\)的负对数似然函数。因此最小化KL散度等价于最大化似然函数。考虑两个变量集合\(\vec{x}\)和\(\vec{y}\)的联合分布\(p(\vec{x},\vec{y})\),若变量集合相互独立,则它们的联合分布会分解成边际分布的乘积:\(p(\vec{x},\vec{y})=p(\vec{x})p(\vec{y})\)。若变量不独立,则我们可以通过考虑联合分布和边际分布乘积之间的KL散度来了解它们是否“接近”独立。\(I[\vec{x},\vec{y}]=KL(p(\vec{x},\vec{y})||p(\vec{x})p(\vec{y}))=-\int\int p(\vec{x},\vec{y})ln(\frac{p(\vec{x})p(\vec{y})}{p(\vec{x},\vec{y})})d\vec{x}d\vec{y}\)称作\(\vec{x}\)和\(\vec{y}\)之间的互信息。从KL散度的属性来看,\(I[\vec{x},\vec{y}]\ge 0\),等号成立当且仅当\(\vec{x}\)和\(\vec{y}\)独立。使用概率的加和和乘积规则:互信息和条件熵有关,\(I[\vec{x},\vec{y}]=H[\vec{x}]-H[\vec{x}|\vec{y}]=H[\vec{y}]-H[\vec{y}|\vec{x}]\)。因此,我们可以把互信息看作是\(\vec{x}\)的不确定性的减少量reduction(通过告诉\(\vec{y}\)的值,反之亦然)。从贝叶斯视角来看,可将\(p(\vec{x})\)看作是\(\vec{x}\)的先验分布,\(p(\vec{x}|\vec{y})\)看作是后验分布(在观测到新数据\(\vec{y}\)之后)。互信息因此表示的是由于新观测\(\vec{y}\)导致的\(\vec{x}\)的不确定性的减少
代码实现
- 链接
- 多项式曲线拟合
- 训练集和测试集生成
- 多项式特征变换
- 模型实现:LinearRegression、RidgeRegression(正则化)、BayesianRegression(贝叶斯方法)
- 指标定义:rmse
原书存疑的地方
- P30公式1.65的指数项以及公式1.67
- P31公式1.69-1.72的推导
- P47公式1.90的推导
- P54公式1.109的推导


