矩阵连乘问题

　　今天算法课讲到了矩阵连乘问题，所以再来复习一下。

　　讲到矩阵连乘问题就不得不讲一讲动态规划。动态规划就是将问题分解为若干个子问题，先将子问题求解，最后在从子问题的解中得到原问题的解。这样看来动态规划好像和分治法相差无几，但是两者还是有着一些差别的，分治法分解的子问题中，子问题互相之间是没有联系的，就是子问题是互相独立的，但是动态规划则不同，子问题之间是有联系的，甚至同一个子问题要被求解多次，所以这也是动态规划和分治法的区别。

　　动态规划求解一般有四个步骤：

　　（1）找出最优解性质，并刻画最优解结构特征。

　　（2）递归的定义最优值。

　　（3）以自底向上的方式计算最优值。

　　（4）根据计算出来的最优值，构造最优解。

　　矩阵连乘问题就是很好的体现了动态规划的思想，这里也是讲矩阵连乘作为讲解动态规划的例子。矩阵连乘问题就是有若干矩阵，将他们相乘的时候因为相乘的次序的不同，相乘时计算的次数也是不同的。比如A1（10*100），A2（100*5）,A3（5*50）三个矩阵，相乘次序分别为（（A1*A2）A3）和（A1（A2*A3））时，矩阵相乘的次数分别为7500和75000，所以我们需要找到相乘次数最少的矩阵相乘次数（最优值）和矩阵相乘次序（最优解）。这就是算法的目的。

　　问题还是比较好理解的，刚开始先用一下我们之前的递归分治方法尝试做一下，发现也是可以做，但是越做到后面越会发现，同一个子问题我们会连续求解很多次。能不能将子问题都存储起来，需要时直接查找呢？这个就是动态规划对于本题的解题思路。将子问题存储起来，需要时直接查找，这样就降低了计算次数。

 

　　大概思路解决了，也找出了最优解的性质，下面我们就递归的求出最优值。要讲最优值，就一定要了解最优子结构性质的公式。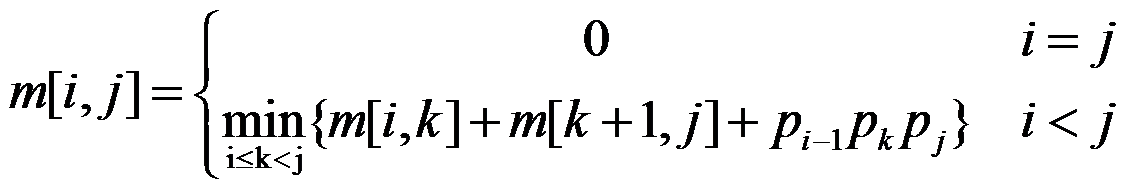

m[i,j]为存储最优值的二维数组，i和j分别代表矩阵的开始和结束。如m[1,6]就表示第一个矩阵到第六个矩阵相乘的最优值。因为单个矩阵相乘无意义，所以当i等于j时，m[i,j]为零。这个公式还是很好理解的，k表示矩阵相乘的断点。前面讲到矩阵相乘的重要之处是找到合适的次序，找次序其实就是找断点。上一个例子就是找到了A2这个断点，并且断点的位置只能在i到j之间。所以，现在也求出了最优值的递归公式。

　　计算最优值也是很简单的，先将底下的子问题计算结果（就是两个矩阵相乘的最优值，并且唯一），最后在利用递归公式求解出上面的子问题。总体的计算最优值的思路就是这样。算出最优值后，构造最优解也就很简单了。遇到的一些问题下面在具体谈。下面粘贴代码。

import java.util.Scanner;

public class demo5 
{
	static int m[][]=new int[50][50];//存放子问题的最优解
	static int s[][]=new int[50][50];//存放子问题的最佳断点
	public static void jzlc(int p[],int m[][],int s[][],int n)
	{
		for(int r=2;r<=n;r++)//矩阵连乘的个数
		{
			for(int i=1;i<=n-r+1;i++)//i为开始的矩阵，小于n-r+1，因为n-r+1+r=n+1
			{
				int j=i+r-1;//j为当前循环的最后的一个矩阵
				m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j];//这个为最佳断点为i时的公式
				s[i][j]=i;
				for(int k=i+1;k<j;k++)//寻找最佳断点
				{
					
					int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
					if(t<m[i][j])
					{
						m[i][j]=t;
						s[i][j]=k;
					}
				}
			}
		}
	}
	public static void dy(int i,int j,int s[][])//递归求出答案，并打印
	{
		if(i==j) return;
		dy(i, s[i][j], s);
		dy(s[i][j]+1, j, s);
		System.out.print("Multipy A" + i + "," + s[i][j]);
        System.out.println(" and A" + (s[i][j]+1) + "," + j);
	}
	public static void main(String args[])
	{
		//6 30 35 15 5 10 20 25          输入
		System.out.println("请输入矩阵相乘的矩阵个数");
		Scanner reader = new Scanner(System.in);
		int n=reader.nextInt();
		int p[]=new int[n+1];//存放矩阵的行和列
		System.out.println("请依次输入矩阵的行和烈（如A*B，A=20*30，B=30*40，即输入20 30 40)");
		for(int i=0;i<n+1;i++)
			p[i]=reader.nextInt();
		jzlc(p, m, s, n);
		for(int i=0;i<=n;i++)//打印存储最优值和最优解的数组，这里要注意i和j的对于数组的位置以及for循环的结束条件
		{
			for(int j=0;j<=n;j++)
			{
				System.out.print(m[i][j]+" ");
			}
			System.out.println();
		}
		System.out.println();
		System.out.println();
		for(int i=0;i<=n;i++)
		{
			for(int j=0;j<=n;j++)
			{
				System.out.print(s[i][j]+" ");
			}
			System.out.println();
		}
		dy(1, n, s);//打印结果
	}
}

　　上面就是具体的实现代码，期间也没有遇到特别的问题，代码的实现也是很顺畅，但是在结束时遇到了我没有办法理解的问题，就是数组中i和j的位置，这里我想了很久，还是没有想明白。后来感觉可能故意写成这个样子，这样算法的实现者不用太花心思纠结在i和j的位置上面。我后来想过将主体代码中i和j减去对应的值，这样整个最优值数组打印的时候就是大家能够接受的结果了，但是后来又发现在构造最优解的时候估计会遇到混乱的问题。这里也不纠结了，大体没有毛病就直接略过了。

　　下面讲一讲最优解的构造，这里代码中就两个数组m和s，分别存储最优值和最佳断点。具体的细节都在注释了。s[i,j]存储的就是矩阵i到j相乘的最佳断点，因为i=j时无意义，所以直接为0，在数组初始化的时候可以置为零，也可以不用管（毕竟一直没有动）。了解了各个数组的维度的意思，构造最优解也就没什么难处了。这里要注意求最优解的时候用到了递归（比较简单和好想）。剩下也就没什么了。结束。