洛谷 1436 棋盘分割

一道经典的DP题目，应该并没有提高＋拉莫难。。。。。。。。。。。。。。。。。。。。。

思路：

搞懂题意后(这点也很重要),我们首先考虑棋盘的分割情况，不难发现：

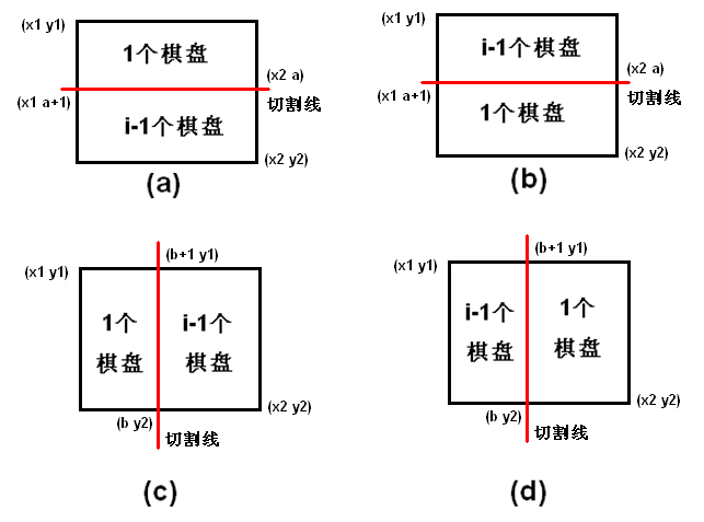
然后我们考虑状态的设计和转移：

AC代码吧:

 

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>

using namespace std;

int read()
{
    int x = 0;
    int k = 1;
    char c = getchar();
    while (c > '9' || c < '0') 
        if (c == '-') c = getchar(), k = -1;
        else c = getchar();
    while (c >= '0' && c <= '9') 
        x = (x << 1) + (x << 3) + (c ^ 48),
        c = getchar();
    return k * x;
}

int n, b, x;
int a[10][10];
int s[10][10];
int dp[10][10][10][10][17];

int calc(int x1, int y1, int x2, int y2)
{
    return s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1];
}

int main()
{
    n = read();
    for (int i = 1; i <= 8; ++i)
        for (int j = 1; j <= 8; ++j)
        {
            if (j == 1) b = 0;
            a[i][j] = read();
            b += a[i][j];
            s[i][j] = s[i - 1][j] + b;
        }
    for (int i = 1; i <= 8; ++i)
        for (int j = 1; j <= 8; ++j)
            for (int o = i; o <= 8; ++o)
                for (int k = j; k <= 8; ++k)
                    dp[i][j][o][k][0] = calc(i, j, o, k),
                    dp[i][j][o][k][0] *= dp[i][j][o][k][0];
    for (int p = 1; p < n; ++p)
        for (int i = 1; i <= 8; ++i)
            for (int j = 1; j <= 8; ++j)
                for (int o = i; o <= 8; ++o)
                    for (int k = j; k <= 8; ++k)
                    {
                        int minn = (1 << 30) + 5555555;
                        for (int l = j; l < k; ++l)
                            minn = min(minn, min(dp[i][l + 1][o][k][0] + dp[i][j][o][l][p - 1], dp[i][l + 1][o][k][p - 1] + dp[i][j][o][l][0]));
                        for (int l = i; l < o; ++l)
                            minn = min(minn, min(dp[l + 1][j][o][k][0] + dp[i][j][l][k][p - 1], dp[l + 1][j][o][k][p - 1] + dp[i][j][l][k][0]));
                        dp[i][j][o][k][p] = minn;
                    }
    printf("%d", dp[1][1][8][8][n - 1]);
                        
             
}