回溯算法-子集组合排列分割

本文分享一些自己在刷回溯算法-子集组合排列分割时总结的套路。

一、回溯算法和二叉树的联系

1. 回溯算法本质上是决策树的选择和撤销过程，所以也属于二叉树。
2. 回溯算法框架中会出现for循环中嵌套递归，for是广度搜索，递归是深度搜索；在二叉树中，经常会有traverse(root.left)和traverse(root.right)，其实这里是将for循环给具体写成了两个递归函数进行广度搜索，然后递归函数进行深度搜索。
3. 回溯算法放到二叉树中说，相当于在前序位置和后序位置进行操作。

二、回溯算法分类

分类规则：原数组中的元素是否重复 | 数组中的元素是否可以复用

1. 元素无重复并且不可复用

相关题目参考LeetCode78、77、46：

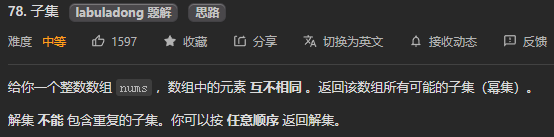
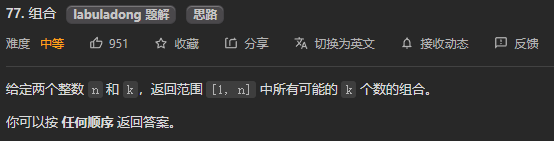
2. 元素有重复并且不可复用

相关题目参考LeetCode90、40、47：

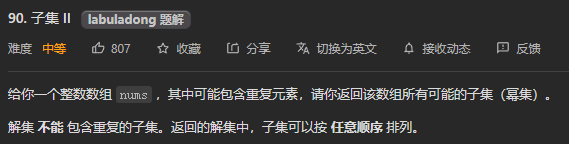
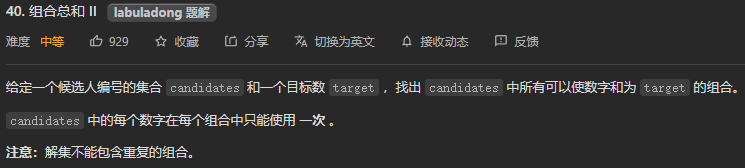
3. 元素无重复并且可以复用

相关题目参考LeetCode39：

三、子集组合排列模块化

本节将子集组合排列模块化，在以后做题时根据题目要求选取模块组装即可，需要做过一些子集组合排列相关回溯题目，对其有一定理解。

1. 回溯函数基本框架

List<List<Integer>> res = new LinkedList<>();
LinkedList<Integer> track = new LinkedList<>();
void backtrack(arg...) {
    //根据条件将路径加入结果集
    if(条件判断) {
        res.add(new LinkedList<>(track));
        return;
    }
    for(循环条件) {
        track.add(数值);
        backtrack(arg...);
        track.removeLast();
    }
}

2. 模块1：if(条件判断)

子集：求全部的子集，不需要条件判断
组合：需要条件判断，一般判断是track.size() == k即符合组合大小K的路径才会添加到结果集
排列：需要条件判断，一般判断是track.size() == nums.length即将数组中的元素全部添加的路径才会添加到结果集
分析：组合和排列的判断条件本质上是一样的，都是取某一层的结果。

3. 模块2：for(循环条件)

子集：for(int i=start; i<nums.length; i++) + backtrack(nums,i+1)
组合：for(int i=start; i<nums.length; i++)/for(int i=start; i<nums.length-(k-track.size())+1; i++) + backtrack(nums,i+1)
排列：for(int i=0; i<nums.length; i++) + if(used[i]) {continue;}
分析：for循环的功能：1.遍历数组 2.在子集和组合问题和backtrack(nums,i+1)配合防止元素被重复使用。 3.在排列问题中和if(used[i]) {continue;}配合防止重复选择

4. 模块3：arg...参数列表

子集：(1)表征数组：int[] nums或者int n (2)表征start：int start
组合：(1)表征数组：int[] nums或者int n (2)表征start：int start (3)表征取第几层集合([]集合是第一层)：int k
排列：(1)表征数组：int[] nums

5. 模块4：假设元素可以重复

子集：(1)Arrays.sort(nums)：排序，让相同的元素靠在一起 (2)在for循环中假如if(i>start && nums[i] == nums[i-1]) {continue;}：i>start使nums[i-1]存在；nums[i] == nums[i-1] 跳过相同的元素
组合：同子集
排列：跟子集略有不同：if(i>start && nums[i] == nums[i-1] && !used[i-1]) {continue;}：新增!used[i-1]是为了固定元素的相对顺序，防止出现重复结果

6. 模块5：假设元素可以复用

此模块与模块2+4相反，模块2的条件都是为了元素不被复用
子集：backtrack(nums,i+1)改为backtrack(nums,i)，且不加模块4的条件
组合：同子集
排列：去掉used剪枝逻辑

7. 总结

子集和组合可以归为一类，backtrack(nums,i+1)是防止同一元素被多次使用，if(i>start && nums[i] == nums[i-1]) 是防止出现重复的结果。
排序单独一类：if(used[i]) {continue;}是防止同一元素被多次使用，!used[i-1]是防止出现重复结果。
排序实则是对子集和组合结果的进一步划分，所以比子集组合的条件更加苛刻。

四、组合的变种-分割问题

组合中相同层不同枝杈之间都依次取一个数，分割问题则是相同层不同枝杈之间依次取1、2、3...n个数，仅这里不同。

究极奥义

1. 回溯算法通常都是for循环+backtrack嵌套
2. for循环代表横向宽度，同时也是横向遍历的逻辑，比如说，track.add(i),i其实是有循环的，start(或者0)<=i<=nums.length。
3. backtrack(nums,i/i+1)代表竖向遍历的深度，同时也是竖向遍历的逻辑。
4. track.add(?)：?可以调整同一层不同枝杈之间的逻辑，其实是你每一个分支树要取到什么，以leetcode70题为例，第一层你每个分支要取的其实就是i;以leetcode131题为例，第一层你每个分支要取的其实就是s.substring(start,i+1);然后第2-n层均和第一层逻辑一样，所以for循环是保证每一层中每一枝杈的逻辑，这里就可以看到你每一层每一条枝杈是怎么取值的。
5. backtrack(?)：?可以调整每一条枝杈不同层之间的逻辑，i+1则保证了一条枝杈每一层和每一层之间的相对顺序并且使得第二层取不到第一层取过得数，而全排列一般是i,因为排序按列不同的顺序是不同的结果。
6. 排列中靠used数组去让第二层取不到第一层取过得数。

超究极奥义

组合子集分割问题，如果你不想让第二层用第一层的用过的数据，backtrack(?)中?就是i+1；如果要复用，就把该条件去掉。同时i+1也保证了不同元素之间的相对顺序，如果要保证同样元素之间的相对顺序，就要加nums[i] == nums[i-1]，continue
全排列问题，本身就是考虑不同的顺序有几种结果，所以不能直接backtrack(i+1),只能用used数组去保证第二层不用第一层的数据，如果要复用，就将该条件去掉；如果要保证同样元素之间的相对顺序，就要加nums[i] == nums[i-1] + !used[i-1] + continue
return是每遍历完一个小枝杈然后返回到原始的位置，本来应该返回上一级，但是上一级会继续返回，直到返回到最初。

题目链接

leetcode-78：子集
leetcode-77：组合
leetcode-46：全排列
leetcode-90：子集II
leetcode-40：组合总和II
leetcode-47：全排列II
leetcode-39：组合总和

声明：本文章参考了东哥的算法小抄，随笔中有很多地方都没有都没有具体解释，主要是作为自己的回顾随笔，如果有不清楚的，可以先看东哥的算法小抄。