博客作业04--树
1.学习总结
1.1树结构思维导图
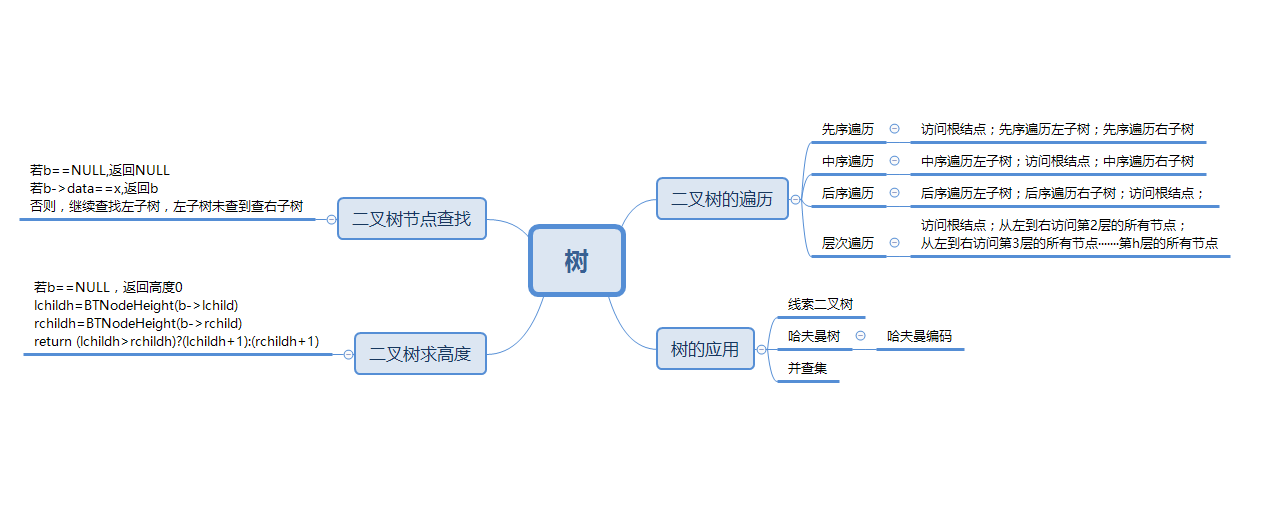
1.2 树结构学习体会
树是一种非线性结构,在现实中用于描述层次关系的一种结构,比如操作系统的文件系统、Internet中的DNS(域名系统)、人类的族谱等,在计算机领域中运用于编译器语法结构、数据库系统、人工智能、数据挖掘算法。在学习树结构的过程中,遇到了不少困难,对于非线性结构,刚开始接触的我还是比较难以理解,而且在树的一些操作中经常运用递归算法,而我对于递归算法还是不熟,所以经常不知道该如何解题。
2.PTA实验作业
2.1.1 题目:jmu-ds-表达式树
2.1.2 设计思路
//建树函数InitExpTree
建字符栈op,树结点栈stacktree
遍历数组str
当str[i]是操作数
建值为str[i]树结点,入树结点栈stacktree
当str[i]为运算符
while(op栈顶优先级比str[i]高)
op栈顶出栈,stacktree出栈两个元素
这两个元素分别为op栈顶元素的左右孩子结点
树结点入栈
当op栈顶优先级比str[i]低
str[i]入栈
当op栈顶优先级与str[i]相等
op栈顶出栈
将op栈中还有的元素继续和树结点栈stacktree中的元素建立树
//计算表达式函数EvaluateExTree
后序遍历二叉表达式树,获得后缀表达式,存入数组postexp中
计算后缀表达式值,并返回
2.1.3 代码截图

2.1.4 PTA提交列表说明
第一次提交时出现答案错误,经过多次测试数据以及在纸上模拟建树过程,发现建树过程中左右子树的反了,经过调整,还有一个点错误,就是除0错误,请教同学,知道在分母为0的情况下使用exit(0)终止程序即可。
2.2.1 题目:根据后序和中序遍历输出先序遍历
2.2.2 设计思路
//建树函数CreatBinTree(int *last,int *in,int n)
建根结点s,定义指针p
n为0时为空栈,返回NULL
根结点数据为last[n-1]
在中序序列中找出根结点所在位置
左子树结点个数k=p-in
s->Left=CreatBinTree(last,in,k);
s->Right=CreatBinTree(last+k,p+1,n-k-1);
返回s
2.2.3 代码截图
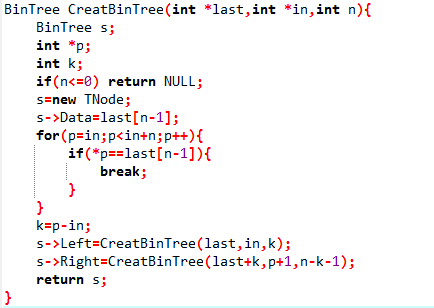
2.2.4 PTA提交列表说明
本题一遍就过,无错误提交
2.3.1 题目:二叉树叶子结点带权路径长度和
2.3.2 设计思路
//计算WPL函数wpl(BTree BT)
建队列q
定义变量wpl,deep
定义BTree型变量lastNode,newlastNode
lastNode初始化为根结点,newlastNode为空
根结点入队列q
当队列不为空
出栈一个元素t
当t为叶结点时
累加权值wpl
当t左孩子不为空
左孩子入队列,置newlastNode为t->lchild
当t右孩子不为空
右孩子入队列,置newlastNode为t->rchild
当t与lastNode相等时
更新lastNode为newlastNode,deep+1
返回wpl
2.3.3 代码截图

2.3.4 PTA提交列表说明
提交时有一个点没过,于是我就去多试了几组数据,发现有些情况答案错误,仔细检查了一下代码,发现建树函数存在问题,当空结点不为叶结点时建出来的树会发生混乱,后来把空结点也进队列,调整了一下就可以了。
3.截图本周题目集的PTA最后排名
3.1 PTA排名
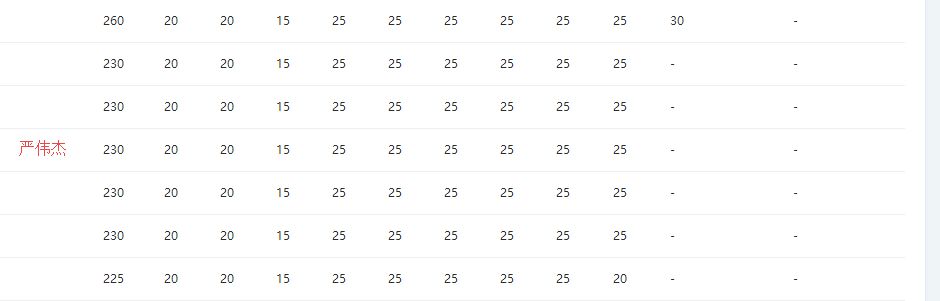
3.2 我的得分:
230
4. 阅读代码
题目:哈夫曼编码解码
#include<iostream>
#include<string>
using namespace std;
struct Node
{
double weight;
string ch;
string code;
int lchild, rchild, parent;
};
void Select(Node huffTree[], int *a, int *b, int n)//找权值最小的两个a和b
{
int i;
double weight = 0; //找最小的数
for (i = 0; i <n; i++)
{
if (huffTree[i].parent != -1) //判断节点是否已经选过
continue;
else
{
if (weight == 0)
{
weight = huffTree[i].weight;
*a = i;
}
else
{
if (huffTree[i].weight < weight)
{
weight = huffTree[i].weight;
*a = i;
}
}
}
}
weight = 0; //找第二小的数
for (i = 0; i < n; i++)
{
if (huffTree[i].parent != -1 || (i == *a))//排除已选过的数
continue;
else
{
if (weight == 0)
{
weight = huffTree[i].weight;
*b = i;
}
else
{
if (huffTree[i].weight < weight)
{
weight = huffTree[i].weight;
*b = i;
}
}
}
}
int temp;
if (huffTree[*a].lchild < huffTree[*b].lchild) //小的数放左边
{
temp = *a;
*a = *b;
*b = temp;
}
}
void Huff_Tree(Node huffTree[], int w[], string ch[], int n)
{
for (int i = 0; i < 2 * n - 1; i++) //初始过程
{
huffTree[i].parent = -1;
huffTree[i].lchild = -1;
huffTree[i].rchild = -1;
huffTree[i].code = "";
}
for (int i = 0; i < n; i++)
{
huffTree[i].weight = w[i];
huffTree[i].ch = ch[i];
}
for (int k = n; k < 2 * n - 1; k++)
{
int i1 = 0;
int i2 = 0;
Select(huffTree, &i1, &i2, k); //将i1,i2节点合成节点k
huffTree[i1].parent = k;
huffTree[i2].parent = k;
huffTree[k].weight = huffTree[i1].weight + huffTree[i2].weight;
huffTree[k].lchild = i1;
huffTree[k].rchild = i2;
}
}
void Huff_Code(Node huffTree[], int n)
{
int i, j, k;
string s = "";
for (i = 0; i < n; i++)
{
s = "";
j = i;
while (huffTree[j].parent != -1) //从叶子往上找到根节点
{
k = huffTree[j].parent;
if (j == huffTree[k].lchild) //如果是根的左孩子,则记为0
{
s = s + "0";
}
else
{
s = s + "1";
}
j = huffTree[j].parent;
}
cout << "字符 " << huffTree[i].ch << " 的编码:";
for (int l = s.size() - 1; l >= 0; l--)
{
cout << s[l];
huffTree[i].code += s[l]; //保存编码
}
cout << endl;
}
}
string Huff_Decode(Node huffTree[], int n,string s)
{
cout << "解码后为:";
string temp = "",str="";//保存解码后的字符串
for (int i = 0; i < s.size(); i++)
{
temp = temp + s[i];
for (int j = 0; j < n; j++)
{
if (temp == huffTree[j].code)
{
str=str+ huffTree[j].ch;
temp = "";
break;
}
else if (i == s.size()-1&&j==n-1&&temp!="")//全部遍历后没有
{
str= "解码错误!";
}
}
}
return str;
}
int main()
{
//编码过程
const int n=5;
Node huffTree[2 * n];
string str[] = { "A", "B", "C", "D", "E"};
int w[] = { 30, 30, 5, 20, 15 };
Huff_Tree(huffTree, w, str, n);
Huff_Code(huffTree, n);
//解码过程
string s;
cout << "输入编码:";
cin >> s;
cout << Huff_Decode(huffTree, n, s)<< endl;;
system("pause");
return 0;
}
一般情况下,以字符:‘0’与‘1’表示。编码的实现过程很简单,只要实现哈夫曼树,通过遍历哈夫曼树,这里我们从每一个叶子结点开始向上遍历,如果该结点为父节点的左孩子,则在字符串后面追加“0”,如果为其右孩子,则在字符串后追加“1”。结束条件为没有父节点。然后将字符串倒过来存入结点中。
5. 代码Git提交记录截图