拓扑排序及其实际应用

　　最近在做实际项目中遇到了一个问题，如何判断一个层级结构的图是否存在循环引用。刚开始想到了方法是用递归进行判断，后来想到大学学过的拓扑排序可以解决该问题，于是翻了下数据结构这本书，阅读了园友的文章，根据自己的理解写下了这篇随笔。

阅读目录

拓扑排序介绍
问题引入及算法实现
本章总结

拓扑排序介绍

　　百度百科定义：

　　对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

　　上面的定义看完可能不知道是什么意思，举两个实际的例子就明白了。

1.大学课程排序

　　大学课程的学习是有先后顺序的，C语言是基础，数据结构依赖于C语言，其它课程也有类似依赖关系。这样的一个课程安排是怎么实现的呢？

　　2.VS项目编译顺序

假设VS中有三个项目A,B，C，它们的关系如下图。VS编译器是如何判断三个项目的编译顺序的呢？

回到顶部

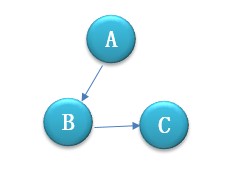
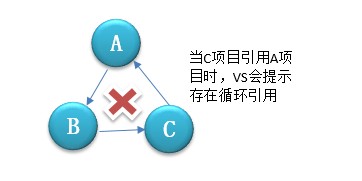
问题引入及算法实现

　　这次实际项目中碰到的问题可以归纳为控件联动选择，即常见的省份，城市，地区联动。为了实现通用的下拉连dog，设计了一套表结构，最终保存数据如下。

看到这里也许你不明白这个和拓扑排序能扯上什么关系，假如省份下拉又依赖于地区下拉，那这样就会形成一个死循环。为了避免这样的情况需要在数据保存时，校验是否存在闭环。

下面给出，解决上述问题的两种算法。

1.递归判断

　 步骤如下

(1)找当前节点的父级节点（也可以叫依赖的节点）

　　(2)父级节点不为为空且不等于当前节点自己，则寻找父级节点对应的父级节点

(3)重复1，2。最终找到的节点=自己，则存在闭环，否则不存在

代码实现

首先定义了一个类似的结构

    public class Node
    {
        /// <summary>
        /// 当前节点ID
        /// </summary>
        public int Key { get; set; }

        /// <summary>
        /// 父级节点ID
        /// </summary>
        public int? Parent { get; set; }
    }

/// <summary>
    /// 递归判断是否存在循环引用
    /// </summary>
    public class RecursionSort
    {
        /// <summary>
        /// 递归判断是否存在循环引用
        /// </summary>
          public  static bool CheckRecursion(List<Node> list)
        {
            foreach (var node in list)
            {
                if (RecursionSort.CheckRecursion(node.Key,node, list))
                {
                    return true;
                }
            }
            return false;
        }

        /// <summary>
        /// 递归判断是否存在循环引用
        /// </summary>
        /// <param name="list"></param>
        /// <returns></returns>
        private static bool CheckRecursion(int key,Node curNode, List<Node> list)
        {
            if (curNode.Parent == key)
            {
                return true;
            }
            //寻找父级节点对应的父级节点信息
            if (curNode.Parent != null)
            {
                Node pNode = list.Where(e => e.Key == curNode.Parent).FirstOrDefault<Node>();
                return CheckRecursion(key,pNode, list);
            }
            return false;
        }
    }

        static void Main(string[] args)
        {
            //递归判断
            List<Node> list = new List<Node>();
            list.Add(new Node { Key=1,Parent=2});
            list.Add(new Node { Key = 2, Parent = 1 });
            list.Add(new Node { Key = 3, Parent = 2 });
            Console.WriteLine(RecursionSort.CheckRecursion(list));
            Console.Read();
        }

2.拓扑排序

步骤如下

(1) 从有向图中选择一个出度为0(即不依赖任何其它节点)的顶点并且输出它。
　　 (2) 从图中删去该顶点，并且删去该顶点的所有边。
(3) 重复上述两步，直到剩余的图中没有出度为0的顶点。

我们来看一下上面举的VS项目编译顺序列子按照上述算法的演示过程

第一步选择 C节点

第二步选择 B节点

至此完成了整个排序C，B，A 即先编译C项目，再编译B项目，最后编译A项目

代码实现如下

    /// <summary>
    /// 拓扑节点类。
    /// </summary>
    public class TopologicNode<T>
    {
        /// <summary>
        /// 获取或设置节点的键值。
        /// </summary>
        public T Key { get; set; }

        /// <summary>
        /// 获取或设置依赖节点的键值列表。
        /// </summary>
        public List<T> Dependences { get; set; }
    }

 /// <summary>
    /// 拓扑排序类。
    /// </summary>
    public class TopologicSort
    {
        /// <summary>
        /// 拓扑顺序。
        /// </summary>
        /// <typeparam name="TKey">节点的键值类型。</typeparam>
        /// <param name="list">一组节点。</param>
        /// <returns>拓扑序列。</returns>
        /// <exception cref="InvalidOperationException">如果存在双向引用或循环引用，则抛出该异常。</exception>
        public static List<T> OrderBy<T>(List<TopologicNode<T>> list)
        {
            if (list == null)
            {
                throw new ArgumentNullException("参数空异常");
            }
            List<T> listResult = new List<T>();
            while (list.Count > 0)
            {
                //查找依赖项为空的节点
                var item = list.FirstOrDefault(c => c.Dependences == null || c.Dependences.Count == 0);
                if (item != null)
                {
                    listResult.Add(item.Key);

                    //移除用过的节点，以及与其相关的依赖关系
                    list.Remove(item);
                    foreach (var otherNode in list)
                    {
                        if (otherNode.Dependences != null)
                        {
                            otherNode.Dependences.Remove(item.Key);
                        }
                    }
                }
                else if (list.Count > 0)
                {
                    //如果发现有向环，则抛出异常
                    throw new InvalidOperationException("存在循环引用");
                }
            }
            return listResult;
        }
    }

 //拓扑排序
            //节点3依赖于2和1节点
            list.Add(new Node { Key = 3, Parent = 1 });

            List<TopologicNode<int>> listTopologicNode = new List<TopologicNode<int>>();
            //构建排序节点

            var group = (from p in list
                         group p by p.Key into g
                         select g);

            foreach (var g in group)
            {
                TopologicNode<int> node = new TopologicNode<int>();
                node.Key = g.Key;
                node.Dependences = new List<int>();
                foreach (Node value in g)
                {
                    if (value.Parent != null)
                    {
                        node.Dependences.Add(value.Parent.GetValueOrDefault());
                    }
                }
                listTopologicNode.Add(node);
            }

            try
            {
                List<int> result = TopologicSort.OrderBy<int>(listTopologicNode);
                result.ForEach(e => {
                    Console.WriteLine(e);
                });
            }
            catch (Exception ex)
            {
                Console.WriteLine(ex.Message);
            }