机械设计名词之内部边界IB及外部边界OB

       机械设计并不仅仅是会3D画图，还需要做到出一份正确的、合理的2D加工图。那么在设计的过程中需要理解、解决设计过程中遇到的一些基本问题，装配就需要给出合理的公差，那么如何给出正确、合适的公差呢？当然是需要通过计算得到最大间隙、最小间隙，满足设计要求才算是一个正确的设计。

 首先给大家引入两个基本概念：

最大实体状态MMC和最小实体状态LMC

************************************************************************************************

1. 最大实体状态（MMC）：是指尺寸形体在规定的尺寸界限内具有最多材料时的状态(即孔的最小直径，轴的最大直径)。

2. 最小实体状态（LMC）：是指尺寸形体在规定的尺寸界限内具有最少材料时的状态(即孔的最大直径，轴的最小直径)。

*************************************************************************************************************

首先MMC和LMC是由尺寸公差来定义的一个固定的状态，适用于尺寸形体，与它们的几何公差无关，也与它们的实际尺寸无关。它们定义了尺寸形体的两个尺寸边界------内部边界（IB）和外部边界（OB）。

*************************************************************************************************************

1. 内部边界Inner Boundary – IB: 是指由形体的最小尺寸(轴类形体是LMC,孔类形体是MMC)减去指定的形位公差及当尺寸公差偏离指定材料状态时补偿形位公差构成的一个最差边界条件。

2. 外部边界 Outer Boundary - OB : 是指由形体的最大尺寸(轴类形体是MMC,孔类形体是LMC)加上指定的形位公差及当尺寸公差偏离指定材料状态时补偿形位公差构成的一个最差边界条件。

**************************************************************************************************************

考虑到零件之间的装配，所以定义尺寸边界。MMC时是零件最难装配的状态，而LMC是零件最易装配的状态。

对于孔轴配合，

孔越小，轴越大，零件就越难装配；

相反，

孔越大，轴越小，零件就越易装配。

因此我们定义MMC是零件最难装配的状态，也就是满足最小装配间隙时的状态；而LMC则反之。

从装配的角度去理解MMC和LMC的定义，对于我们理解下面介绍的更多边界条件会很大的帮助。

下图是对于孔、轴的最大实体状态和最小实体状态的计算：

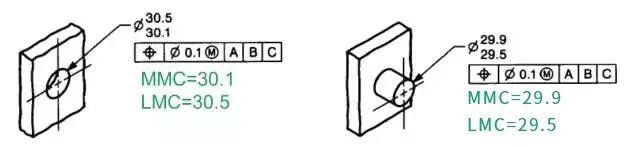
根据MMC和LMC的概念，很容易计算孔和轴的MMC和LMC的边界尺寸。在实际生产过程中装配零件，孔的MMC是它最难装配时的尺寸，也就是它的最小尺寸，即φ30.1；孔的LMC则是它的最大尺寸，即φ30.5。同样，轴的MMC与是它最难装配时的尺寸，即最大尺寸φ29.9；轴的LMC则是它的最小尺寸，即φ29.5。

因此我们知道上面的设计如果不考虑位置度的影响，也就是说只考虑在孔和轴至少有一个没有定位时的装配情况，它保证了φ0.2的最小装配间隙。这个φ0.2的间隙是由孔的MMC（φ30.1）减去轴的MMC（φ29.9）得到的。

从理论上讲，如果孔和轴的MMC都是φ30，那么设计就保证了最小间隙为0的装配条件，因此也是可行的。但这里有个问题，如果孔的实际尺寸是它的MMC即φ30，它没有任何的形状误差，轴的实际尺寸也是它MMC即φ30，但它的直线度不是很好，零件有点弓形，此时这根轴就无法装到这个孔内。实际上当孔和轴的实际尺寸都在MMC时，只要其中任何一个零件有形状误差，那么装配就将无法实现。

*******************************************************************************************************************************

通过以上介绍，我们了解了MMC和LMC，那么边界的实际计算怎么样呢？接下来继续学习：

根据定义，不管是孔类形体还是轴类形体，它的IB都是一个最小的边界，永远是用减法获得的；而OB是一个最大的边界，永远是由加法获得的。

口诀简化为：内减外加

计算公式如下：

IB=最小尺寸-形位公差-最小尺寸时的补偿公差

OB=最大尺寸+形位公差+最大尺寸时的补偿公差

因此我们很容易计算出下例中孔和轴的IB和OB

 

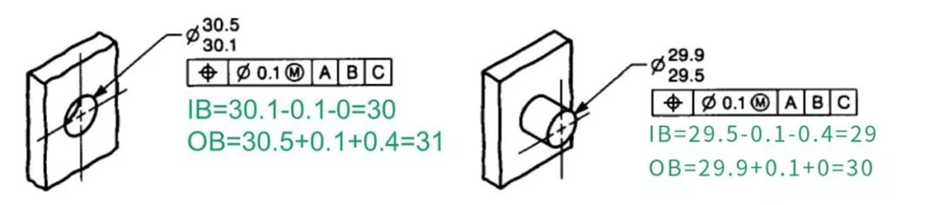
a. IB及OB的形成

那么IB和OB是如何形成的呢？以上图中的孔为例，孔的最小尺寸也就是它的MMC是φ30.1，此时它允许有一个φ0.1的位置度公差，也就是说φ30.1的圆心可以是在φ0.1圆内的任意位置，这样它就构建出一个φ30的最小边界，相当于φ30.1的圆心绕φ0.1圆一周而形成一个最大内切圆，这就是它的内部边界IB。

 

同理，孔的最大尺寸也就是它的LMC是φ30.5，此时它允许有一个φ0.5的位置度公差（0.1的位置度公差加上LMC时0.4的补偿公差），也就是说φ30.5的圆心可以是在φ0.5圆内的任意位置，这样它就构建出一个φ31的最大边界，相当于φ30.5的圆心绕φ0.5圆一周而形成一个最小外接圆，这就是它的外部边界OB。

 

 

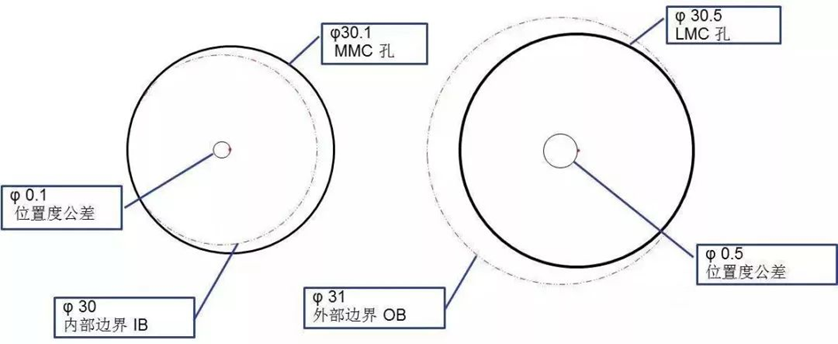
轴类形体的内部边界与外部边界的形成和计算与孔类形体的相似，这里就不多讲了，大家有空时可以按上面的过程分析一下，以加深理解。如果有兴趣，大家还可以思考一下形位公差在LMC时的IB和OB的形成，道理都是一样的。大家只要记住IB用减法，OB用加法不行了。

值得注意的是，在计算IB和OB时，一定要考虑补偿形位公差，一定要搞清楚什么时候有补偿，什么时候没有补偿。

 关于补偿公差这个说法下一篇文章在简要介绍，这里先记住怎么计算IB和OB。

知识不是一天学习完成的，我们一点一点的学习。只要肯努力，一切都有可能。

 

本文参考其他作者的文章进行转载、修改完成的，不作为盈利目的， 仅供学习、交流。

转载请说明转载出处！！！