24暑假集训day5上午

图论

差分约束

有 $𝑛$ 个整数变量 ${𝑥}_1\sim {𝑥}_{𝑛}$。

给定一些形如 ${𝑥}_{𝑖}+𝑐\ge {𝑥}_{𝑗}$ 的限制。问有没有可行解，如有输出方案。

例如 ${𝑥}_1-1\ge {𝑥}_2,{𝑥}_2\ge {𝑥}_3,{𝑥}_3\ge {𝑥}_1$ 就无解。

在单源最短路问题中，如果存在一条 $𝑖\to 𝑗$ 长为 $𝑤$ 的边，在计算 $1$ 号点到每个点的最短路后，一定有 $𝑑𝑖𝑠[𝑖]+𝑤\ge 𝑑𝑖𝑠[𝑗]$。

所以对于每个 ${𝑥}_{𝑖}+𝑐\ge {𝑥}_{𝑗}$ 的限制，可以连边 $(𝑖,𝑗,𝑐)$。

如果图中存在负环，则无解。假如负环节点编号为 $1,2,3,\dots ,𝑘$，那么 ${𝑥}_1\ge {𝑥}_2-{𝑐}_{12}\ge {𝑥}_3-{𝑐}_{12}-{𝑐}_{23}\ge \dots \ge {𝑥}_1-{𝑐}_{12}-{𝑐}_{23}-\dots -{𝑐}_{𝑘1}$，而 ${𝑐}_{12}+{𝑐}_{23}+\dots +{𝑐}_{𝑘1}<0$，所以无解。

如果图中没有负环，则有解。跑完最短路后，令 ${𝑥}_{𝑖}=𝑑𝑖𝑠[𝑖]$ 即可。

如果有 ${𝑥}_{𝑖}+𝑐={𝑥}_{𝑗}$ 的限制，就拆成 ${𝑥}_{𝑖}+𝑐\ge {𝑥}_{𝑗}$ 与 ${𝑥}_{𝑗}-𝑐\ge {𝑥}_{𝑖}$。所以可以连边 $(𝑖,𝑗,𝑐),(𝑗,𝑖,-𝑐)$。

图不连通时，各个连通块可以独立考虑。

差分约束求值

注意到我们可以给每个 ${𝑥}_{𝑖}$ 都加上一个 $\Delta$，并不影响每个限制 ${𝑥}_{𝑖}+𝑐\ge {𝑥}_{𝑗}$。所以无法“求出一组合法解，使得 ${𝑥}_{𝑝}$ 最大 / 最小”。

但是可以“求出一组合法解，使得 ${𝑥}_{𝑝}-{𝑥}_{𝑞}$ 最大 / 最小”。

由于 ${𝑥}_{𝑝}-{𝑥}_{𝑞}$ 最小 $\iff {𝑥}_{𝑞}-{𝑥}_{𝑝}$ 最大，所以我们只考虑让 ${𝑥}_{𝑝}-{𝑥}_{𝑞}$ 最大。

由于 ${𝑥}_{𝑝}-{𝑥}_{𝑞}\le 𝑑𝑖𝑠(𝑞,𝑝)$，所以 ${𝑥}_{𝑝}-{𝑥}_{𝑞}$ 再大也不能比 $𝑑𝑖𝑠(𝑞,𝑝)$ 大。而从 $𝑞$ 点跑一遍最短路后，${𝑥}_{𝑝}-{𝑥}_{𝑞}$ 正好取到 $𝑑𝑖𝑠(𝑞,𝑝)$，所以这就是合法的最大值。此时的 $𝑑𝑖𝑠$ 数组$𝑑𝑖𝑠[𝑖]=𝑑𝑖𝑠(𝑞,𝑖)$就是满足 ${𝑥}_{𝑝}-{𝑥}_{𝑞}$ 最大时合法的解。

如果有 ${𝑥}_{𝑖}\ge 𝑤$ 的限制，就连边 $(𝑖,$起点$,-𝑤)$，因为 $𝑑𝑖𝑠[$起点$]=0$，所以 ${𝑥}_{𝑖}\ge 𝑤$ 相当于 ${𝑥}_{𝑖}-𝑤\ge {𝑥}_{\mathrm{起}\mathrm{点}}=0$ 。

小K的农场

思路:

设 ${𝑦}_{𝑗}$ 为农场 $𝑗$ 的作物单位数。

农场 $𝑏$ 比农场 $𝑐$ 至少多种了 ￥𝑑$ 的作物：${𝑦}_{𝑏}-𝑑\ge {𝑦}_{𝑐}$，连边 $𝑏,𝑐,-𝑑$。

农场 $𝑏$ 比农场 $𝑐$ 至多多种了 $𝑑$ 的作物：${𝑦}_{𝑐}+𝑑\ge {𝑦}_{𝑏}$，连边 $𝑐,𝑏,𝑑$。

农场 $𝑏$ 与农场 $𝑐$ 种植作物一样多：${𝑦}_{𝑏}={𝑦}_{𝑐}$，连边 $𝑏,𝑐,0$,$𝑐,𝑏,0$。

使用 SPFA 判断图中是否有负环。有负环则无解，无负环则有解。

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<map>
#include<vector>
#include<queue>
#include<set>
#include<unordered_map>
#include<bitset>
#include<climits>
#include<cassert>
using namespace std;
const int MAXN=100005;
int n,m,s,dis[MAXN];
bool inqueue[MAXN];
queue<int> Q;
int flag[MAXN];
vector<pair<int,int> > edges[MAXN];
int main(){
	int n,m;
	cin >> n >> m ;
	memset(dis,0x3f,sizeof(dis));
	for(int i=0,u,v,w;i<m;i++){
		int op,a,b,c;
		cin>>op;
		if(op==1){
			cin >> a >> b >> c;
			edges[a].emplace_back(b,-c);
		}else if(op==2){
			cin >> a >> b >> c;
			edges[b].emplace_back(a,c);
		}else{
			cin >> a >> b;
			edges[a].emplace_back(b,0);
			edges[b].emplace_back(a,0);
		}
	}
	for(int i=1;i<=n;i++){
	    edges[0].emplace_back(i,0);
	}
	dis[s]=0;
	Q.push(s);
	inqueue[s]=true;
	while(!Q.empty()){
		int x=Q.front();
		Q.pop();
		inqueue[x]=false;
		for(auto edge:edges[x]){
			if(dis[edge.first]<=dis[x]+edge.second)continue;
			dis[edge.first]=dis[x]+edge.second;
			if(!inqueue[edge.first]){
				Q.push(edge.first);
				flag[edge.first]=flag[x]+1;
				if(flag[edge.first]>n){
					cout<<"No\n";
					return 0;
				}
				inqueue[edge.first]=true;
			}
		}
	}
	cout<<"Yes\n";
	return 0;
}

拓扑排序

对于一个有向无环图，为每个节点 $𝑗$ 分配一个顺序 $or{d}_{𝑗}$，使得对于任意有向边 $𝑣\to 𝑤$，都有 $or{d}_{𝑣}<or{d}_{𝑤}$。

在有环图上无法做到，假设环为 $a_1,a_2,\dots ,a_{𝑛}$，则需要 $ord{a}_1<ord{a}_2<\cdots <ord{a}_{𝑚}<ord{a}_1$，矛盾。

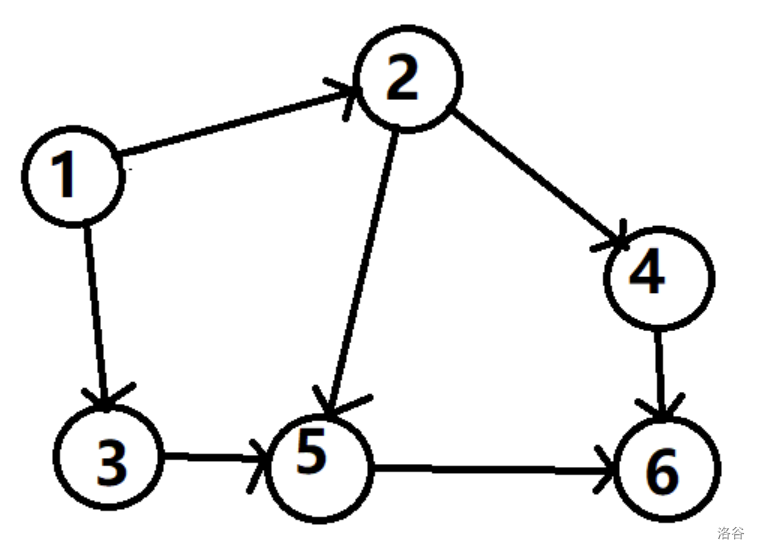
最开始的节点一定不能有入度。所以我们可以每次任选一个没有入度的节点，将其拓扑序置为 $1$。然后删除此节点，递归处理剩下的图（继续找到没有入度的点，将其拓扑序置为 $2，\dots$）。

由于删完节点后，图仍然是 DAG，所以存在合法拓扑序。

换句话说，任选一个没有入度的节点都是合法的。

用一个队列维护所有入度 $=0$ 的点。

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<map>
#include<vector>
#include<queue>
#include<set>
#include<unordered_map>
#include<bitset>
#include<climits>
#include<cassert>
#define int long long
using namespace std;
const int N=100005;

inline int read(){
	int x=0,f=1;
	char ch=getchar();
	while (ch<'0'||ch>'9'){
		if (ch=='-') f=-1;
		ch=getchar();
	}
	while (ch>='0'&&ch<='9'){
		x=x*10+ch-48;
		ch=getchar();
	}
	return x*f;
}
int ord[N], inDegree[N];
int n, m;
queue<int> Q;
vector<int> nextPoints[N];
signed main(){
    cin >> n >> m;
    for(int i=0,u, v; i< m; i++){
        cin >> u >> v;
        nextPoints[u].push_back(v);
        inDegree[v]++;
    }
    for(int i=0;i<n; i++){
        if(inDegree[i]==0){
            Q.push(i);
        }
    }
    int cnt = 0;
    while(!Q.empty()){
        int x=Q.front();
        Q.pop();
        ord[x] = ++cnt;
        for(auto y: nextPoints[x]){
            inDegree[y]--;
            if(inDegree[y]==0){
                Q.push(y);
            }
        }
    }
    return 0;
}

如果原图中存在环，那么这个环以及其能到达的所有点，都不会被删除。

所以可以使用拓扑排序判断有向图是否是 DAG。只需要在结束时判断 $𝑐𝑛𝑡==𝑛?$ 即可。

---

两个相似的问题

要求拓扑序靠前的编号尽量小。即最小化 $𝑜𝑟{𝑑}^{-1}$ 的字典序。

要求编号小的拓扑序尽量靠前。即最小化 $𝑜𝑟𝑑$ 的字典序。

其中 $𝑜𝑟{𝑑}^{(}-1)$ 的意思是 $𝑜𝑟{𝑑}^{-1}[𝑜𝑟𝑑[𝑖]]=𝑖$，即 $𝑜𝑟{𝑑}^{-1}$ $[𝑖]$ 表示拓扑序第 $𝑖$ 位的节点编号。

拓扑序靠前的编号尽量小

普通的拓扑排序每次任选一个 inDegree=0 的节点。现在我们只需要每次取编号最小的节点即可。

用优先队列替换队列维护 inDegree=0 的节点，每次取出编号最小的节点。

编号小的拓扑序尽量靠前

直接做是不可行的，我们不知道删掉哪个点能最快到达 $1$ 号点。

但是我们可以让“编号小的拓扑序尽量靠后”：尽量拖延删除 1 号点的时间，直到不得已再删（此时队列中只有 $1$ 号点）。在此基础上，尽量拖延删除 $2$ 号点，… 也就是每次删除编号最大的点。

然后反向建图即可。反向的拓扑序靠后就是正向的拓扑序靠前。

---

拓扑序计数

给定一张有向无环图，求其合法拓扑序个数。

$𝑛\le 20,𝑚\le \frac{𝑛(𝑛-1)}{2}$

设 $𝑓(𝑆)$ 表示 $𝑆$ 诱导子图的拓扑序个数。

转移时，枚举 $𝑆$ 中拓扑序最靠前的节点 𝑖 ：

$$𝑓(𝑆)={\sum }_{𝑖\in 𝑆,in{d}_{𝑖}=0}𝑓(𝑆-\{𝑖\})$$

其中 ind_𝑖=0 表示 $𝑖$ 在 $𝑆$ 中没有入度（而非整个图中）。

---

次小生成树问题

求次小生成树。（可能与最小生成树边权和相等）

$𝑛\le 1000$

第三小？

---

经过 1 号点的最小环

给定一个有向图，无重边无自环，求经过 $1$ 号点的最小环。

边权非负，$𝑛,𝑚\le {10}^5$。