软考----二叉树

知识图谱

 

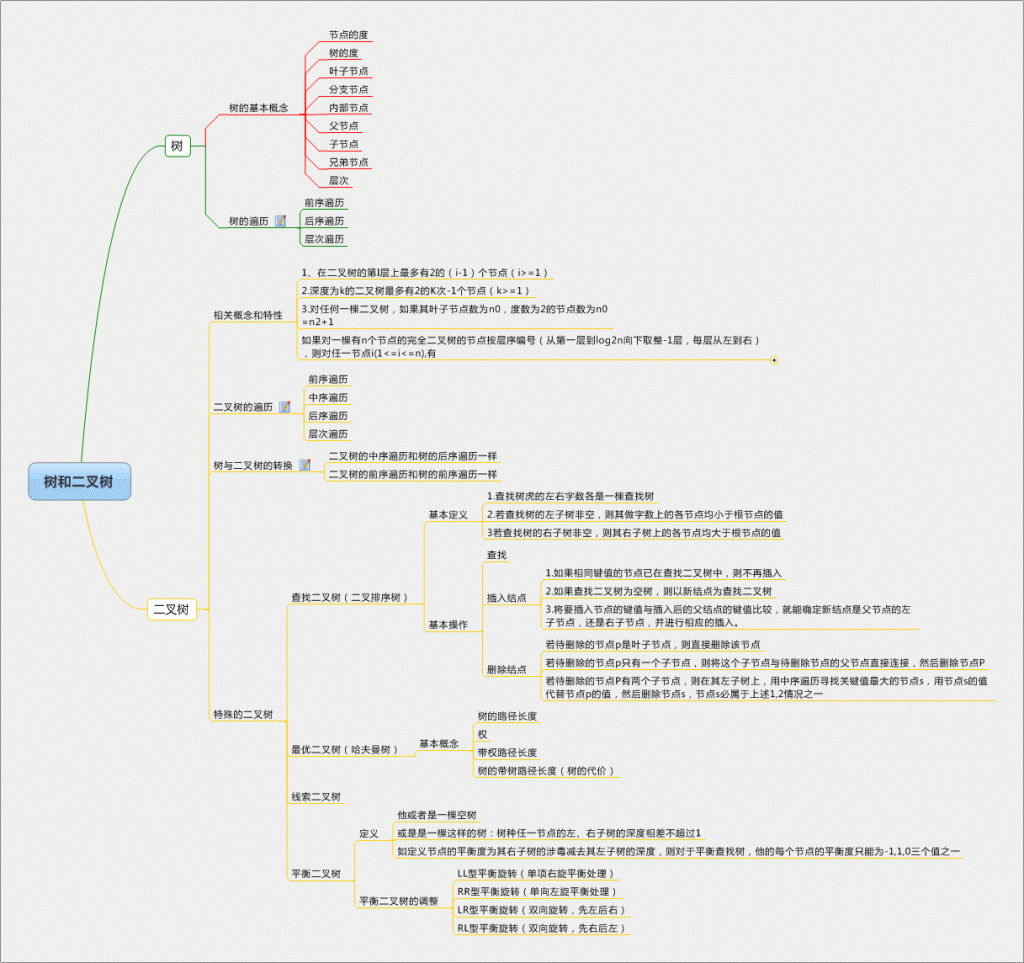
树的基本概念

节点的度：节点具有子树的数量。

 

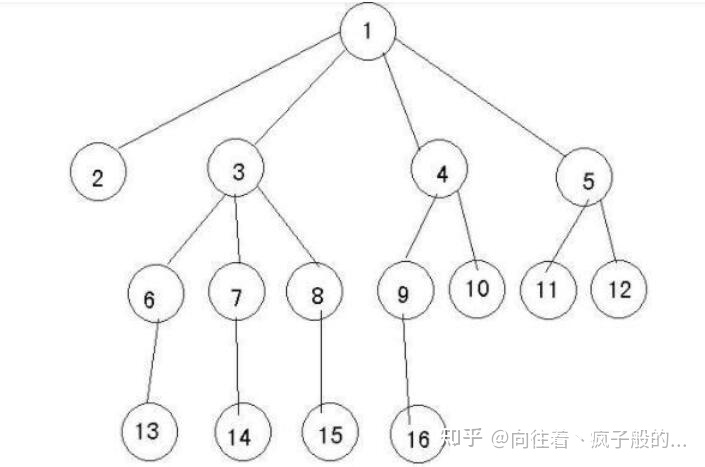
比如①结点的度为4。

树的度：树中各结点最大的度，比如上图树中最大的度为①，那么树的度就是4。

叶子结点：度数为0的结点。

分支结点：度数不为0的结点。

内部结点：度数部位0的结点。

层次：根的层次为0，根的直接左右孩子层次为1，以此类推层次逐渐递增。

树的遍历（前序(根左右),中序(左根右),后序(左右根)）

　　　　　　　　　　　　　　　　　　　　　　　　　　

 

 

 

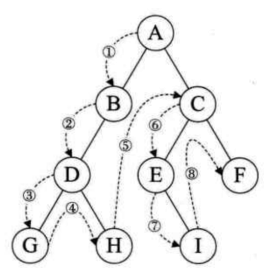
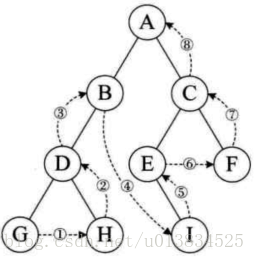
  　　　　　　前序遍历　　　　　　　　　　　　　　　　　　　　　　　　　　　　中序遍历　　　　　　　　　　 　　　　　　　　　　　　　　　　　　后序遍历

 

 　　　　　　　　层序遍历

 

 

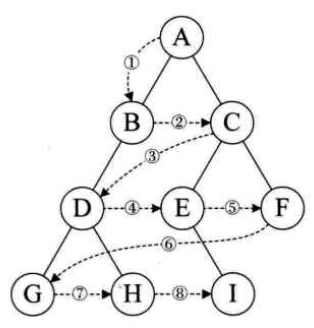
　　上图中

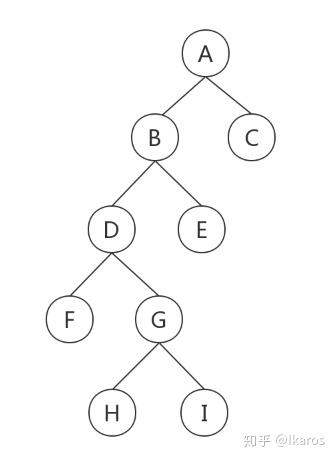
前序遍历A-B-D-F-G-H-I-E-C

中序遍历F-D-H-G-I-B-E-A-C

后序遍历F-H-I-G-D-E-B-C-A

例题1:

已知某二叉树的前序遍历为A-B-D-F-G-H-I-E-C,中序遍历为F-D-H-G-I-B-E-A-C,请还原这颗二叉树。

解题思路：

从前序遍历中，我们确定了根结点为A，在从中序遍历中得出 F-D-H-G-I-B-E在根结点的左边，C在根结点的右边，那么我们就可以构建我们的二叉树的雏形。

 

 

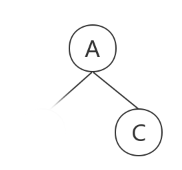
那么剩下的前序遍历为B-D-F-G-H-I-E，中序遍历为F-D-H-G-I-B-E， B就是我们新的“根结点”，从中序遍历中得出F-D-H-G-I在B的左边，E在B的右边，继续构建

 

 

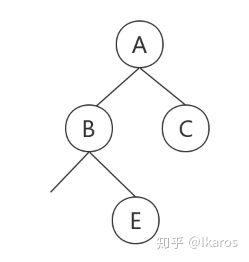
那么剩下的前序遍历为D-F-G-H-I，中序遍历为F-D-H-G-I，D就是我们新的“根结点”，从中序遍历中得出F在D的左边，H-G-I在D的右边，继续构建

 

 

那么剩下的前序遍历为G-H-I，中序遍历为H-G-I，G就是我们新的“根结点”，从中序遍历中得出H在G的左边，I在G的右边，继续构建

例题2：

已知某二叉树的中序遍历为F-D-H-G-I-B-E-A-C,后序遍历为F-H-I-G-D-E-B-C-A,请还原这颗二叉树。

解题思路：

从后序遍历中，我们确定了根结点为A，在从中序遍历中得出 F-D-H-G-I-B-E 在根结点的左边，C在根结点的右边，那么我们就可以构建我们的二叉树的雏形。之后就是新根节点B，FDHGI在根左，E在根右。在之后就是新根D，F根左，HGI根右，然后就差不多了。

和前序和中序还原二叉树一样，我们同理可以通过中序和后序还原二叉树。

 例：下图为一个表达式的语法树，该表达式的后缀形式为(50)。

 

A. x 5 y + * a / b - 　　B. x 5 y a b*+/-

C. -/ * x + 5 y a b 　　 D. x 5 * y + a/b-

只需要进行后序遍历即可，选A。

 例：某二叉树的先序遍历序列为 ABCDEF ，中序遍历序列为BADCFE ，则该二叉树的高度(即层数)为(59)。

(59)A.3　　B.4 　　C.5 　　D.6

解：根据先序遍历和中序遍历得此二叉树为：

 

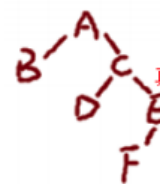
 层数是从1层开始，所以是4层。