归并排序（merge sort）

In computer science, merge sort (also commonly spelled mergesort) is an efficient, general-purpose, comparison-based sorting algorithm. Most implementations produce a stable sort, which means that the implementation preserves the input order of equal elements in the sorted output. Mergesort is a divide and conquer algorithm that was invented by John von Neumann in 1945.[1] A detailed description and analysis of bottom-up mergesort appeared in a report by Goldstine and Neumann as early as 1948.[2]

 

来自 <https://en.wikipedia.org/wiki/Merge_sort>

翻译如下：

在CS领域，归并排序（merge sort）是一个高效的、多用途的、基于比较的排序算法。它的大多数实现是稳定的。这意味着，在排序过程中，值相等的元素的相对顺序不会发生改变。归并排序是一种分治算法（divide and conquer algorithm），由约翰·冯·诺依曼在1945年发明。

 

归并排序的最差时间复杂度为O(n log n)。

归并操作：

归并操作（merge），也叫归并算法，指的是将两个已经排序的序列合并成一个序列的操作。归并排序算法依赖归并操作。

迭代法[编辑]

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置
3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
4. 重复步骤3直到某一指针到达序列尾
5. 将另一序列剩下的所有元素直接复制到合并序列尾

递归法[编辑]

原理如下（假设序列共有n个元素）：

1. 将序列每相邻两个数字进行归并操作，形成个序列，排序后每个序列包含两个元素

2. 将上述序列再次归并，形成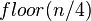个序列，每个序列包含四个元素

3. 重复步骤2，直到所有元素排序完毕

 

来自 <https://zh.wikipedia.org/wiki/%E5%BD%92%E5%B9%B6%E6%8E%92%E5%BA%8F>

 

package com.yan.algorithm;

import java.util.Arrays;
/**
 * merge sort java implementation.
 * @author Yan
 *
 */
public class MergeSort {
    private static int[] data = new int[] { 6, 5, 3, 1, 8, 7, 2, 4 };

    public MergeSort() {
    }

    public static void main(String[] args) {
        mergeSort(data);
        System.out.println(Arrays.toString(data));
    }

    public static void mergeSort(int[] data) {
        int[] temp = new int[data.length];
        mergeSort(data, temp, 0, data.length - 1);
    }

    public static void mergeSort(int[] data, int[] temp, int left, int right) {
        if (left < right) {
            int mid = (left + right) >> 1;
            // recursively divide the array to two parts by the median index.
            mergeSort(data, temp, left, mid);
            mergeSort(data, temp, mid + 1, right);
            // merge the divided two fragments to one sorted fragment.
            merge(data, temp, left, mid, right);
        }
    }

    public static void merge(int[] data, int[] temp, int left, int mid, int right) {
        // declare a indexPoint to step move in the right part;
        // for the left part the "left" can be used as a indexPoint.
        int rightPoint = mid + 1;
        // declare a indexPoint to step move in the temporary array.
        int tempPoint = left;
        // mark the whole length of the two parts, to control to write the
        // temporary array into the original array.
        int num = right - left + 1;
        /*
         * merge the two part array in sequence.
         */
        while (left <= mid && rightPoint <= right) {
            if (data[left] <= data[rightPoint]) {
                temp[tempPoint++] = data[left++];
            } else {
                temp[tempPoint++] = data[rightPoint++];
            }
        }
        /*
         * if the left part has rest, copy the left rest elements into the temp
         * array.
         */
        if (left <= mid) {
            for (int i = left; i <= mid; i++) {
                temp[tempPoint++] = data[i];
            }
        }
        /*
         * if the right part has rest, copy the right rest elements into the
         * temp array.
         */
        if (rightPoint <= right) {
            for (int i = rightPoint; i <= right; i++) {
                temp[tempPoint++] = data[i];
            }
        }
        /*
         * write the sorted temp array back to the original data array. num
         * controls the number to write.
         */

        for (int i = 0; i < num; i++, right--) {
            data[right] = temp[right];
        }
    }

}