位置编码，对句子中词汇位置进行编码

 

为什么需要位置编码

在任何语言中，词语的位置和顺序对句子的意思都至关重要；

在 RNN 中，以序列的模式逐个处理句子中的词语，这种网络结构天然保存了词语的顺序信息；

但在 词嵌入 时，单词并不是以 词在 句子中的顺序进行 embedding 的，而是很随意的把所有词进行 embedding，而不考虑词的顺序；

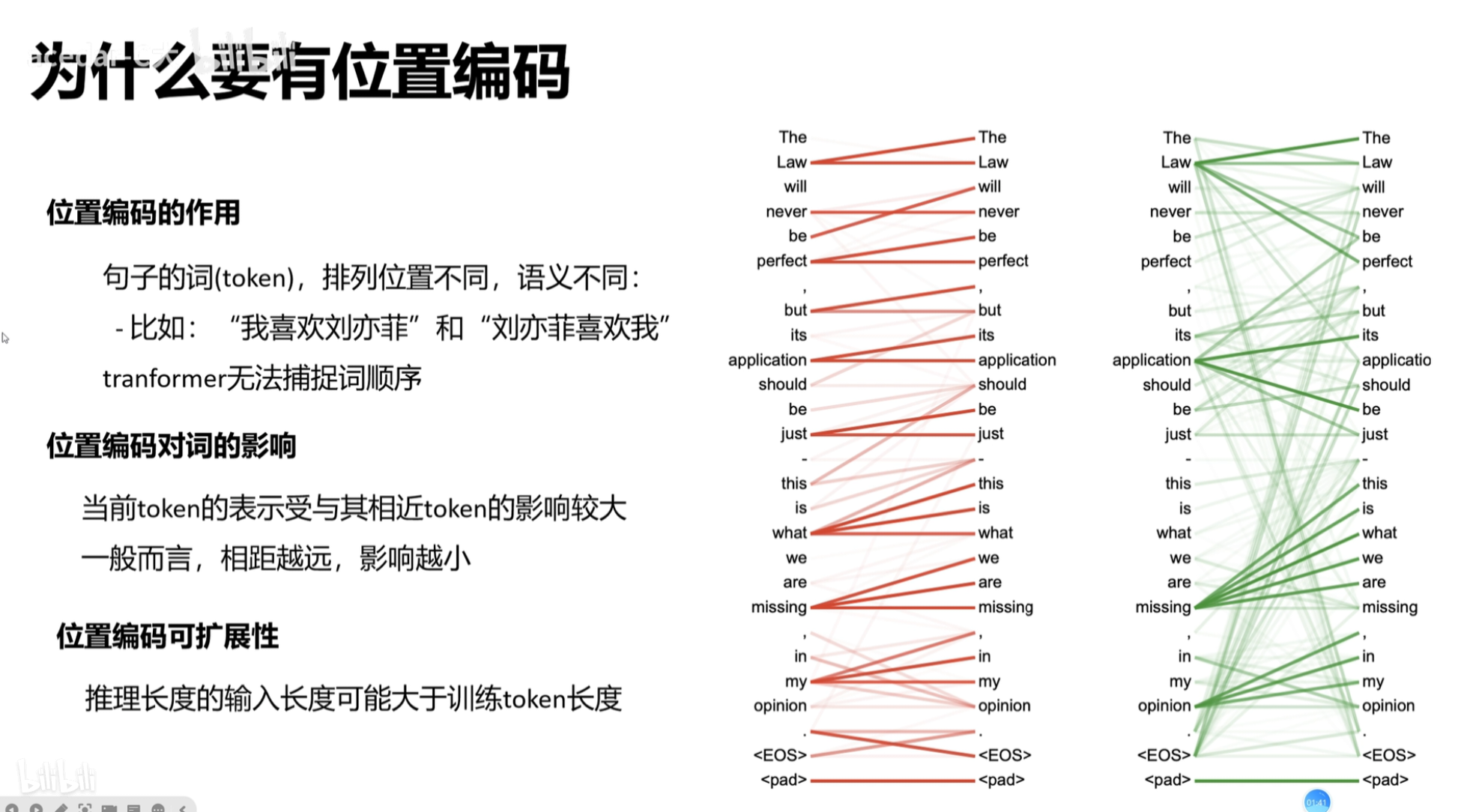
如果不增加对位置信息的编码，则对于模型来说，乱序的词汇和正序的词汇没有分别。也即“今天 天气 真 好”和 "天气 真 今天 好 "没有区别。

transformer 的输入其实就是 词向量，而词向量已经丧失了词的位置和顺序关系，故需加入该信息，就是 Position Encoding;

一句话概括，Positional Encoding就是句子中词语相对位置的编码，让Transformer保留词语的位置信息。

 

Position Encoding 类型分析

要加入 词语 在 句子 中的 位置信息，有几种思路：

1. 给每个词语添加一个线性增长的时间戳：即每个词一个下标，如 从0开始，第一个词0，第二个词1，依次...，第N个词N，

----但是 每个句子长度不一，如果句子很长，N会很大，Position Encoding 和 Word Embedding 合并后，模型可能更多关注 Position Encoding（大），这肯定是有问题的；

2. 归一化的时间戳：既然长句子N很大，那归一化处理，把 encoding 限制在 [0 1]之间呢？

----这会造成不同长度的句子，相邻词之间的步长不一致，使得 encoding 无法正确描述 词与词 之间的关系；

我们关注的位置信息，最核心的就是相对次序关系，尤其是上下文中的次序关系。也就是关注一个token与另一个token距离的相对位置（距离差几个token）。应该让位置1和位置2的距离比位置3和位置10的距离更近，位置1和位置2与位置3和位置4都只相差1

 

故理想 position encoding 应具备以下条件

对于每个位置（时间节点）的词语，都具备独一无二的编码

编码有一定的值域范围，避免比 word embedding 大很多，使得模型倾向于 position

需要体现一定的相对次序关系，并且在一定范围内的编码差异不应该依赖于文本长度，具有一定translation invariant平移不变性

 

transformer 中的 位置编码

transformer中的位置编码叫 正弦编码，公式如下

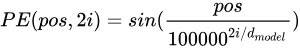
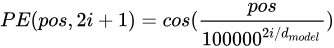
pos是词的输入序列中的位置，dmodel是维度，i表述编码中的位置，偶数位置用正弦，奇数位置用余弦；

举例说明，pos=3,d(model)=128，位置编码如下

[sin(3/10000^{0/128}), cos(3/10000^{0/128}), sin(3/10000^{2/128}), sin(3/10000^{2/128}),...]

 

位置编码PE和词向量的维度需要保持一致，才能相加。

 

频率递减

Sinusoidal位置编码的每个分量都是正弦或余弦函数，所以每个分量的数值都具有周期性。

并且越靠后的分量，波长越长，频率越低。

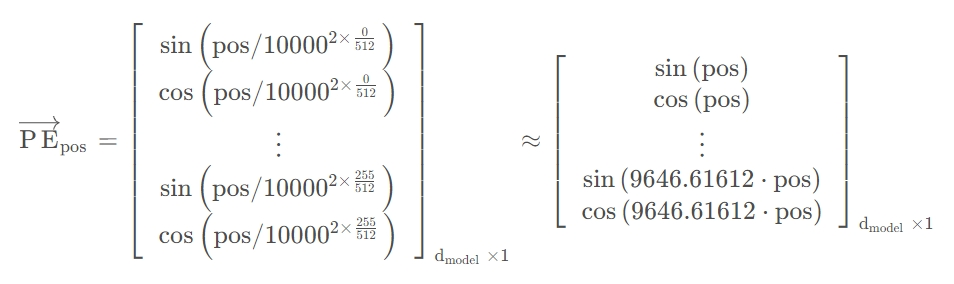
从每行来看，pos取值为1，2，3...，如果把1/100002i/d看作t，sin(t)，sin(2t)，sin(3t)...，就是sin(wt)，每行就是某频率的正(余)弦函数；

从每列来看，pos取值相同，1/100002i/d越来越小，故在列方向上，w越来越小，频率越来越低

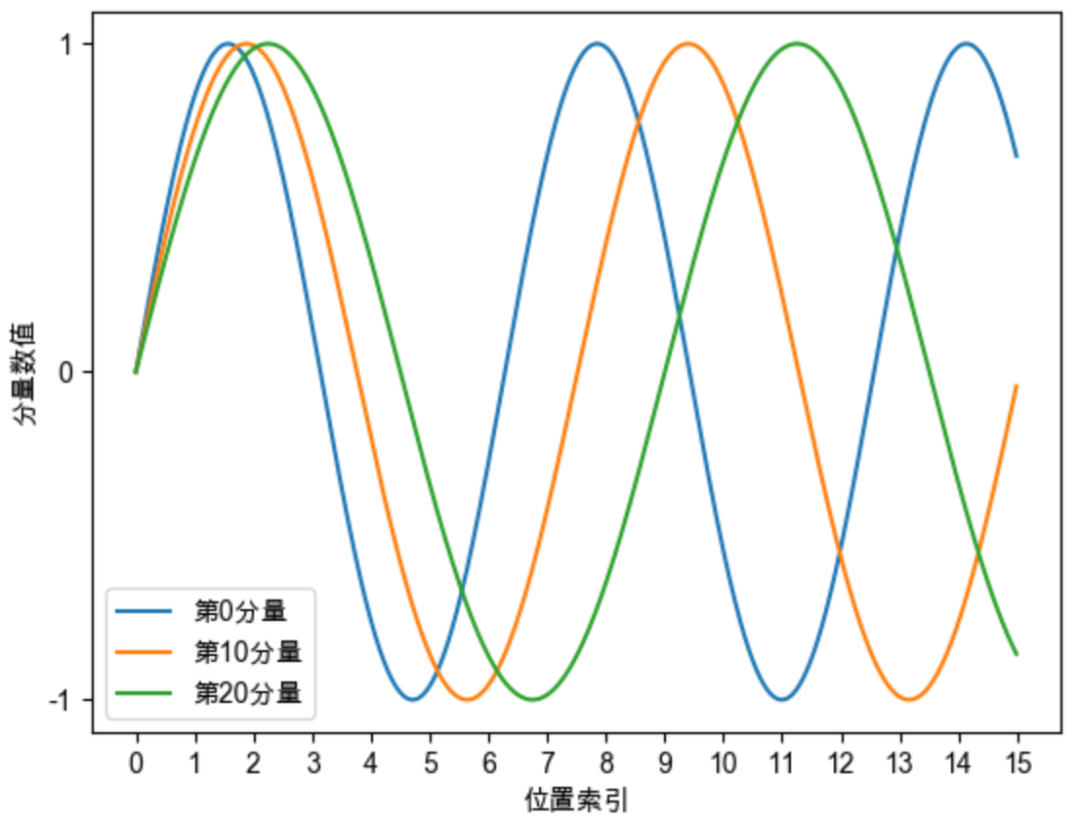
这是一个非常重要的性质，基于RoPE的大模型的长度外推工作，与该性质有着千丝万缕的关联，后续我们会进行分享。

 

远程衰减 

Sinusoidal位置编码还具有远程衰减的性质，具体表现为：对于两个相同的词向量，如果它们之间的距离越近，则他们的内积分数越高，反之则越低。如下图所示，我们随机初始化两个向量q和k，将q固定在位置0上，k的位置从0开始逐步变大，依次计算q和k之间的内积。我们发现随着q和k的相对距离的增加，它们之间的内积分数震荡衰减。

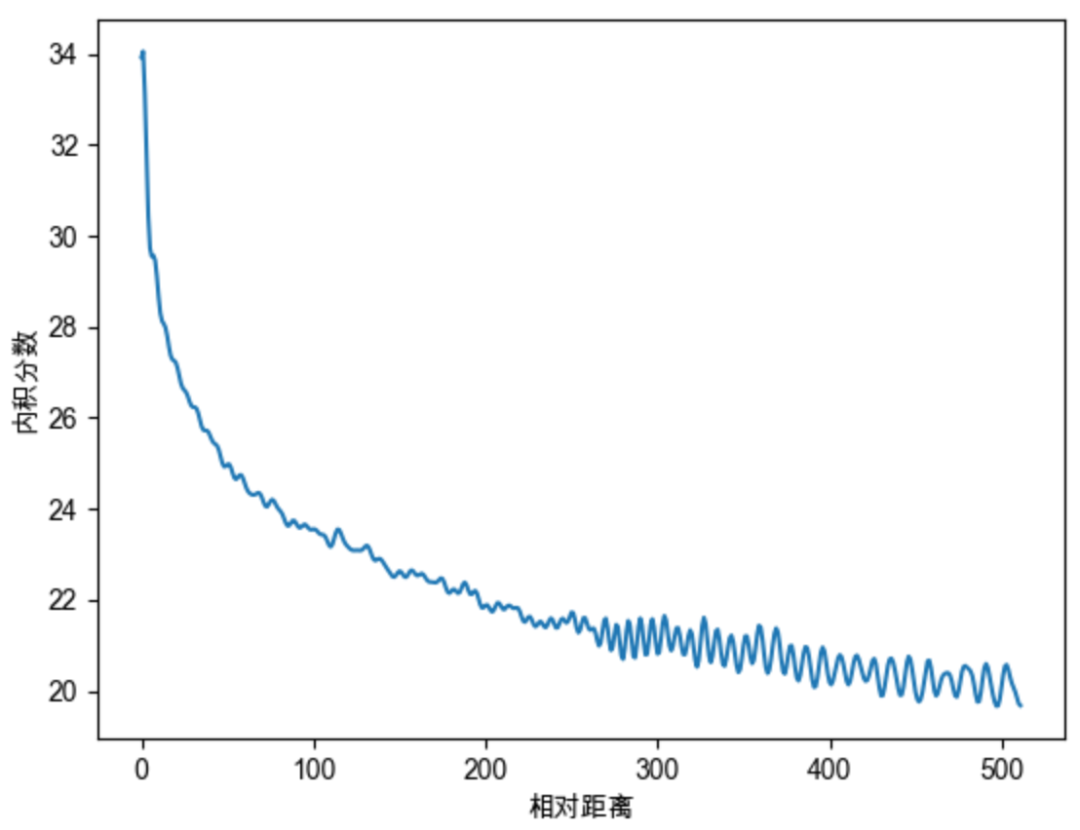
因为Sinusoidal位置编码中的正弦余弦函数具备周期性，并且具备远程衰减的特性，所以理论上也具备一定长度外推的能力。

 

代码实现

只是实现了上面的公式，参考一下就行了

class PositionalEncoding(nn.Module):

    def __init__(self, d_model, max_len=5000):
        super(PositionalEncoding, self).__init__()       
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0).transpose(0, 1)
        #pe.requires_grad = False
        self.register_buffer('pe', pe)

    def forward(self, x):
        return x + self.pe[:x.size(0), :]
View Code

 

为什么公式可以体现出相对次序关系

第二篇参考资料简单解释了一下，我觉得没有证明为什么，只是形象比喻了一下，仅供参考吧

 　　　　　　　　　　　　　　128维位置编码2D示意图

 

看看下面的解释吧

位置编码类型

绝对位置编码：每个位置都进行了位置建模

相对位置编码：对位置的相对关系 k-j 进行编码，自然语言一般更依赖于相对位置

正弦编码属于 绝对位置编码，但能在一定程度上体现 相对位置编码 的能力

和差化积

由于三角函数的性质，表明位置a+b的向量可以表示成位置a和位置b的向量组合，这提供了表达相对位置信息的可能性。 

 

 

 

参考资料：

https://blog.csdn.net/qq_40744423/article/details/121930739　　详解Transformer中的Positional Encoding   推导了相对次序关系

https://zhuanlan.zhihu.com/p/338592312　　一文教你彻底理解Transformer中Positional Encoding

https://www.jianshu.com/p/251a0530bc0e　　Transformer中的positional encoding