自注意力与注意力机制的区别在于，自注意力不依赖于外部信息，其 q k v 均来自内部，或者说来自输入 x，
就像我们看到一张狗的照片，尽管照片中有其他物体，但人类能自动聚焦到狗的身上，
自注意力更擅长捕捉内部相关性，能更好解决长距离依赖问题。
原理
首先，初始化 Embedding 和 Wq，Wk，Wv
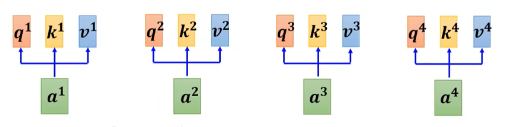
接着执行下面这张图
补充：softmax为什么要除以根号d
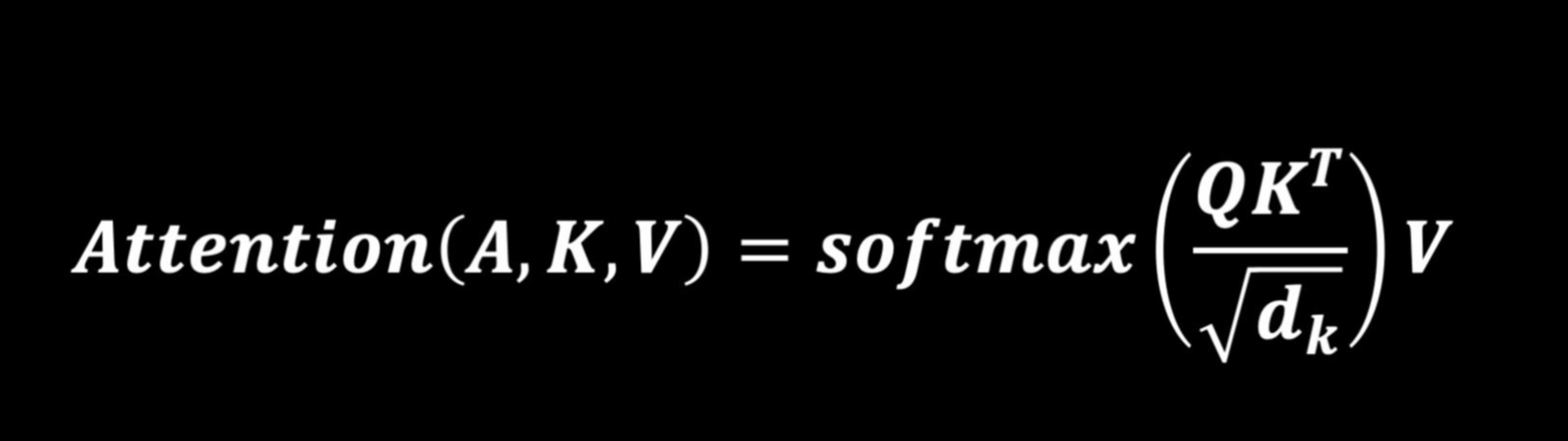
1.避免 向量维度的影响
2.由于指数的原因，也是 除以 根号dk 也是防止 在 score 差别不大时，softmax 算出来的概率差别很大，导致某些信息被遗漏
如 socre 60 40，softmax 0.9， 0.1，我没细算，理解意思即可
np.exp(14)/(np.exp(14)+np.exp(12)) = 0.88
3.由于指数的原因，ex很大，softmax 梯度很小，容易梯度消失
4.为了梯度的稳定，使用了score归一化，即除以 根号dk，【dk一般采用上文提到的矩阵的第一个维度的开方即64的开方8，当然也可以选择其他的值，但效果可能会差一点】
方差为1的分布更容易收敛
下图代表两个句子中it与上下文单词的关系热点图，很容易看出来第一个图片中的it与animal关系很强，第二个图it与street关系很强。
这个结果说明注意力机制是可以很好地学习到上下文的语言信息。
代码
看代码加深理解
import torch import torch.nn as nn import torch.nn.functional as F class Attention_Layer(nn.Module): def __init__(self, input_size, hidden_dim): super(Attention_Layer, self).__init__() self.hidden_dim = hidden_dim # 下面使用nn的Linear层来定义Q，K，V矩阵 self.Q_linear = nn.Linear(input_size, hidden_dim, bias=False) self.K_linear = nn.Linear(input_size, hidden_dim, bias=False) self.V_linear = nn.Linear(input_size, hidden_dim, bias=False) def forward(self, inputs, lens): # 一句话10个词 size = inputs.size() # [3, 10, 128] [b, maxlen, embed] # 计算生成QKV矩阵;Q=xWq Q = self.Q_linear(inputs) # [3, 10, 64] K = self.K_linear(inputs).permute(0, 2, 1) # 先进行一次转置 [3, 64, 10] V = self.V_linear(inputs) # [3, 10, 64] # xWq --> socre --> softmax --> wXnew score = torch.matmul(Q, K) # [3, 10, 10] 每个词和其他词的相似度 score = F.softmax(score, dim=2) # [3, 10, 10] # V [3, 10, 64]; # [10, "10(w)] * [10", 64] 中间两个10抵消，故第一个10应该是个weight，故上面是在dim2上softmax out = torch.matmul(score, V) # [3, 10, 64] # input --> out; old embedding --> new embedding return out if __name__ == '__main__': inputs = torch.rand(3, 10, 128) # 这里假设是RNN的输出，维度分别是[batch_size, max_len, w] att_L = Attention_Layer(128, 64) # w hidden_size lens = [7, 10, 4] # 一个batch文本的真实长度 att_out = att_L(inputs, lens) # 开始计算
注意绿色 代表权重，softmax * V 是要消掉权重，这决定了 两个矩阵 如何相乘，再看看下面的代码，对比一下
class selfattention(nn.Module): def __init__(self, in_channels): super().__init__() self.in_channels = in_channels # 像素点注意力 self.query = nn.Conv2d(in_channels, in_channels // 8, kernel_size=1, stride=1) self.key = nn.Conv2d(in_channels, in_channels // 8, kernel_size=1, stride=1) self.value = nn.Conv2d(in_channels, in_channels, kernel_size=1, stride=1) self.gamma = nn.Parameter(torch.zeros(1)) # gamma为一个衰减参数，由torch.zero生成，nn.Parameter的作用是将其转化成为可以训练的参数. self.softmax = nn.Softmax(dim=-1) def forward(self, input): batch_size, channels, height, width = input.shape # [3, 16, 12, 15] # input: B, C, H, W -> q: B, H * W, C // 8 q = self.query(input).view(batch_size, -1, height * width).permute(0, 2, 1) # [3, 180, 2] # input: B, C, H, W -> k: B, C // 8, H * W k = self.key(input).view(batch_size, -1, height * width) # [3, 2, 180] # input: B, C, H, W -> v: B, C, H * W v = self.value(input).view(batch_size, -1, height * width) # [3, 16, 180] # q: B, H * W, C // 8 x k: B, C // 8, H * W -> attn_matrix: B, H * W, H * W # 每个像素间的相关性 [3, 180, 180] attn_matrix = torch.bmm(q, k) # torch.bmm进行tensor矩阵乘法,q与k相乘得到的值为attn_matrix. attn_matrix = self.softmax(attn_matrix) # 经过一个softmax进行缩放权重大小. # [3, 16, 180] * [3, 180(w), 180] = [3, 16, 180] out = torch.bmm(v, attn_matrix.permute(0, 2, 1)) # tensor.permute将矩阵的指定维进行换位.这里将1于2进行换位。 out = out.view(*input.shape) # [3, 16, 12, 15] return self.gamma * out + input if __name__ == '__main__': inputs = torch.rand(3, 16, 12, 15) # [b c w h] att_L = selfattention(16) # c att_out = att_L(inputs)
1.上个代码是 softmax * v，这里 v * softmax，由于设定了 softmax 最后一维是 weight，故 这里 需要 把 最后一维的 weight 换到 倒数第二维，才能消掉weight
2. 本代码针对每个像素 添加了 注意力
再看几幅图吧，出自 第3篇资料
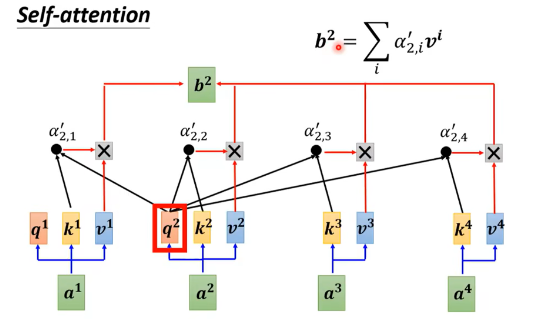
参考资料：
https://zhuanlan.zhihu.com/p/265108616 Attention注意力机制与self-attention自注意力机制 - 知乎 (zhihu.com)
https://blog.csdn.net/qq_41103479/article/details/119425133 自注意力机制（self-attention）的理解与pytorch实现
https://mp.weixin.qq.com/s/Ai1x4CT2X0mRoTatzStjKg 注意力机制系列2--self-attention的计算方式
https://mp.weixin.qq.com/s/U9SjIXLF-LLC_qhF0pOZXw 自注意力（Self-attention）清晰解释
