OpenCV4【15】-霍夫变换

在图像处理中，霍夫变换可以用来检测 各种形状，如 直线、圆、椭圆 等

 

霍夫空间

在笛卡尔坐标系下，一条直线可以表示为 y=kx+b，两点可以确定一条直线；

如果把表达式改为  b=-kx+y，则转换到了 霍夫空间，该空间 横坐标是 k，纵坐标是 b，可以看到 一组 (k，b) 就可以确定一条直线；

即 霍夫空间的一个点 就可以确定 笛卡尔坐标系下 的一条直线，

反过来也成立，霍夫空间的一条直线 对应 笛卡尔坐标系下 的一个点；

 

如果 霍夫空间的两条直线 相交于 霍夫空间的某个点 X，X 对应了 笛卡尔坐标系下的一条直线 L，霍夫空间的两条直线 又对应了笛卡尔坐标系下的两个点 A B，则 L 经过 A B

 

有点绕，看图

笛卡尔坐标系 转换到 霍夫空间后，如果 存在如下关系，则说明 笛卡尔坐标系下的点 在 一条直线上 

 

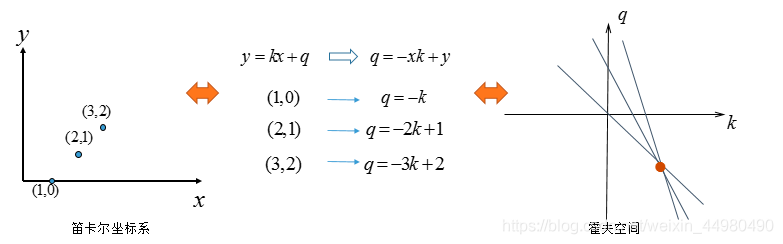
以上用笛卡尔坐标系讲了半天，只是为了方便理解，实际在 霍夫变换 中用的不是 笛卡尔，因为 当直线 垂直于 坐标轴时，k 等于 无穷大；

 

极坐标

霍夫变换中 采用的是 极坐标系；

极坐标系下的r=xcos(theta)+ysin(theta)。即可用（r,theta）来表示一条直线。其中 r 为该直线到原点的距离，theta 为该直线的垂线与x轴的夹角。如下图所示

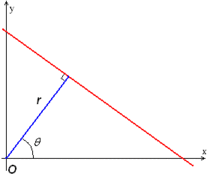
很多资料用 ρ 代表 r

 

极坐标下 与 霍夫空间对应关系类似  笛卡尔坐标

 

 

霍夫线检测

在实际应用中，我们初始化一个矩阵，

行代表 ρ ，通常以像素为单位，一般以 1 个像素为单位，最大值为 对角线的 长度；

列代表 θ，通常以弧度为单位，一般以 1弧度为单位，最大为 180；

霍夫检测 需要图像为 二值图（0， 255），然后检测 255 （白色点）所在位置（x，y）对应的 （ρ，θ）；　　　　【经测试，不一定是 255，其他也行，155都行，自己试试吧】

在 矩阵对应位置 计数 （+1）；

最后 取 矩阵中 大于 num（人工设定）的 （ρ，θ），其对应的 白色点（x，y）构成图像中的一条直线；

 

OpenCV 用法

两种方法

标准霍夫变换（多尺度霍夫变换）

def HoughLines(image, rho, theta, threshold, lines=None, srn=None, stn=None, min_theta=None, max_theta=None)

image：8-bit, single-channel binary source image，单通道 二值图

rho：以像素为单位的 step， 对应上面矩阵中的行

theta：以弧度为单位的 step，对应上面矩阵中的列

threshold：累计经过 （ρ，θ）的阈值，大于 阈值 认为是一条直线，对应上面的 num

return：返回的是一个包含 rho 和 theta 的数组，[rho,theta]

 

示例

import cv2 as cv
import numpy as np

# 构建测试图片
image = np.zeros((100, 100), dtype=np.uint8)    # 背景图
idx = np.arange(25, 75)                         # 25-74 序列
image[idx[::-1], idx] = 155                     # 对角线 \     注意这里不是 255，专门测试下
image[idx, idx] = 255                           # 对角线 /

# hough 线变换
lines = cv.HoughLines(image.astype(np.uint8), 1, np.pi/180, 10)
print(lines)

for line in lines:
    rho, theta = line[0]
    a = np.cos(theta)
    b = np.sin(theta)
    x0 = a * rho
    y0 = b * rho
    x1 = int(x0 + 50 * (-b))
    y1 = int(y0 + 50 * (a))
    x2 = int(x0 - 50 * (-b))
    y2 = int(y0 - 50 * (a))
    print(x1, y1, x2, y2)
    cv.line(image, (x1, y1), (x2, y2), (0, 0, 255), 2)

cv.imshow('hog', image)
cv.waitKey(0)

 

渐进式霍夫变换

def HoughLinesP(image, rho, theta, threshold, lines=None, minLineLength=None, maxLineGap=None)

参数同上

return:返回的是含有一条直线的起始点和终点坐标[x1,y1,x2,y2]

 

示例

import cv2 as cv
import numpy as np

src = cv.imread('imgs/55555.png')
gray = cv.cvtColor(src, cv.COLOR_BGR2GRAY)

# 应用直方图均衡化
dst = cv.equalizeHist(gray)

# 高斯滤波降噪
gaussian = cv.GaussianBlur(dst, (11, 11), 0)

# 利用Canny进行边缘检测
edges = cv.Canny(gaussian, 80, 180, apertureSize=3)

# 自动检测可能的直线，返回的是一条条线段
# 第二个参数为半径的步长，第三个参数为每次偏转的角度
lines = cv.HoughLinesP(edges, 1, np.pi/180, 80, minLineLength=37, maxLineGap=6)
print(type(lines))
for line in lines:
    x1, y1, x2, y2 = line[0]
    cv.line(src, (x1, y1), (x2, y2), (0, 0, 255), 2)

cv.imshow("line", src)
cv.waitKey(0)
cv.destroyAllWindows()

 

霍夫圆检测

1. 霍夫线检测输入为 二值图，霍夫圆检测输入可为 灰度图，不必为 二值图

2. 圆公式 (x-xc)^2 + (y-yc)^2 = r^2，故霍夫圆检测需确定 圆心 半径 3个参数，其他类似于霍夫线检测

3. 理论上圆检测比线更耗时，opencv采用了一种霍夫梯度法，优化了效率，感兴趣的可以研究下

def HoughCircles(image, method, dp, minDist, circles=None, param1=None, param2=None, minRadius=None, maxRadius=None)

image：8位 单通道 灰度图

method：使用的检测方法，opencv 中只有一种可以使用，即霍夫梯度法，cv2.HOUGH_GRADIENT

dp：累加面分辨率（大小） = 原始图像分辨率（大小） × 1/dp。默认 dp = 1 时，两者分辨率相同，应该类似于 霍夫线检测 中的 step

minDist：检测到的圆的圆心间的最小距离，如果小于该值，视为同一个圆

circles：输出参数格式，只有两种 (x, y, radius) or (x, y, radius, votes)

param1：Canny 边缘检测的高阈值，低阈值被自动置为高阈值的一半，默认为 100

param2：累加平面某点是否是圆心的判定阈值。它越大，能通过检测的圆就更接近完美的圆形，默认为 100，类似于 霍夫线检测 中的 num

minRadius：最小半径，默认 0，

maxRadius：最大半径，默认 0，最好规定 最小最大半径，不能盲目检测，否则浪费时间空间

 

示例代码

img = cv2.imread('imgs/3.png')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
gaussian = cv2.GaussianBlur(gray, (7, 7), 0)
edges = cv2.Canny(gaussian, 80, 180, apertureSize=3)

# 自动检测圆
circles1 = cv2.HoughCircles(edges, cv2.HOUGH_GRADIENT, 1, 1, param1=10, param2=10, minRadius=200, maxRadius=295)
print(np.shape(circles1))

circles = circles1[0, :, :]
circles = np.uint16(np.around(circles))
for i in circles[:]:
    cv2.circle(img, (i[0], i[1]), i[2], (0, 255, 0), 3)
    #cv2.circle(img, (i[0], i[1]), 2, (255, 0, 255), 10)

cv2.imshow('img', img)
cv2.waitKey(0)
cv2.destroyAllWindows()

 

 

 

 

参考资料： 

https://blog.csdn.net/weixin_44980490/article/details/107507219　　　　霍夫变换 原理讲的比较清楚，结合我的文章和这篇资料，你会懂的

https://www.jb51.net/article/132762.htm　　　　　　　　　　　　极坐标 讲的比较好

http://www.woshicver.com/FifthSection/4_13_%E9%9C%8D%E5%A4%AB%E7%BA%BF%E5%8F%98%E6%8D%A2/　　　　还不懂的话 看看这篇

https://blog.csdn.net/qq_45769063/article/details/108556794　　　　有原理，有 参数解释，参数解释比较详细

https://blog.csdn.net/on2way/article/details/47028969

https://blog.csdn.net/wsp_1138886114/article/details/82936218

https://www.jianshu.com/p/70618e629f17

https://www.cnblogs.com/bjxqmy/p/12333022.html　　　　霍夫圆检测 参数解释 c++