EMD EEMD
EMD,经验模态分解,是一种信号分解的技术;
它提出了一个概念叫 基本模态分量 IMF,
EMD 用于处理非平稳信号,可用于任意数据,基于数据本身进行分解;
EMD 把一个信号分解成 多个 IMF,每个 IMF 具有线性和非线性的特点,还有一个 信号残余分量,常常代表信号的直流分量或者信号的趋势;
EMD 分解得到的 IMF,频率逐渐降低,尺度各不相同;
EMD 分解得到的前几个模态分量,通常集中了原始信号中最显著、最重要的信息;
模态混合 缺陷
EMD 分解容易造成 模态混合,表现为下列现象之一:
1. 在同一个 IMF 中,尺度分布范围很宽却又各不相同的信号;

2. 在不同 IMF 中,存在尺度相近的信号;
模态混合使得 IMF 失去单一特征尺度,形成尺度混杂的震荡,失去原有的物理意义
EEMD,集合经验模态分解,解决了 EMD 模态混合的现象
特点
傅里叶变换 的 基波 为 正弦波,如果原始信号波形很复杂,信号分解 计算量会很大,用 无穷多的 正弦波 才能 逼近 这个 波形;
小波变换 的 基波 为 某些固定波形,不同的 基波 对信号处理影响很大,一旦选定,无法更换,即使小波基在全局最佳,在某些局部却不一定;
经验模态分解的特点在于 自适应 的基函数(基波),使得它 可以处理 任意 信号;
基本用法
安装:pip install EMD-signal
文档:https://pyemd.readthedocs.io/en/latest/
Python EMD 用法

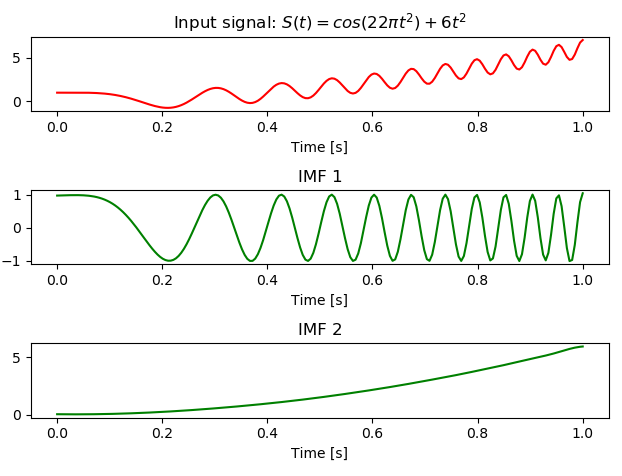
##### 基本用法 import numpy as np from PyEMD import EMD import pylab as plt s = np.random.random(100) emd = EMD() IMFs = emd.emd(s) ##### 示例 # Define signal t = np.linspace(0, 1, 200) s = np.cos(11*2*np.pi*t*t) + 6*t*t # Execute EMD on signal IMF = EMD().emd(s,t) N = IMF.shape[0]+1 # Plot results plt.subplot(N,1,1) plt.plot(t, s, 'r') plt.title("Input signal: $S(t)=cos(22\pi t^2) + 6t^2$") plt.xlabel("Time [s]") for n, imf in enumerate(IMF): plt.subplot(N,1,n+2) plt.plot(t, imf, 'g') plt.title("IMF "+str(n+1)) plt.xlabel("Time [s]") plt.tight_layout() plt.savefig('simple_example') plt.show()
Python EEMD 用法
def eemd(self, S, T=None, max_imf=-1)
S:一维信号
T:时间,相当于 x,如果没有 时间,就用 None
max_imf:分解成多少个 基本模态分量,注意 还有一个 残余分量,也就是 max_imf = 2 的话,有生成 3 个 imf
示例

from PyEMD import EEMD import numpy as np import pylab as plt def main(): # Define signal t = np.linspace(0, 1, 200) sin = lambda x,p: np.sin(2*np.pi*x*t+p) S = 3*sin(18,0.2)*(t-0.2)**2 S += 5*sin(11,2.7) S += 3*sin(14,1.6) S += 1*np.sin(4*2*np.pi*(t-0.8)**2) S += t**2.1 -t # Assign EEMD to `eemd` variable eemd = EEMD() # Say we want detect extrema using parabolic method # emd = eemd.EMD # emd.extrema_detection="parabol" # eemd.trials = 50 # eemd.noise_seed(12345) # Execute EEMD on S eIMFs = eemd.eemd(S, t, -1) nIMFs = eIMFs.shape[0] # Plot results plt.figure(figsize=(12,9)) plt.subplot(nIMFs+1, 1, 1) plt.plot(t, S, 'r') for n in range(nIMFs): plt.subplot(nIMFs+1, 1, n+2) plt.plot(t, eIMFs[n], 'g') plt.ylabel("eIMF %i" %(n+1)) plt.locator_params(axis='y', nbins=5) plt.xlabel("Time [s]") plt.tight_layout() plt.savefig('eemd_example', dpi=120) plt.show() if __name__ == '__main__': main()
注意
1. 使用时 数据 是 浮点数;
2. eemd 必须 使用 if __name__ == '__main__' 运行,不知道为什么
高阶应用
经验模态分解 认为 任何 一个复杂信号 都可以分解成若干个 基本模态分量 imf;
这些基本模态分量相加 也可以 大致 重构 原始信号;
去燥 与 重构
我们把 imf 进行 频谱分析后,频率最高的就是 噪声,把 这个 imf 以外的 imf 相加,就可以达到去燥效果;
import numpy as np import matplotlib.pylab as plt from PyEMD.EEMD import EEMD from scipy.fft import fft if __name__ == '__main__': t = np.linspace(0, 100, num=100) S = 3*np.sin(2*np.pi*10*t) # 10HZ S += 5*np.sin(2*np.pi*4*t) # 4HZ S += np.random.randn(100, ) # 白噪声 eemd = EEMD() imfs = eemd.eemd(S, T=t, max_imf=-1) print(imfs.shape) rows = 2 * imfs.shape[0] + 1 ### 信号重构 plt.subplot(311); plt.title('original') plt.plot(S) plt.subplot(312); plt.title('sum all imfs') sum_imf0 = np.sum(imfs, axis=0) plt.plot(sum_imf0) plt.subplot(313); plt.title('sum no noise imfs') sum_imf1 = np.sum(imfs[1:, :], axis=0) plt.plot(sum_imf1) plt.show()

可以看到 第 2 个图 和 原始信号 基本一致;
第 3 个图 明显 光滑了,去燥的结果;
特征提取
这些 imf 具有不同的特征尺度,比 原始信号更有规律性;
我们可以对 这些 imf 进行特征提取,如 幅值、频谱分析、样本熵计算 等;
接上面的代码,进行频谱分析;
plt.subplot(rows, 1, 1) plt.plot(S) for i in range(imfs.shape[0]): plt.subplot(rows, 1, i*2+2) plt.plot(imfs[i]) # imf 分量 y_fft = np.abs(fft(imfs[i])) # 傅里叶变换进行频谱分析 plt.subplot(rows, 1, i * 2 + 3) plt.plot(y_fft, 'r') plt.show()
输出:第一个图是原始信号,后面 的 依次为 imf 分量 和 这个 imf 对应的 频谱(红色)

第一个 imf 分量 就是 白噪声,高频;
第二个 imf 分量 为 10HZ 的正弦波,频谱图 在 10HZ 处 凸起;
第三个 imf 分量 为 4HZ 的正弦波;
其他应用
残差的应用

方法融合
EMD 可能与其他方法进行融合,比如 先进行 去燥,再 EMD 分解,或者 先 小波分解降噪,再 EMD 分解
相关论文


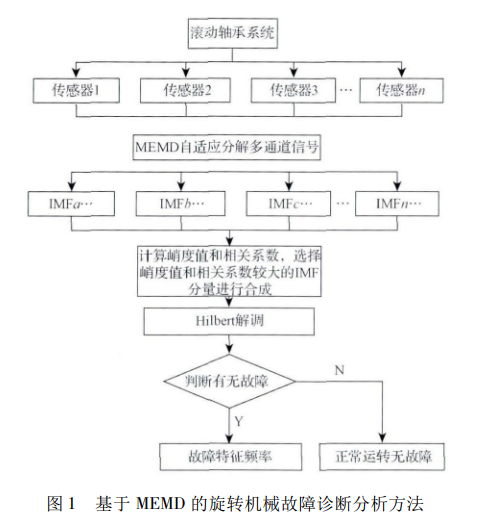
参考资料:
https://www.cnblogs.com/RoseVorchid/p/12030980.html EEMD算法python实现,原理讲得不咋地
http://www.360doc.com/content/19/0806/12/41357686_853284987.shtml# EEMD 原理
https://www.cnblogs.com/mikawong/p/7682467.html 记录了 PyEMD 的一些资源链接
《Adaboost_SVM集成模型的滚动轴承早期故障诊断》 电子书
https://zhuanlan.zhihu.com/p/40005057 这篇文章能让你明白经验模态分解(EMD)——基础理论篇



