高斯混合模型
混合模型，顾名思义就是几个概率分布密度混合在一起，而高斯混合模型是最常见的混合模型；
GMM，全称 Gaussian Mixture Model，中文名高斯混合模型，也就是由多个高斯分布混合起来的模型；
概率密度函数为
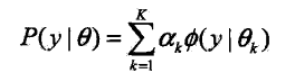
K 表示高斯分布的个数，αk 表示每个高斯分布的系数，αk>0，并且 Σαk=1，
Ø(y|θk) 表示每个高斯分布，θk 表示每个高斯分布的参数，θk=(uk，σk2)；
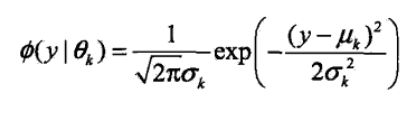
举个例子
男人和女人的身高都服从各自的高斯分布，把男人女人混在一起，那他们的身高就服从高斯混合分布；
高斯混合模型就是用混合在一起的身高数据，估计男人和女人各自的高斯分布
小结
GMM 实际上分为两步，第一步是选择一个高斯分布，如男人数据集，这里涉及取到某个分布的概率，αk，
然后从该分布中取一个样本，等同于普通高斯分布
GMM 常用于聚类，也就是把每个概率密度分布聚为一类；如果概率密度分布为已知，那就变成参数估计问题
EM 解释 GMM
EM 的核心是 隐变量 和 似然函数
求导结果如下
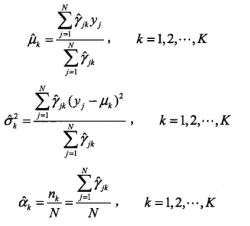
GMM 的 EM 算法
算法流程
Python 实现 GMM
import numpy as np import matplotlib.pyplot as plt from matplotlib.patches import Ellipse from scipy.stats import multivariate_normal plt.style.use('seaborn') # 生成数据 def generate_X(true_Mu, true_Var): ### 生成2000条二维模拟数据，其中400个样本来自N(μ1,var1) ,600个来自N(μ2,var2) ,1000个样本来自N(μ3,var3) # 第一簇的数据 num1, mu1, var1 = 400, true_Mu[0], true_Var[0] X1 = np.random.multivariate_normal(mu1, np.diag(var1), num1) # 第二簇的数据 num2, mu2, var2 = 600, true_Mu[1], true_Var[1] X2 = np.random.multivariate_normal(mu2, np.diag(var2), num2) # 第三簇的数据 num3, mu3, var3 = 1000, true_Mu[2], true_Var[2] X3 = np.random.multivariate_normal(mu3, np.diag(var3), num3) # 合并在一起 X = np.vstack((X1, X2, X3)) # 显示数据 plt.figure(figsize=(10, 8)) plt.axis([-10, 15, -5, 15]) plt.scatter(X1[:, 0], X1[:, 1], s=5) plt.scatter(X2[:, 0], X2[:, 1], s=5) plt.scatter(X3[:, 0], X3[:, 1], s=5) plt.show() return X # 更新W def update_W(X, Mu, Var, Pi): n_points, n_clusters = len(X), len(Pi) pdfs = np.zeros(((n_points, n_clusters))) for i in range(n_clusters): pdfs[:, i] = Pi[i] * multivariate_normal.pdf(X, Mu[i], np.diag(Var[i])) W = pdfs / pdfs.sum(axis=1).reshape(-1, 1) return W # 更新pi def update_Pi(W): Pi = W.sum(axis=0) / W.sum() return Pi # 计算log似然函数 def logLH(X, Pi, Mu, Var): # 仅计算损失，这步可有可无 n_points, n_clusters = len(X), len(Pi) pdfs = np.zeros(((n_points, n_clusters))) for i in range(n_clusters): pdfs[:, i] = Pi[i] * multivariate_normal.pdf(X, Mu[i], np.diag(Var[i])) return np.mean(np.log(pdfs.sum(axis=1))) # 画出聚类图像 def plot_clusters(X, Mu, Var, Mu_true=None, Var_true=None): colors = ['b', 'g', 'r'] n_clusters = len(Mu) plt.figure(figsize=(10, 8)) plt.axis([-10, 15, -5, 15]) plt.scatter(X[:, 0], X[:, 1], s=5) ax = plt.gca() for i in range(n_clusters): plot_args = {'fc': 'None', 'lw': 2, 'edgecolor': colors[i], 'ls': ':'} ellipse = Ellipse(Mu[i], 3 * Var[i][0], 3 * Var[i][1], **plot_args) ax.add_patch(ellipse) if (Mu_true is not None) & (Var_true is not None): for i in range(n_clusters): plot_args = {'fc': 'None', 'lw': 2, 'edgecolor': colors[i], 'alpha': 0.5} ellipse = Ellipse(Mu_true[i], 3 * Var_true[i][0], 3 * Var_true[i][1], **plot_args) ax.add_patch(ellipse) plt.show() # 更新Mu def update_Mu(X, W): n_clusters = W.shape[1] Mu = np.zeros((n_clusters, 2)) for i in range(n_clusters): Mu[i] = np.average(X, axis=0, weights=W[:, i]) return Mu # 更新Var def update_Var(X, Mu, W): n_clusters = W.shape[1] Var = np.zeros((n_clusters, 2)) for i in range(n_clusters): Var[i] = np.average((X - Mu[i]) ** 2, axis=0, weights=W[:, i]) return Var if __name__ == '__main__': # 生成数据 true_Mu = [[0.5, 0.5], [5.5, 2.5], [1, 7]] true_Var = [[1, 3], [2, 2], [6, 2]] X = generate_X(true_Mu, true_Var) # 初始化 n_clusters = 3 # 聚类个数 n_points = len(X) # 样本数 Mu = [[0, -1], [6, 0], [0, 9]] # 3 个期望 Var = [[1, 1], [1, 1], [1, 1]] # 3 个方差 Pi = [1 / n_clusters] * 3 W = np.ones((n_points, n_clusters)) / n_clusters # 隐变量，每个样本属于每个分布的概率 Pi = W.sum(axis=0) / W.sum() # 每个分布的比率 # 迭代 loglh = [] for i in range(5): plot_clusters(X, Mu, Var, true_Mu, true_Var) loglh.append(logLH(X, Pi, Mu, Var)) W = update_W(X, Mu, Var, Pi) Pi = update_Pi(W) Mu = update_Mu(X, W) print('log-likehood:%.3f'%loglh[-1]) Var = update_Var(X, Mu, W)
参考资料：
https://blog.csdn.net/jinping_shi/article/details/59613054
《统计学习方法》李航
