集成学习-Boosting 模型深度串讲

首先强调一下，这篇文章适合有很好的基础的人

 

梯度下降

这里不系统讲，只介绍相关的点，便于理解后文

 

先放一个很早以前写的 梯度下降 实现 logistic regression 的代码

def tiduxiajiang():
    """梯度下降算法"""
    alpha=0.000001       # 学习率的确定方法：看权值 w 的数量级，如该脚本中每次迭代w在 10的-5次方左右；线性回归脚本里w在0.07左右
    num=800               # 学习率对算法影响很大，先确定学习率，在确定迭代次数比较好

    w=np.zeros(x.shape[1])  # 初始权值
    sigmoid=lambda x,w:1/(1+np.exp(-np.dot(x,w.T)))   # sigmoid函数

    shoulian=[]
    for i in range(1,num+1):
        lose_function= (-np.dot(y,np.log10(sigmoid(x,w)))-np.dot(np.ones(x.shape[0])-y,np.log10(np.ones(x.shape[0])-sigmoid(x,w))))/x.shape[0] # 损失函数
        # 损失函数取负值， 是因为 本来是求最大值，取负之后是求最小，才能有梯度下降算法，否则要梯度上升
        # 损失函数/样本个数 是必须的 ，而且 这样求导后  grad 才会 也除以 样本个数
        shoulian.append(lose_function)

        grad=np.dot(1/x.shape[0]*x.T,np.dot(x,w.T)-y)
        w=w-np.dot(alpha,grad)
        print(w)
    return w,shoulian

 

我们只需要看一句  w=w-alpha*grad　　【学习率x梯度】

做如下理解

 

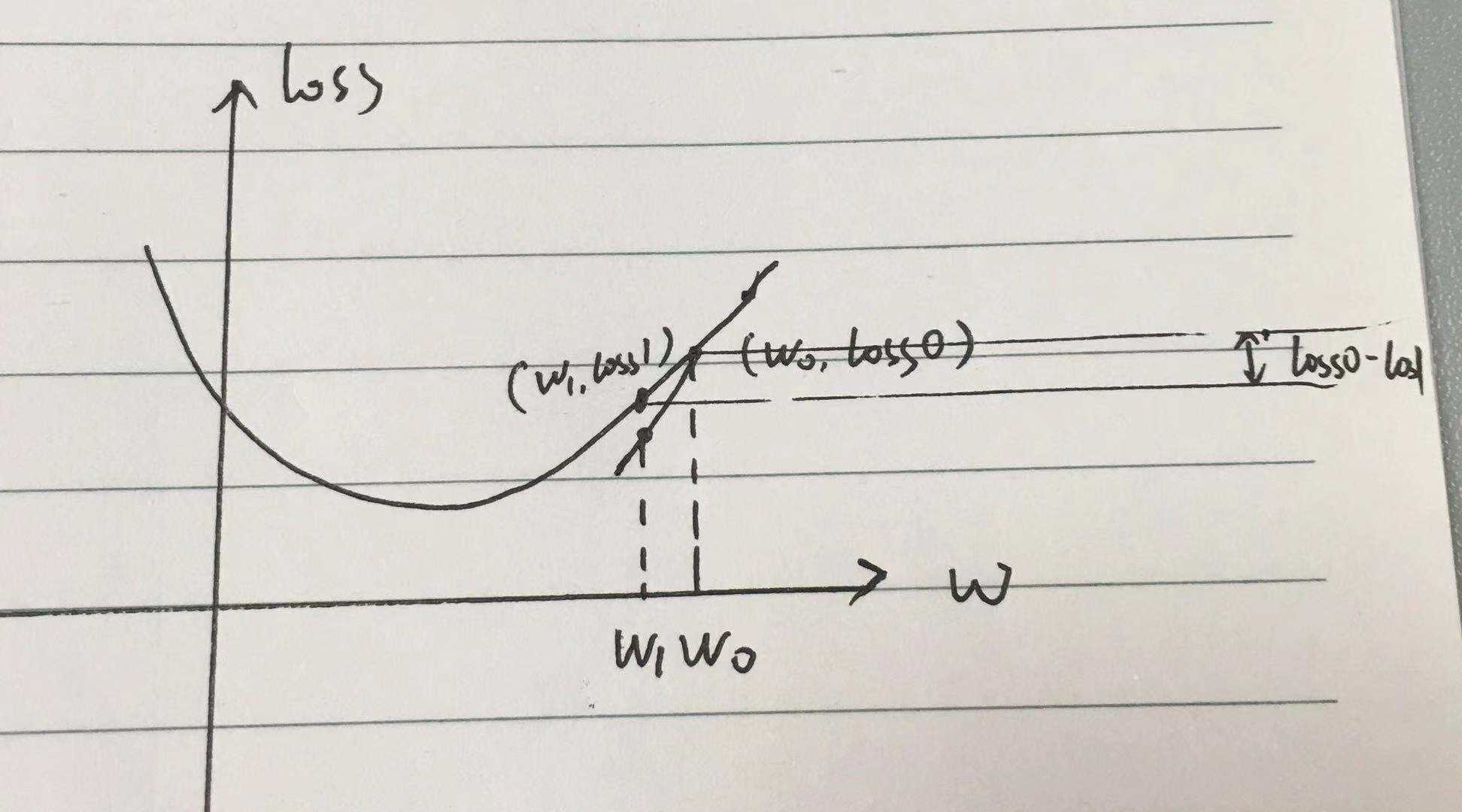
我们随机选了一个 w0，即初始化参数，w 是 loss function 中的自变量；

然后我们有了一个 loss0；然后我们沿着 loss 在 w0 处的 梯度grad 下降一个 学习率；

w0 走到了 w1，对应 loss 有个 loss1，loss1 要比 loss0 更小，我们减少的损失就是 loss0-loss1，也就是说我们逼近了 loss0-loss1 的距离；

如此往复，即可走到最低点，即 loss 最小值

 

加法模型 

我之前讲过，先看我的博客 加法模型与前向分步算法

 

 重点

是不是有点像梯度下降，对比一下

梯度下降是学习了一个 梯度，从而降低 loss，得到一个 新的 参数； 

加法模型是学习了一个 模型，从而降低 loss，得到一个新的 模型；

所以我们可以理解为 模型 是函数空间的 参数；

模型的方向就是 梯度的方向，也就是说 训练一个模型 是在 损失函数的负梯度上 学习了 一个参数，好好体会这句话；在加法模型中，训练一个模型 代表的是什么

 

据说加法模型是在 boosting 之后提出来解释 booting 的，所以 boosting 设计的初衷并没有加法模型，可能只是某些猜想

 

提升树

我之前讲过，先看我的博客 提升树

提升树是以 回归树或者分类树 为基学习器的，他的思路基本跟 加法模型一样

 

注意每次训练决策树时 数据集 是不同的，确切地说是 残差 是不同的 

 

分类提升树

回归很容易理解，那么分类问题呢？分类没有残差啊，貌似搞不清楚

其实分类问题的损失函数是指数函数

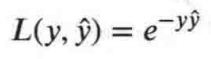
那如何使 loss 变小呢？貌似也不是很直观，这也是 提升树 的 缺点

 

在实际工作中，一般不会用到这个模型，甚至 python 都没有自带这个模型，

故这只是个基础模型，了解即可，由于它的缺点从而衍生了梯度提升树，而且在 梯度提升树中讲清楚了 分类问题 如何解决

 

梯度提升树 GDBT

我之前讲过，先看我的博客 回归梯度提升树 、分类与多分类梯度提升树

 

对提升树的改进

梯度提升树最大的改进就是用 负梯度替代了残差；

具体的说是 损失函数的负梯度在当前模型的值替代了残差

 

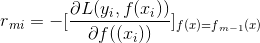
为什么负梯度可以替代残差？

我们从几个角度解释一下

1）如果损失函数是 mes

可以看到这种情况下，残差就是负梯度；所以 mes 是 负梯度代替残差的 特例

2）残差代表模型学习的目标，负梯度 = 负梯度x1 也是我们学习的目标，【1 我们可理解为学习率】

而且负梯度是 更直接的学习目标

3）从梯度的角度

之前我们讲到 训练一个模型 其实是在 loss 的负梯度上 学习一个参数，真的是啊

4） 损失函数 的一阶泰勒展开

个人比较喜欢这个解释；

这个解释也是 GDBT 和 XGBoost 的关键差异点，XGBoost 是泰勒二阶展开；

 

确切地说，负梯度不是代替了残差，负梯度是为了把损失函数扩展到其他函数 

 

GDBT 算法描述

根据 负梯度 算出所谓的“残差”之后，就可以拟合出一个模型 f(x)；

但是我们的 加法模型中是  F_m=F_m-1+βf_m(x)；

那 β 是多少？我们需要根据 最小化损失函数求得，并且把 βf_m(x) 作为 决策树的输出；

这个问题在 李航的 《统计学习方法》 中并没说的很明白，所以这里单独强调下

 

GDBT 的算法逻辑对于回归问题比较容易理解，也常用来解决回归问题，但是也能解决分类问题

 

GDBT 分类

这个问题其实我之前也讲过，不过今天讲到这里，我觉得可以稍微深入的讲一讲

 

首先，GDBT 是根据“残差”来拟合决策树，那么分类问题的 label 无法计算残差，解决这个问题的思路有以下几种：

1. 把类别标签转换成 概率，1 代表正例，概率为 1，-1或者0 代表负例，概率为 0，这样 基学习器可以选择回归树，把问题彻底转换成 回归问题

2. 还是上面的思路，只是基学习器还是分类树，只是输出为 概率值

3. 比较官方的作法，构造损失函数，使得负梯度变成连续值

　　// 损失函数有两种选择，一种是指数损失，一种是对数似然损失

　　// 如果是指数损失，退化为 Adaboost

 

对于 GDBT 二分类，采用类似于逻辑回归的对数似然损失

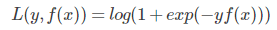 其中 y 为 {-1, 1}

其负梯度为

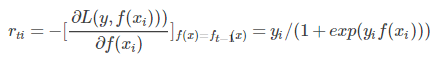
r 为连续值；

有了负梯度，就可以拟合决策树，注意这里拟合的仍然是回归树

 

然后根据 损失函数 线性搜索最佳的 β

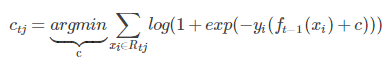
c = βf_t(x)

 

由于上式比较复杂，常用 近似值代替

 

然后迭代 F_t(x)；

然后重新计算 负梯度，迭代

 

在 SKlearn 中，就是采用这样方式，所以基学习器是个回归树

 

GDBT 也可以用于多分类，由于本篇幅会很大，这里不再赘述

 

xgboost

我之前讲过，先看我的博客 xgboost

 

xgboost 中对决策树进行了线性表达

f(x)=W[q(x)]；W 为每个叶节点的值，[W1,W2,W3...]，q 函数把 x 映射到某个叶节点，q(x) 为某个叶节点；

我们用 Ω(f(x)) 表示对这棵决策树的剪枝或者说正则 ；

 

首先我对网上的推导进行补充

 

 

下面的公式网上很多

 

这一系列变换最重要的是把 样本映射到每棵树的叶节点，从而把 nΣ 转换成了 TΣ

 

 

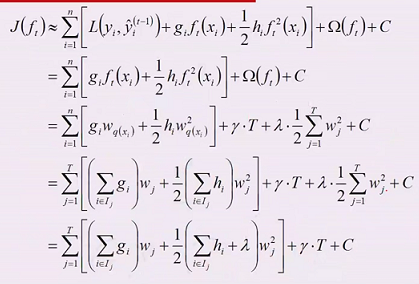
有了损失函数，要使得 loss 最小，一般是求导

 

我主要想说的

以上一系列公式貌似不难理解， 但是这一系列公式到底在干嘛？或者说想干嘛？

 

之前我们用 f(x) 表示决策树，然后推导了上面的一系列公式，最终得到了 min loss，也就是说我们如何得到 min loss，或者说 f(x) 是什么样时 loss 最小；

对了，上面一系列公式就是得到建树依据，类似于 信息增益、基尼系数 等指标；

其中的 G H 都是根据上一棵树得到；

 

有了建树原则，xgboost 就很好理解了，挨个建树就行了

 

adaboost

我之前讲过，先看我的博客 adaboost、adaboost 进阶

我觉得之前已经讲得很好了，不再赘述

 

这里只说明一个问题：adaboost 每次都训练一棵决策树，样本相同，特征相同，数据完全一致，那每次训练出来的决策树都一样，这能行吗？

这个问题你可能没思考过，数据确实是完全一致的，只是在评价分裂增益时，加入了样本权重，每轮权重都不同，所以同样的数据，得到的最佳分裂方式不同，所以得到的决策树是不同的

 

GDBT vs 提升树

提升树用残差来拟合决策树；

GDBT 用负梯度来拟合决策树；相当于提升树的泛化；

 

GDBT vs xgboost

1. 基学习器不同

GDBT 以 cart 树为基学习器；

xgboost 不仅可以是 cart 树，还可以是线性分类器，此时 xgboost 相当于 L1 L2 正则化的 logistic 回归 或者线性回归

2. 损失函数

GDBT 用 负梯度 代替残差，相当于 loss 的一阶泰勒展开；

xgboost 是 loss 的二阶泰勒展开，同时用到了 一阶导和二阶导，它支持自定义损失函数，只要一阶导和二阶导存在即可

3. 正则化

xgboost 对每棵决策树进行了正则化，而 GDBT 没有

4. learning rate：xgboost 带有 学习率，而 GDBT 可以没有

5. 并行化处理：在训练之前，预先对每个特征内部进行了排序找出候选切割点，然后保存为block结构，后面的迭代中重复地使用这个结构，大大减小计算量。在进行节点的分裂时，需要计算每个特征的增益，最终选增益最大的那个特征去做分裂，那么各个特

征的增益计算就可以开多线程进行，即在不同的特征属性上采用多线程并行方式寻找最佳分割点。

6. 列抽样（column subsampling）：xgboost借鉴了随机森林的做法，支持列抽样（即每次的输入特征不是全部特征），不仅能降低过拟合，还能减少计算，这也是xgboost异于传统gbdt的一个特性。

7. 忽略缺失值：在寻找splitpoint的时候，不会对该特征为missing的样本进行遍历统计，只对该列特征值为non-missing的样本上对应的特征值进行遍历，通过这个工程技巧来减少了为稀疏离散特征寻找splitpoint的时间开销

8. 指定缺失值的分隔方向：可以为缺失值或者指定的值指定分支的默认方向，为了保证完备性，会分别处理将missing该特征值的样本分配到左叶子结点和右叶子结点的两种情形，分到那个子节点带来的增益大，默认的方向就是哪个子节点，这能大大提升算法

的效率。

 

正则化

下面介绍几种正则化方法，仅介绍思路，每个方法可以适用于多个 boosting 模型

 

验证集 和 Early stopping

boosting 的主要参数是 叶节点个数 和 树的棵树；我们采用类似神经网络的 early stopping 策略

这种方式应该适合所有模型

 

early stopping

思想：一种迭代次数截断的方式来防止过拟合；也就是说在迭代未完成之前停止迭代

具体做法：

1. 划分训练集和验证集

2. 在训练集上进行训练，并在验证集上测试结果，一般是迭代 n 次，再进行测试

3. 如果发现验证集上效果变差，停止迭代，并将停止前的参数作为最终参数

 

好嘛，这不就是之前 深度强化学习 训练神经网络中的 fix target 吗，方法都是通用的

 

learning rate

这种方法有个官方的名字 Shrinkage，其实就是给 每步加上一个学习率

这种方法应该适合所有 boosting 模型

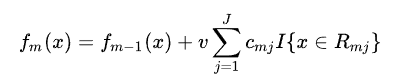
v 代表学习率，v 越小，树的棵树就越多

 

子采样

选择一部分样本来训练决策树，注意是无放回的，

样本数不要太少，也不要太多，一般选择 0.5-0.8 之间

这种方法应该适合所有 boosting 模型 

 

弱学习器的剪枝

很好理解，这种方法应该适合所有 boosting 模型 

 

 

 

参考资料：

 https://www.zhihu.com/question/63560633

https://zhuanlan.zhihu.com/p/59751960

https://www.cnblogs.com/gogoSandy/p/9315785.html

https://zhuanlan.zhihu.com/p/40096769