层次聚类

层次聚类也叫分层聚类，对数据进行逐层划分，最终形成树状的聚类结构。

数据集的划分可采用 “自顶向下” 的分割策略，也可采用 “自下而上” 的聚合策略。

 

聚合法-AGNES 算法

采用自下而上的聚合策略，初始每个样本为一个簇，然后每步找到距离最近的两个簇，并将它们融合，依次进行下去，直到所有样本在一个簇，或者到达指定类别数。

 

最短距离可以有多种定义

最小距离：两个簇中距离最近的样本之间的距离；用最小距离的层次聚类被称为 单链接

最大距离：两个簇中距离最远的样本之间的距离；用最大距离的层次聚类被称为 全链接

平均距离：两个簇中所有样本的距离的平均值；用平均距离的层次聚类被称为 均链接

 

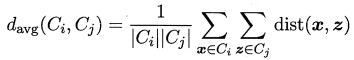
还有其他的距离计算方式，汇总如下

 

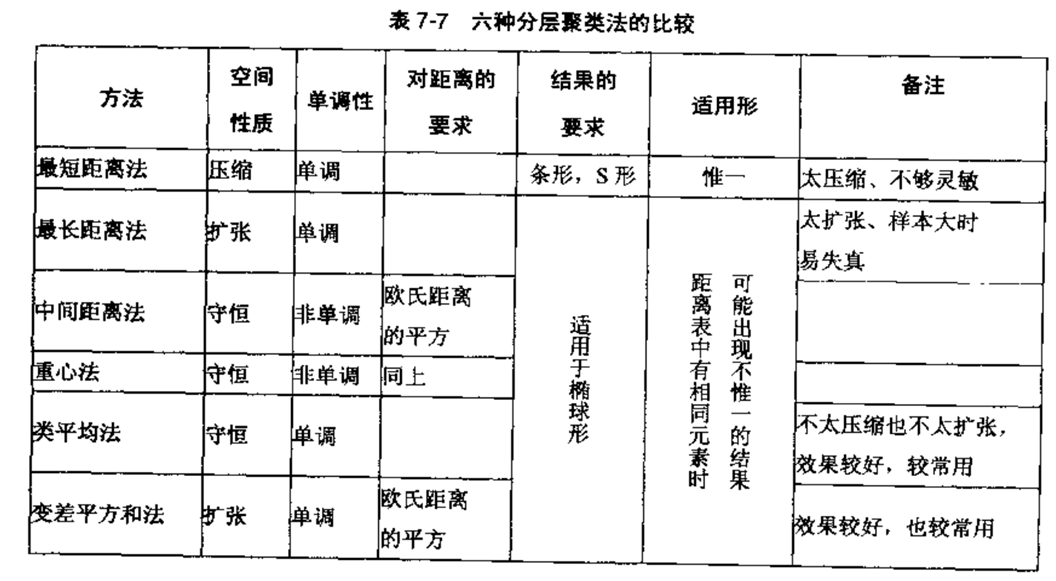
具体算法如下

 

分割法-DIANA 算法

采用自上而下的分割策略，初始所有样本为一个簇，每步将一个簇分成两个簇，使得这两个簇尽可能远离，递归的分割下去，直到每个样本为一个簇或者到达指定类别数。

 

道理非常简单，实现类似聚合法，具体不再赘述

 

层次聚类的优缺点

优点：距离定义简单；可以不预先设定类别数；可以发现类别间的层次关系；可以生成非球形簇

缺点：计算量大；对异常值敏感；很可能聚类成链状

 

python - API

方法1

from sklearn.cluster import AgglomerativeClustering
import numpy as np
X = np.array([[1, 2], [1, 4], [1, 0],
              [4, 2], [4, 4], [4, 0]])
clustering = AgglomerativeClustering().fit(X)

print clustering.labels_        # [1 1 1 0 0 0]

 

方法2

from scipy.cluster.hierarchy import dendrogram, linkage,fcluster
from matplotlib import pyplot as plt
X = [[i] for i in [2, 8, 0, 4, 1, 9, 9, 0]]
# X = [[1,2],[3,2],[4,4],[1,2],[1,3]]
Z = linkage(X, 'ward')
f = fcluster(Z,4,'distance')
fig = plt.figure(figsize=(5, 3))
dn = dendrogram(Z)
plt.show()

 

总结

层次聚类多用于 轨迹 或者 GPS 数据。

 

 

参考资料：

https://scikit-learn.org/stable/modules/generated/sklearn.cluster.AgglomerativeClustering.html　　sklearn 层次聚类

https://blog.csdn.net/tan_handsome/article/details/79371076　　　　scipy 层次聚类