对模型进行评估时，可以选择很多种指标，但不同的指标可能得到不同的结果，如何选择合适的指标，需要取决于任务需求。
正确率与错误率
正确率：正确分类的样本数/总样本数，accuracy
错误率：错误分类的样本数/总样本数，error
正确率+错误率=1
这两种指标最简单，也最常用
缺点
1. 不一定能反应模型的泛化能力，如类别不均衡问题。
2. 不能满足所有任务需求
如有一车西瓜，任务一：挑出的好瓜中有多少实际是好瓜，任务二： 所有的好瓜有多少被挑出来了，显然正确率和错误率不能解决这个问题。
查准率与查全率
先认识几个概念
正样本/正元组：目标元组，感兴趣的元组
负样本/负元组：其他元组
对于二分类问题，模型的预测结果可以划分为：真正例 TP、假正例 FP、真负例 TN、 假负例 FN,
真正例就是实际为正、预测为正，其他同理
显然 TP+FP+TN+FN=总样本数
混淆矩阵
把上面四种划分用混淆矩阵来表示
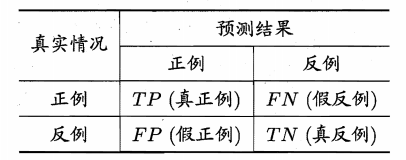
从而得出如下概念
查准率：预测为正里多少实际为正，precision，也叫精度
查全率：实际为正里多少预测为正，recall，也叫召回率
查准率和查全率是一对矛盾的度量。通常来讲，查准率高，查全率就低，反之亦然。
例如还是一车西瓜，我希望将所有好瓜尽可能选出来，如果我把所有瓜都选了，那自然所有好瓜都被选了，这就需要所有的瓜被识别为好瓜，此时查准率较低，而召回率是100%，
如果我希望选出的瓜都是好瓜，那就要慎重了，宁可不选，不能错选，这就需要预测为正就必须是真正例，此时查准率是100%，查全率可能较低。
注意我说的是可能较低，通常如果样本很好分，比如正的全分到正的，负的全分到负的，那查准率、查全率都是100%，不矛盾。
P-R曲线
既然矛盾，那两者之间的关系应该如下图
这条曲线叫 P-R曲线，即查准率-查全率曲线。
这条曲线怎么画出来的呢？可以这么理解，假如我用某种方法得到样本是正例的概率（如用模型对所有样本进行预测），然后把样本按概率排序，从高到低
如果模型把第一个预测为正，其余预测为负，此时查准率为1，查全率接近于0，
如果模型把前2个预测为正，其余预测为负，此时查准率稍微降低，查全率稍微增加，
依次...
如果模型把除最后一个外的样本预测为正，最后一个预测为负，那么查准率很低，查全率很高。
此时我把数据顺序打乱，画出来的图依然一样，即上图。
既然查准率和查全率互相矛盾，那用哪个作为评价指标呢？或者说同时用两个指标怎么评价模型呢？
两种情形
1. 如果学习器A的P-R曲线能完全“包住”学习器C的P-R曲线，则A的性能优于C
2. 如果学习器A的P-R曲线与学习器B的P-R曲线相交，则难以判断孰优孰劣，此时通常的作法是，固定查准率，比较查全率，或者固定查全率，比较查准率。
通常情况下曲线会相交，但是人们仍希望把两个学习器比出个高低，一个合理的方式是比较两条P-R曲线下的面积。
但是这个面积不好计算，于是人们又设计了一些其他综合考虑查准率查全率的方式，来替代面积计算。
平衡点：Break-Event Point，简称BEP，就是选择 查准率=查全率 的点，即上图，y=x直线与P-R曲线的交点
这种方法比较暴力
F1 与 Fβ 度量
更常用的方法是F1度量
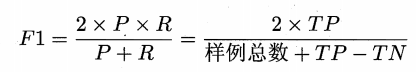
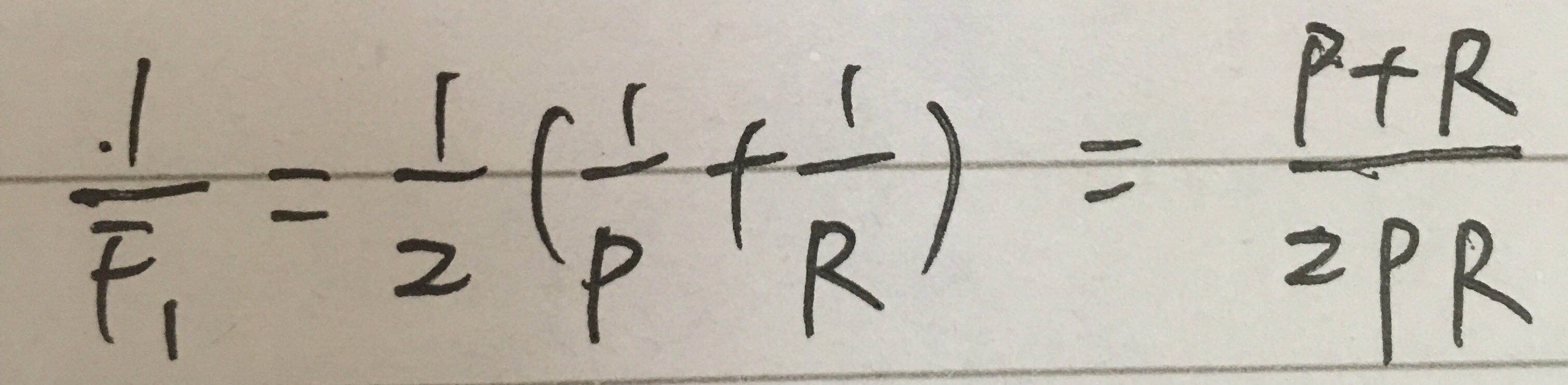
即 F1 是 P 和 R 的调和平均数。
与算数平均数 和 几何平均数相比，调和平均数更重视较小值。
在一些应用中，对查准率和查全率的重视程度有所不同。
例如商品推荐系统，为了避免骚扰客户，希望推荐的内容都是客户感兴趣的，此时查准率比较重要，
又如资料查询系统，为了不漏掉有用信息，希望把所有资料都取到，此时查全率比较重要。
此时需要对查准率和查全率进行加权
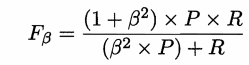
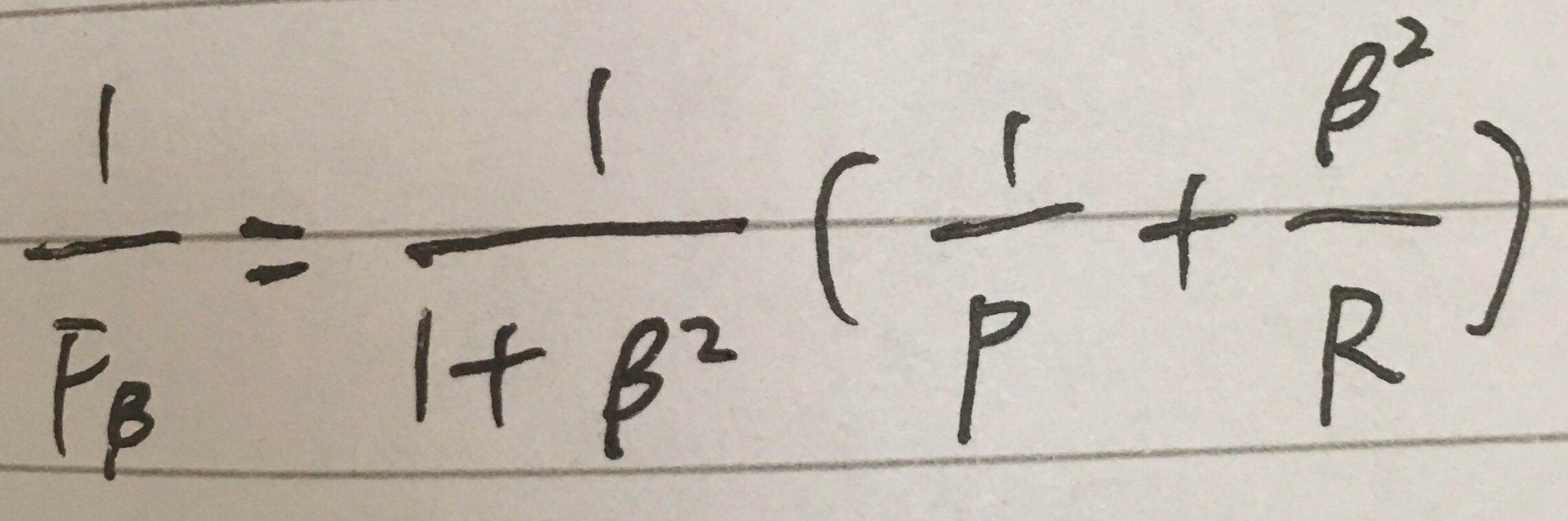
即 P 和 R 的加权调和平均数。
β>0，β度量了查全率对查准率的重要性，β=1时即为F1
β>1，查全率更重要，β<1，查准率更重要
多分类的F1
多分类没有正例负例之说，那么可以转化为多个二分类，即多个混淆矩阵，在这多个混淆矩阵上综合考虑查准率和查全率，即多分类的F1
方法1
直接在每个混淆矩阵上计算出查准率和查全率，再求平均，这样得到“宏查准率”，“宏查全率”和“宏F1”
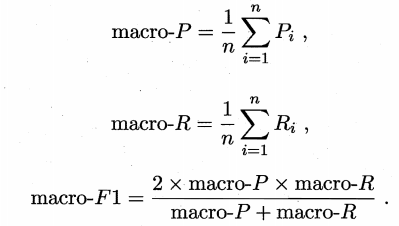
方法2
把混淆矩阵中对应元素相加求平均，即 TP 的平均，TN 的平均，等，再计算查准率、查全率、F1，这样得到“微查准率”，“微查全率”和“微F1”
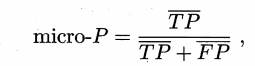
ROC 与 AUC
很多学习器是为样本生成一个概率，然后和设定阈值进行比较，大于阈值为正例，小于为负例，如逻辑回归。
而模型的优劣取决于两点：
1. 这个概率的计算准确与否
2. 阈值的设定
我们把计算出的概率按从大到小排序，然后在某个点划分开，这个点就是阈值，可以根据实际任务需求来确定这个阈值，比如更重视查准率，则阈值设大点，若更重视查全率，则阈值设小点，
这里体现了同一模型的优化，
不同的模型计算出的概率是不一样的，也就是说样本按概率排序时顺序不同，那切分时自然可能分到不同的类，
这里体现了不同模型之间的差异，
所以ROC可以用来模型优化和模型选择，理论上讲 P-R曲线也可以。
ROC 曲线
ROC曲线的绘制方法与P-R曲线类似，不再赘述，结果如下图
横坐标为假正例率，即 把 负例 识别为 正例 占 负例 的比率，FP/(FP+TN)；
// 假正例率反映了精度，假如假正例率为0，也就是说没有把负例识别为正例，也就是说识别为正例的都是正例，那精度就是 100%
纵坐标为真正例率，即 把 正例 识别为 正例 占 正例 的比率，TP/(TP+FN)，其实就是召回率；
曲线下的面积叫 AUC；
ROC 曲线说明了一个问题：TP 增加时，FP 也增加；
怎么理解呢？当我们 接受 更多的好东西时，就一定也接受了更多的坏东西，比如改革开放，引进先进技术的同时，也引入了歪风邪气；
ROC 评价
1. 若学习器A的ROC曲线能包住学习器B的ROC曲线，则A优于B
2. 若学习器A的ROC曲线与学习器B的ROC曲线相交，则难以比较孰优孰劣，此时可以比较AUC的大小
3. 根据需求确定不同的曲线，如门脸锁，我们要确保外人绝对不能进入，也就是宁可漏，不可错，
此时我们需要关注的是 FP 极低 的情况下，TP 高，如下图
假正例率为 0，代表精度 100%，此时我们追求 真正例率更高，就是在 精度 100%的情况下追求召回率更高，也就是不可错，且尽量少漏
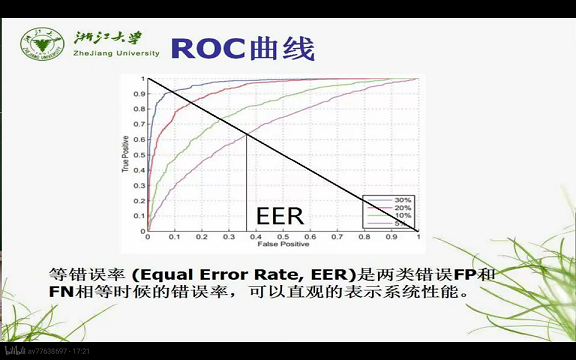
5. EER
总结
1. 模型评估主要考虑两种场景：类别均衡，类别不均衡
2. 模型评估必须考虑实际任务需求
3. P-R 曲线和 ROC曲线可以用于模型选择
4. ROC曲线可以用于模型优化
参考资料：
周志华《机器学习》
