特征选择

特征选择顾名思义就是从众多特征中选出和目标相关的特征，它是机器学习中很重要的一个环节。

 

子集选择与评价

从众多特征中选出部分特征构成特征的一个子集，就叫子集选择，

子集特征是否能很好地表征目标，需要对子集特征进行评价。

子集选择可以有前向搜索、后向搜索和双向搜索三种方式。

前向搜索

假定给定特征集{a1，a2，a3...ad}

第一轮，把每个特征看做一个子集，对每个子集进行评价，选出最优子集，假定为{a2}

第二轮，把{a2}作为基础子集，每次加入一个特征，然后进行评价，选出最优的二元子集，假定为{a2，a4}

重复上步骤

如果在某轮中，逐次添加完特征，评价结果都低于上一轮的结果，则结束，以上轮特征为最终结果。

后向搜索

与前向搜索类似，起初是全部特征作为一个集合，每轮减少一个特征。

双向搜索

相当于是两个线程，一个线程前向搜索，一个线程后向搜索，两个线程之间互相通信，在后向搜索中被删除的不会用于前向搜索，在前向搜索中被添加的不会用于后向搜索

 

这是一种贪心搜索，不一定全局最优，比如某轮特征子集为{a2，a4}，然后添加a5比a6效果好，于是新的子集{a2，a4，a5}，但是在下一轮中，有可能{a2，a4，a5}与其他特征的组合效果都不如{a2，a4，a6，a9}，

可以借助ε-贪心策略进行缓解。

 

子集评价

总体思路：假定离散属性的分类问题，根据特征子集对样本进行划分，看划分的结果与真实标签的一致性，准确率越高，子集选择的效果越好。

在这种思路下衍生了很多方法：

信息熵与信息增益：同决策树里的概念，根据属性子集划分样本，计算分裂前与分裂后的信息熵，相减得到信息增益，增益越大，效果越好。

 

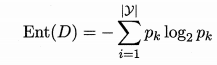
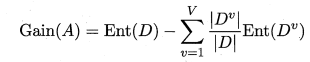
事实上，决策树也可以用于特征选择，建树时所有分裂特征就是特征子集，而且树模型都可以进行特征选择。

 

常见的特征选择方法可以分为三大类：过滤式（filter），包裹式（wrapper），嵌入式（embedding）

过滤式选择

先进行特征选择，再训练学习器 

Relief 是一种著名的过滤式选择方法，它用一个“相关统计量”来度量特征的重要性，该统计量是一个向量，向量中每个元素对应一个特征，特征子集的重要性由子集中特征对应的统计量之和来决定。

在特征选择时，可以设置阈值，也可以设定特征个数，取topk

 

具体做法

给定数据集，对每个样本xi在同类样本中找最近邻xi,nh，称为“猜中近邻”，在异类样本中找最近邻xi,nm，称为“猜错近邻”，

然后计算每个属性j的统计量

diff是一种度量，如距离

若j为离散属性，则 两样本j属性相等时，diff=0，不相等时，diff=1

若j为连续属性，则 diff=|x1-x2|，注意属性需要规范到[0,1]之间。

若xi与其猜中近邻xi,nh在属性j上的差小于xi与其猜错近邻xi,nm在属性j上的差，说明属性j在类别区分时是有益的，故增大该属性的统计量，

若xi与其猜中近邻xi,nh在属性j上的差大于xi与其猜错近邻xi,nm在属性j上的差，说明属性j在类别区分时有负作用，故减小该属性的统计量。

 

迭代所有样本，所有特征，就能算出这个统计量。可以看出计算量很大，在实际应用中，可以通过采样来近似这个统计量。

 

Relief是为二分类设计的，其扩展体 Relief-F可以实现多分类。

思路与二分类相似，二分类只找一个异类，多分类则是找到所有异类的“猜错近邻”

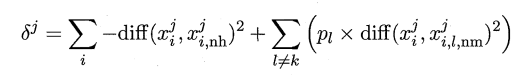
pl是每个类别的占比

 

方差选择法

from sklearn.feature_selection import VarianceThreshold
vt = VarianceThreshold(threshold = 1)
vt = vt.fit_transform(data)

 

包裹式选择

随机选择特征子集，用最终要使用的学习器的性能作为评价准则，也就是说子集是为学习器量身定制的。

所以通常包裹式选择最终模型的性能高于过滤式选择，但是由于要多次训练学习器，开销远大于过滤式选择。

 

LVW （Las Vegas Wrapper）是一种典型的包裹式选择方法，它在拉斯维加斯方法框架下采样随机策略选择子集，并用学习器的性能作为评价标准

具体做法

解释

1. E 错误率，初始无穷大，找最小

2. d 特征个数

3. A*最终的子集

4. t 迭代次数，初始为0

8. 基于子集A'的数据集进行交叉验证，得到模型误差

9. 如果误差小于当前误差，或者误差相等，但是特征个数小于当前特征个数，替换当前值

 

由于是随机生成子集，所以可能有无穷多个子集，而且每次需要训练学习器，开销很大，所以在有限时间内可能无法得到最终子集。

 

嵌入式选择

特征选择与训练学习器同时进行，当模型训练好后，特征选择也完成了。

它其实是基于模型参数的特征选择。

如线性回归 y=w1x1+w2x2+w3x3，x的系数代表了特征的重要性。

当然可以加入正则项，使得参数更平缓，L1和L2都可以。

但是L1更好，因为L1更容易使得参数更稀疏，即更容易得到0参数，用过正则的话很容易理解

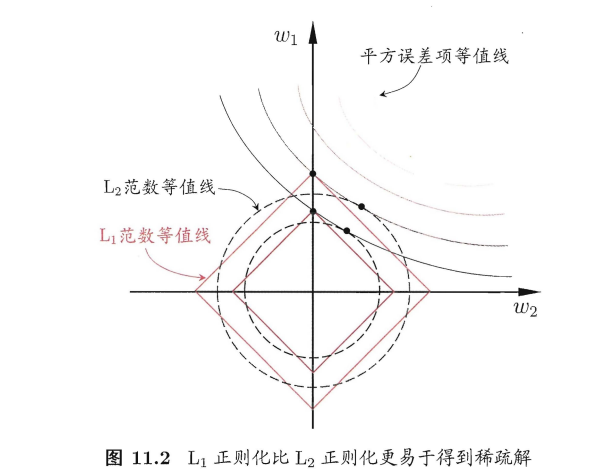
可以看到 L1曲线更容易和损失函数相交于坐标轴上，此时参数为0

 

基于上述理论，形成了很多融合特征选择方法，具体参考 ‘参考资料3’

 

 

参考资料：

周志华《机器学习》

https://blog.csdn.net/chocolate_chuqi/article/details/81284702

https://blog.csdn.net/a1368783069/article/details/52048349　　融合方法