类别不均衡问题就是不同类别的样本数差别很大，很容易理解，不再赘述。
这种情况会导致模型的误判，比如2分类，正例998，反例2，那么即使我们所有的样本都识别为正例，正确率高达99.8%，然而并没有什么卵用。
对于类别不均衡问题，大体上主要有两种，即以数据为中心驱动和以算法为中心的解决方案。
数据策略
以数据为中心的类别不均衡解决方法主要有两种：过采样和欠采样。过采样试图为少数类别生成人工数据点，而欠采样旨在消除多数类别的样本。
算法策略
算法层面的策略，特别是在深度学习领域，主要侧重于开发损失函数来应对类不平衡问题，而不是直接操纵数据。一种简单的方式便是为每个类别都设置相应的权重，以便与多数类别相比，少数类别样本的错误分类受到更严重的惩罚。另一种方法是为每个训练样本自适应地设置一个唯一的权重，以便硬样本获得更高的权重。
具体有以下几种解决方法
想办法搞到更多数据
换个模型评价方式
在类别均衡时，accuracy是比较能说明问题的，但是类别不均衡时，就会出现上文描述的问题，此时可借助其他评价指标，如精度precision和召回率recall，F1_score，详见我的其他博客。
换树模型
基于参数迭代的模型容易受到类别不均衡问题的影响，如神经网络，树模型不太受这种情况的影响
数据重组
1. 欠采样
随机删掉一些样本
这样训练速度快，但是模型准确率降低，一般不建议采用
2. 过采样
复制样本
这样做很容易过拟合
实际操作时可以慢慢增加样本数，然后观察效果，不一定非得1:1
也可以采用SMOTE算法来避免过拟合，即通过对训练集里的正例进行插值产生额外的正例
阈值移动
这个方法不如过采样、欠采样那么流行，但是在二分类问题上表现的相当成功。
我们在做分类模型时，总是把样本的分布当做总体的分布，也就是说总体上正负样本概率相同，比如男女，样本概率也相同，都是0.5，
那么在分类时，0.5一边是一类，另一边是另一类，
但是当总体正负样本概率不同时，比如正常人和病人，样本概率也不同，是病人的概率明显小的多，那是病人的概率是多少呢？ 病人数/总人数，肯定不是0.5，我们记为x，
那么在分类时，x一边是一类，另一边是另一类，
此时的x相对于0.5发生了移动。
我们y代表正例的概率，则1-y代表反例的概率，y/1-y=正样本数/负样本数，
当样本数相同时 y=0.5，
当样本数不同时 y!=0.5，可以根据上式求出，相对于0.5肯定发生了位移，这就是阈值移动。
也可以这么理解，x=0为分界线，x小于0为梨，x大于0为苹果，但是梨比较多。
那么可以将阈值x=0向右平移
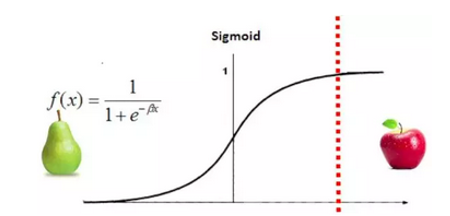
使得绝大多数预测结果为梨，只有一些特殊的情况，及其确定的时候预测为苹果。
实际上训练数据很难代表总体特征，所以我们拿样本来估计总体会有一定偏差。
Focal Loss
说到类别不均衡的损失函数，不得不提的便是 Focal Loss。对于分类问题，大家常用的便是交叉熵损失 BCE Loss，该损失函数对所有类别均一视同仁，即赋予同等的权重学习。而 Focal Loss 主要就是交叉熵损失改进的，通过引入 和 两个调节因子来调整样本数量和样本难易程度，以便模型专注于学习少数类。具体公式如下：
参考资料：
周志华《机器学习》
https://www.cnblogs.com/Determined22/p/5772538.html
https://www.jianshu.com/p/ecbc924860af smote算法
