激活函数就是非线性函数，常用于非线性模型，特别是神经网络；
非线性函数用于构建非线性决策边界，多个非线性函数的组合能够构建复杂的决策面；
本文旨在总结这些函数，并进行对比分析
阶跃函数
最早的激活函数，图如下
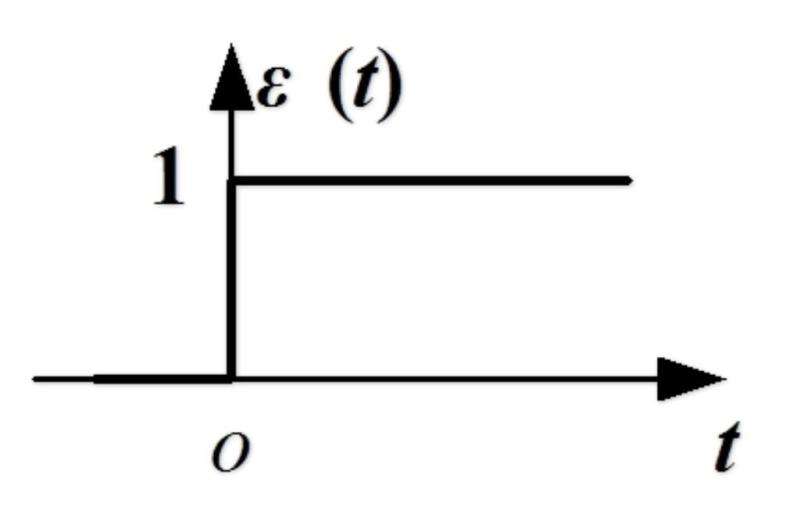
缺点：不连续，且局部导数为 0，无法反向传播
它只用在 感知器 上
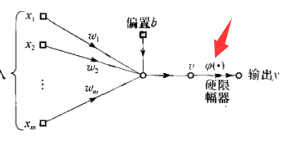
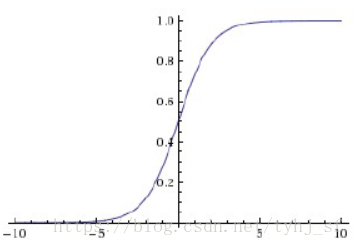
sigmoid
它是用来替代 阶跃函数的，图如下，有没有发现长得很像
计算公式如下
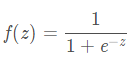
优点：
1. 有个很好的性质，即 f'(x) = f(x)[1-f(x)]，这样求导就很方便了，无需额外计算
2. 把信号压缩在 01 之间，使得信号值连续，且数值变小
缺点：
sigmoid 在深度学习中几乎被弃用，最大的问题是容易梯度消失，因为
a) sigmoid 在两侧梯度趋于 0，且在大部分 x 上，其对应的梯度趋近于 0，只有中间一小部分，梯度明显，但是你敢指望 x 取到这么小个区间？
b)sigmoid 梯度最大为 x=0 时，此时梯度值为 f(0)[1-f(0)] = 0.25，最大才 0.25，岂不是很容易消失
下图为 sigmoid 导数图
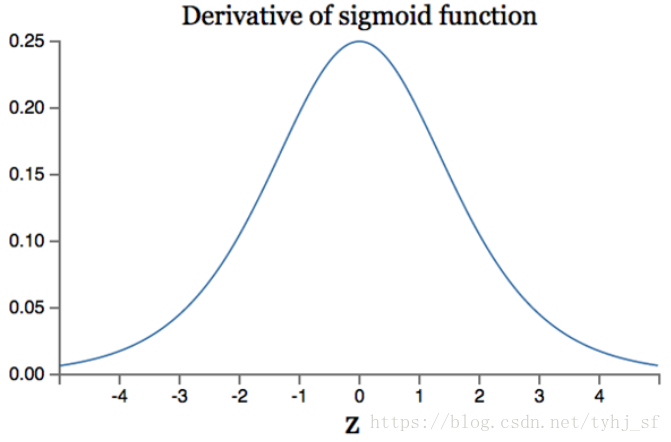
最大 0.25，abs(x)>4，梯度几乎为 0 了
还有一些不太致命的缺点：
1. 冥函数，计算耗时，增加训练时间
2. 输出不是 0 均值，即 zero-centered，若 x>0，则 f(x)>0，梯度也大于 0，两个 大于0 相乘 仍然大于0，这样 w 就一直往一个方向调整，收敛缓慢；
当然 batch 可以缓解这个问题
3. 在梯度较大的区域，也就是中间那块，模型趋于线性
tanh
双曲正切，图如下(左)
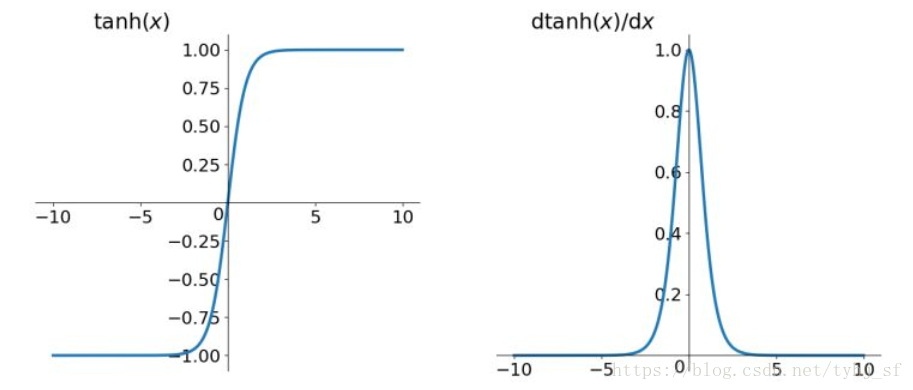
表达式
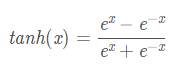
优点：
1. 解决了 sigmoid 的 非0均值问题
2. 它的求导也很方便，f'(x) = 1-f2(x)
缺点：同 sigmoid 一样，梯度消失
ReLu
在深度学习中应用最广的激活函数，图如下
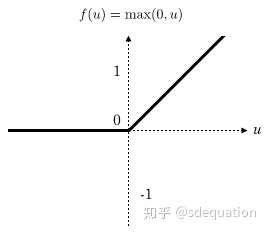
他本质是个分段线性模型，多个 relu 可以构建非线性决策面
优点：
1. 避免梯度消失
2. 求导极其方便，只需判断 是否大于0，计算速度快
3. 梯度恒为1，收敛速度快 【sigmoid 梯度最大才 0.25】
4. ReLU关闭了右边，从而会使得很多的隐层输出为0，即网络变得稀疏，起到了类似L1的正则化作用，可以在一定程度上缓解过拟合。
缺点：
1. relu 的输出也不是 zero-centered
2. Dead Relu Problem，指的是某些神经元永远不被激活，导致相应的参数永远不被更新， 导致这种情况的原因大致有两种
a) 初始化参数不当，比较少见
b) learning rate 设置过大，导致参数更新过快，不幸陷入这种状态
解决方法是可以采用 Xavier 初始化方法，以及避免将 learning rate 设置太大或使用 adagrad 等自动调节 learning rate 的算法
目前在深度学习中是最常用的激活函数
Leaky Relu
与 relu 很相似，relu 的右边是 0，leaky relu 的右边避免了 0 的出现，向下偏移了一个很小的角度，使得梯度和输出均不为 0， 图如下
表达式 f(x)=max(αx,x) α 是小于 1 的正数
优点：
一定程度上避免了 relu 的问题
Softplus
数学表达式
值域 (0, +∞)
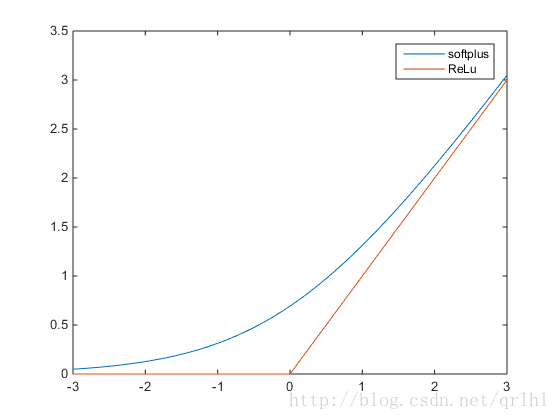
softplus可以看作是ReLu的平滑
Mish
ReLU 在负值的时候直接截断，会造成梯度的损失，Mish 为光滑的非单调激活函数
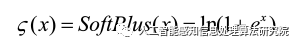
当值为负时允许较小的负梯度流入，保证了信息的流动的同时稳定了网络梯度流，起到了强正则化的作用；
允许更多的信息深入神经网络，Mish替代 ReLU 能提高网络的精确率和泛化能力。
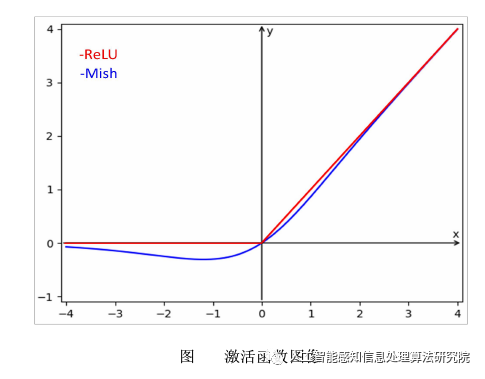
Gelu
GELU（Gaussian Error Linear Unit）
GELU可以看作是一种sigmoid和ReLU的混合体，具有如下公式：
其中，x是输入，pi是圆周率，tanh是双曲正切函数。
gelu 更平滑，收敛更稳定，有助于提升模型性能；
输入为负时不会都置为0，这样可能导致梯度消失；
输入为正数时，比 sigmoid、tanh 产生更强的非线性响应，
在实际任务中，使用GELU函数的模型通常比使用ReLU函数的模型表现更好，尤其是在自然语言处理和计算机视觉任务中。
代码
# -*- coding: utf-8 -*- # @Time : 2021/7/30 11:01 上午 # @Author : Ada import numpy as np import matplotlib.pyplot as plt import torch def gelu_1(x): #使用numpy实现 return 0.5*x*(1 + np.tanh(np.sqrt(2/np.pi)*(x + 0.044715*x**3))) def gelu_dao(inputs): return ((np.tanh((np.sqrt(2) * (0.044715 * inputs ** 3 + inputs)) / np.sqrt(np.pi)) + ((np.sqrt(2) * inputs * ( 0.134145 * inputs ** 2 + 1) * ((1 / np.cosh( (np.sqrt(2) * (0.044715 * inputs ** 3 + inputs)) / np.sqrt(np.pi))) ** 2)) / np.sqrt(np.pi) + 1))) / 2 def plot_gelu(): x1=np.arange(-8,8,0.1) y1=gelu_1(x1) #plt.plot(x1,y1) y2=gelu_dao(x1) plt.plot(x1,y2) plt.show() if __name__ == '__main__': plot_gelu()
参考资料：
https://blog.csdn.net/tyhj_sf/article/details/79932893
https://blog.csdn.net/God_68/article/details/85262255
https://zhuanlan.zhihu.com/p/609897428 gelu
https://zhuanlan.zhihu.com/p/394465965 gelu
