【蓝桥杯训练】第四天1285、1290

1285

[蓝桥杯2016初赛]寒假作业

现在小学的数学题目也不是那么好玩的。
看看这个寒假作业：

每个方块代表1~13中的某一个数字，但不能重复。
比如：
6 + 7 = 13
9 - 8 = 1
3 * 4 = 12
10 / 2 = 5
以及：
7 + 6 = 13
9 - 8 = 1
3 * 4 = 12
10 / 2 = 5
就算两种解法。（加法，乘法交换律后算不同的方案）
你一共找到了多少种方案？
输出
请填写表示方案数目的整数。

注意

每个方块代表1~13中的某一个数字，但不能重复

算法

1. 首先考虑 乘 的组合，有：
   2 * 3 = 6
   2 * 4 = 8
   2 * 5 = 10
   2 * 6 = 12
   3 * 4 = 12
2. 乘与除互逆，加与减也是，所以要考虑其中不能出现同一个数。乘除满足题意的有2 * 5 = 10与3 * 4 = 12，
   那么还剩下1 6 7 8 9 11 13
3. 组成加减满足题意的有 1 + 8 = 9 和 6 + 7 = 13
4. 最终乘除可以交换，即是2 * 5=10 and 12 / 4 = 3或者10 / 5=2 and 3 * 4= 12，加减法也是，然后有可以交换的，结果为2^6 = 64

扩展：如何产生全排列

法1：
使用Python的itertools.permutations,返回一个生成器对象，遍历他，循环变量为一个元组，函数的参数是可迭代对象，如list，tuple，str都可以

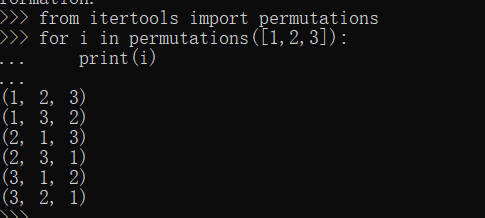
法2：
自定义函数实现,自左向右循环的交换，交换的次数为len(iter)!-1
实现自动获取更新下一个排列：

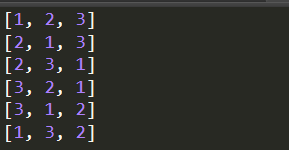
def next_permu(data):
    global ptr
    if ptr == -1:
        ptr = (ptr+1) % (len(data)-1)
        return
    else:
        data[ptr],data[ptr+1] = data[ptr+1],data[ptr]
        ptr = (ptr+1) % (len(data)-1)

ptr = -1
a = [1,2,3]
for i in range(6):
    next_permu(a)
    print(a)

题解

答案：64

1290

[蓝桥杯2016初赛]煤球数目

有一堆煤球，堆成三角棱锥形。具体：
第一层放1个，
第二层3个（排列成三角形），
第三层6个（排列成三角形），
第四层10个（排列成三角形），
....
如果一共有100层，共有多少个煤球？
输出
请填表示煤球总数目的数字。

注意

求100层的总和

算法

1. 很显然第n层的数目为n*(n+1)/2
2. 那么前100层总和即可以用递归求解

题解

def f(n):
    if n == 1:
        return 1
    return f(n-1)+singleLaw(n)
singleLaw = lambda n:n*(n+1)/2
print(int(f(100)))