能够自平衡的【红黑树】,必知必会
红黑树
红黑树(英语:Red–black tree)是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。它是在1972年由鲁道夫·贝尔发明的,他称之为”对称二叉B树”,它现代的名字是在Leo J. Guibas和Robert Sedgewick于1978年写的一篇论文中获得的。它是复杂的,但它的操作有着良好的最坏情况运行时间,并且在实践中是高效的:它可以在 O(logn)时间内做查找,插入和删除,这里的n是树中元素的数目,摘自:维基百科-红黑树。
特点(需要满足的规则)
- 每个节点非红即黑;
- 根节点总是黑色的;
- 每个叶子节点都是黑色的空节点(NIL节点);
- 如果节点是红色的,则它的子节点必须是黑色的(反之不一定);
- 从根节点到叶节点或空子节点的每条路径,必须包含相同数目的黑色节点(即相同的黑色高度)
例如: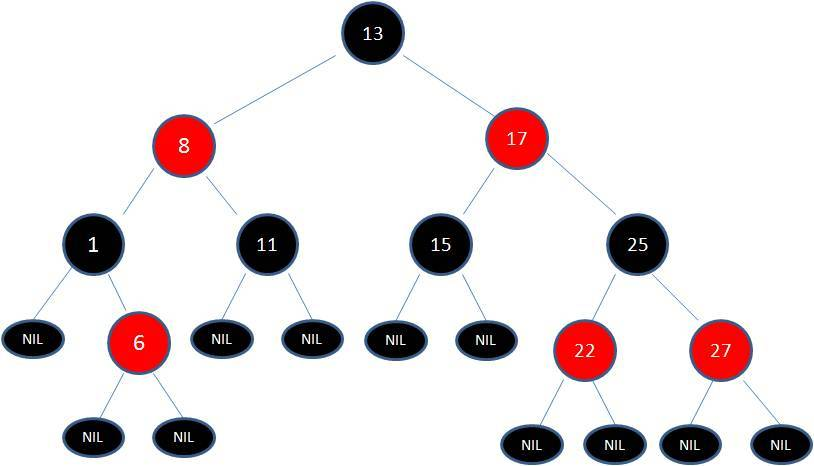
在我看来:
- 除开NIL结点,看图的颜色,不难发现从root开始黑红交替;
- 只有在叶子结点和NIL结点可能出现两个黑色结点,除开这种,没有连续的红(黑)结点连续。
红黑树的修正
1. 变色
变色仅仅指的是红黑树节点的变色。因为红黑树节点必须是【红】或者【黑】这两中颜色,所以变色只是将当前的节点颜色进行变化,以满足特性(2,3,4,5)。
2. 旋转
旋转分左旋和右旋。图片一看就懂。
-
左旋
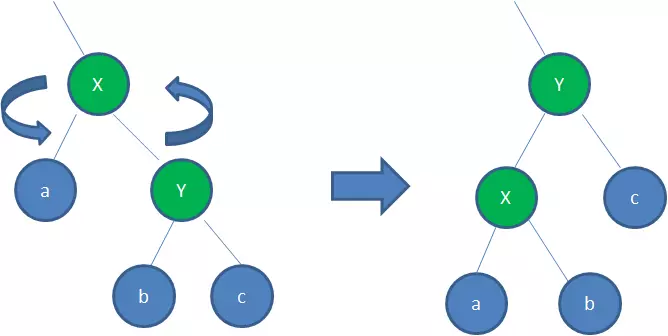
-
右旋
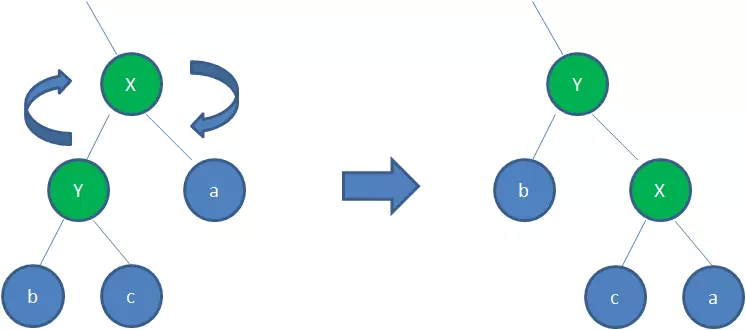
应用
TreeMap、TreeSet以及JDK1.8之后的HashMap底层都用到了红黑树。
推荐阅读
- 漫画:什么是红黑树?(墙裂推荐,也讲到了平衡二叉树)
- 红黑树深入剖析及Java实现(美团点评技术部门)
谢谢阅读!
纯粹于当下,执着于理想。


