【笔记】机器学习 - 李宏毅 - 5 - Classification
Classification: Probabilistic Generative Model 分类:概率生成模型
如果说对于分类问题用回归的方法硬解,也就是说,将其连续化。比如 \(Class 1\) 对应的目标输出为 1, \(Class 2\) 对应 -1。
则在测试集上,结果更接近1的归为\(Class 1\),反之归为\(Class 2\)。
这样做存在的问题:如果有Error数据的干扰,会影响分类的结果。
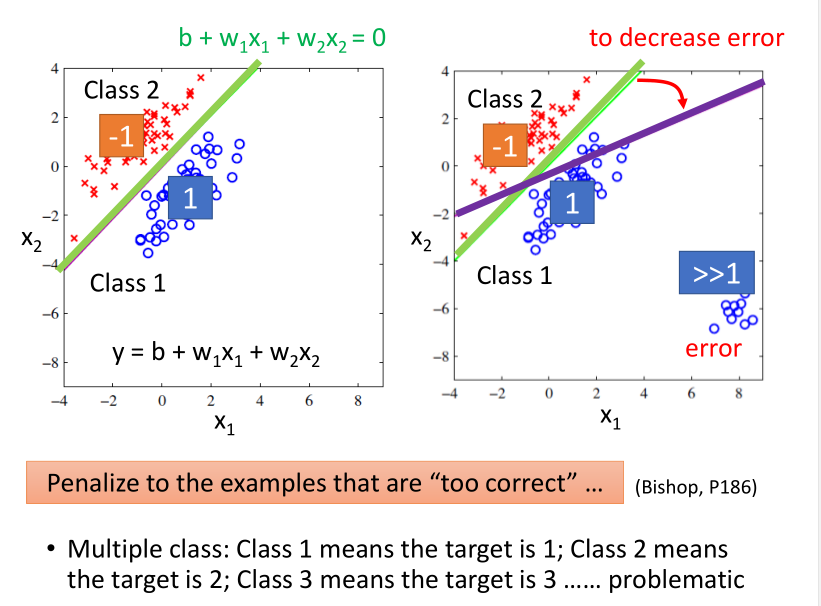
还有就是,如果是多分类问题,则在各类之间增加了线性关系,比如认为 \(Class 3\) 比 $ Class 4$ 离 \(Class 1\) 更近,这是不对的。
另一种方法是,用\(if\)函数,不过这样的话,虽然分类更合理,但损失函数无法微分计算。

比较好的模型是概率生成模型,通过概率方式计算,(贝叶斯公式)。
其中\(P(C_1)\)和\(P(C_2)\)是先验概率。
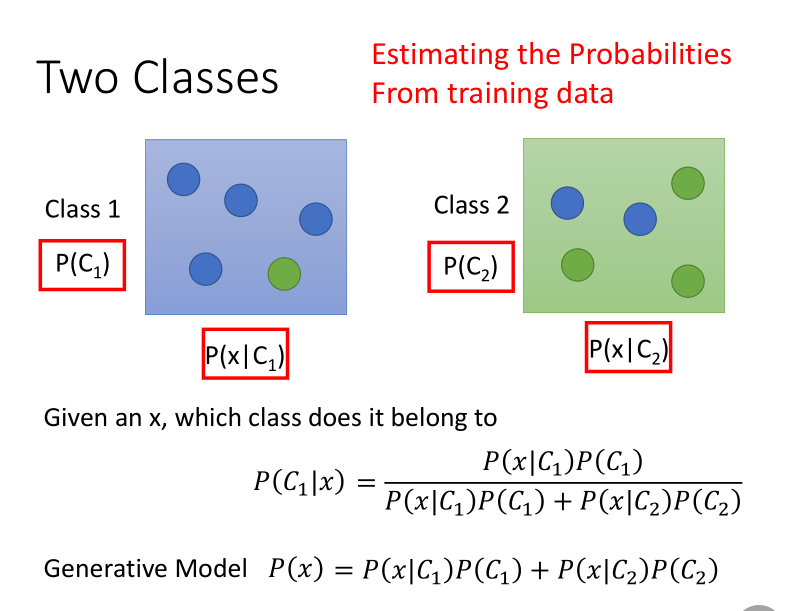
高斯分布,最大似然估计
这里选用高斯分布(其他合理的分布也可以,比如对于二元分类来说,可以假设是符合 Bernoulli distribution(伯努利分布))。
从概率上讲,任何高斯分布都可以产生样本数据,但我们需要的是最大可能性的那种分布,求出它的期望 \(\mu\) 和协方差矩阵 \(\sum\)。
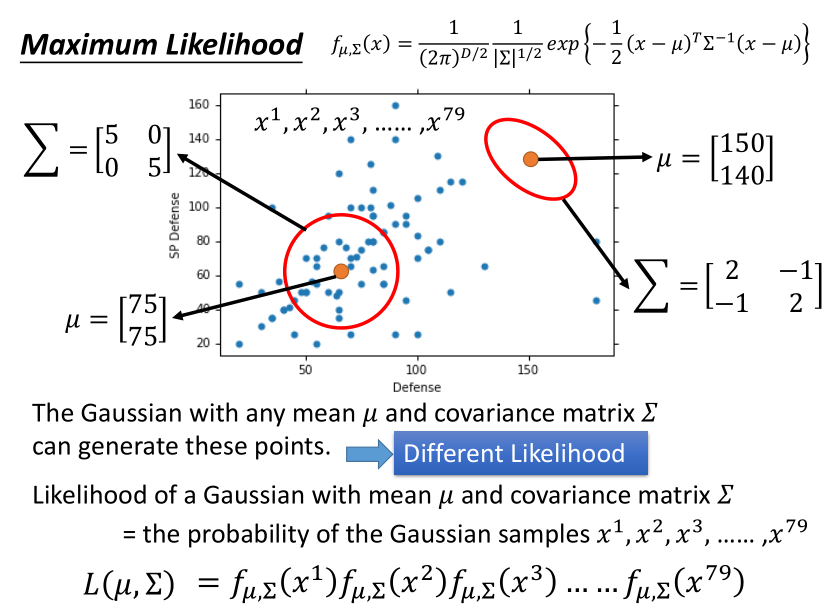
求解方法就是对 \(\mu\)和\(\sum\)分别关于\(L(\mu, \sum)\)求偏微分。

最后得到的结果不是很好,只有47%正确率,即使考虑更多的参数(Overfitting),提升到7维,也只有54%。
如果说,给两个高斯分布相同的协方差矩阵(求加权平均值)的话,效果会好很多,达到了73%。因为分界线是直线,所以也把这种分类叫做线性模型。

分类问题的机器学习三步骤:

此外,假设每一个维度用概率分布模型产生出来的几率是相互独立的,所以可以将 \(P(x|C_1)\)拆解,可以认为每个 \(P(x_k|C_1)\)产生的概率都符合一维的高斯分布。
也就是此时P(x|C1)的高斯分布的协方差是对角型的(不是对角线的地方值都是0),这样就可以减少参数的量。但是结果显示这种做法不好。
这种假设所有的feature都是相互独立产生的分类叫做 Naive Bayes Classifier(朴素贝叶斯分类器)。

后验概率


经过一系列数学推导后,最后在形式上转换为了 \(w · x + b\),然后再套一个\(sigmoid\)函数就得到了最后的结果。
所以,在训练时可以直接去求w和b,这在形式上和回归模型又统一了。




