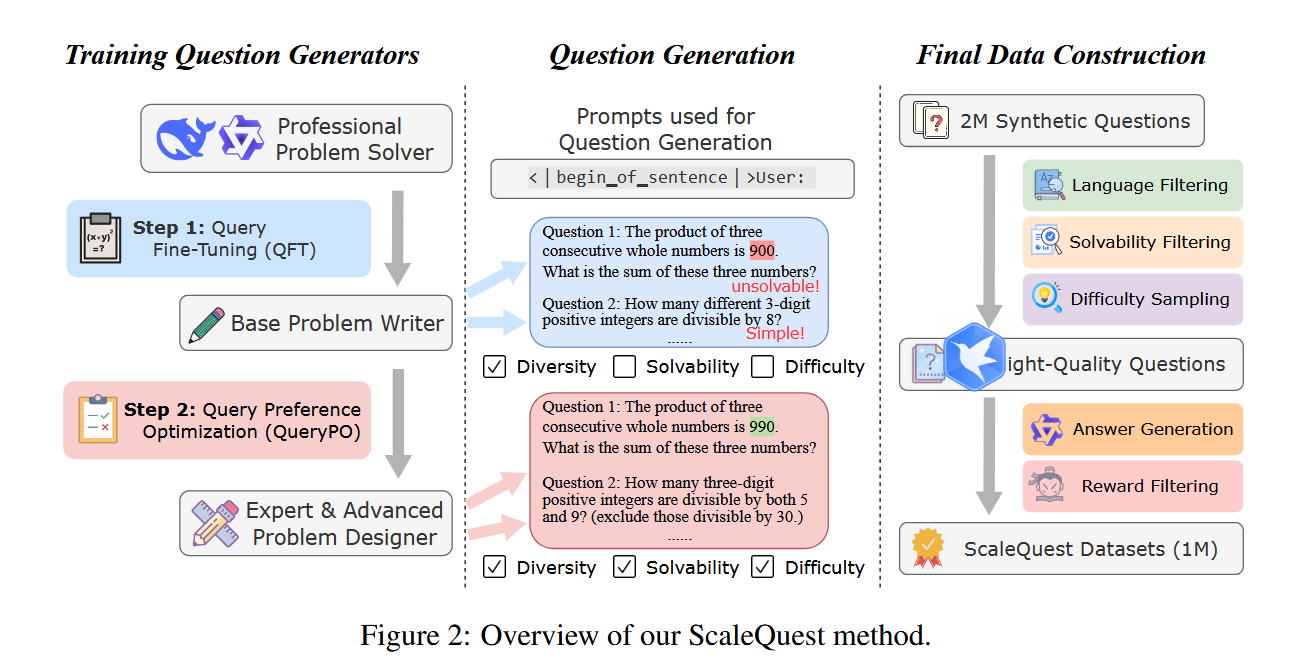
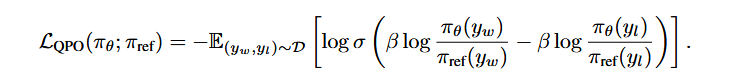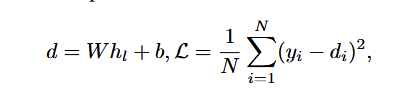Unleashing Reasoning Capability of LLMs via Scalable Question Synthesis from Scratch
1. 概述
LLM的SFT数据合成工作不可避免的可以划分为多个阶段：
- 指令合成
- 响应合成
- 数据筛选。
本篇文章采用了传统LLM的训练过程（SFT+DPO）进行数据合成。
在领域专有模型（DeepSeekMath7B-RL，Qwen2-Math-7BInstruct）的基础上，
- 指令合成：通过QFT（即SFT）使得模型能够正确的生成要求的指令，再通过QPO（即DPO）的方式使得模型生成的指令更加精致（更困难 or 可以解决）
- 指令筛选：语言筛选（统一用英文）、可解决性筛选（保证问题可解决）、困难性筛选（筛选出过于简单的问题）
- 响应合成：通过领域专有模型（Qwen2-Math-7B-Instruct）进行Response生成
- 响应筛选：启发式规则筛选 + RM（InternLM2-7B-Reward）打分筛选
效果：部分metric逼近甚至超过闭源模型。
2. 方法
2.1 Qustion Fine-Tunning(QFT)
基座模型：SFT基于领域专有模型（DeepSeekMath-7B-RL、Qwen2-Math-7BInstruct）。
目的：使基座模型摒弃之前的习惯（根据Prompt生成Response），仅生成Question，不需要学习具体的知识分布等信息
SFT数据主要包括两部分：
- Prompt
- Response
Prompt部分仅使用：
<|begin of sentence|>User:
Response部分：
从GSM8K和MATH两个数据集中筛选了15K的数据。对于这部分数据执行了如下操作：
- 丢弃solution
- question尾部添加终止字符，表示生成结束。
2.2 QFT验证部分
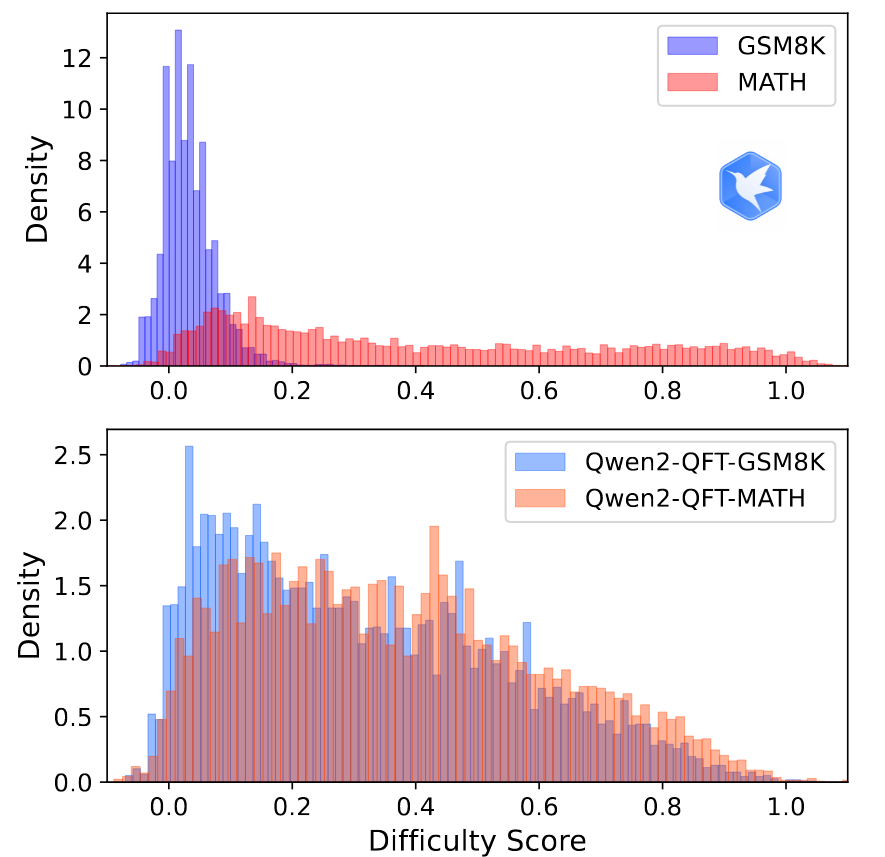
笔者基于GSM8K和MATH分别对Qwen2-Math-7B进行QFT，生成两个模型：Qwen2-QFT-GSM8K and Qwen2-QFT-MATH。分别用这两个模型生成了10K的问题。问题难度分布如下图：
其中上面的部分是GSM8K和MATH数据集的问题难度分布，下面部分是合成数据的问题难度分布。难度评估标准在后面赘述细节。
可以看到合成数据的问题难度分布与训练数据集完全无关，基本达到SFT的预期（不是从领域专业模型中蒸馏问题）。
2.3 QPO
问题：QFT后的模型生成的Question存在两个方向的问题：
- 可解决性(生成的Question本身就是现实世界中不可能的，例如 1+1怎么等于3这种。)
- 困难性（生成的Question太简单了）
目标：优化上述两种情况
DPO数据构造：
- 负向数据：QFT后的模型，生成10K的Question
- 正向偏好数据：通过GPT-4o-mini对负向数据进行优化（两个方向），得到的结果作为正向偏好数据。
笔者实验了Qwen2-Math-7BInstruct和GPT-4o-mini作为正向偏好数据的生成器，对优化结果采用GPT-4o进行评估（Prompt见附录4.1.3, 4.1.4）。
- 可解决性方向同时使用了两者进行优化，可以发现GPT-4o-mini完胜。（Prompt见附录4.1.1）
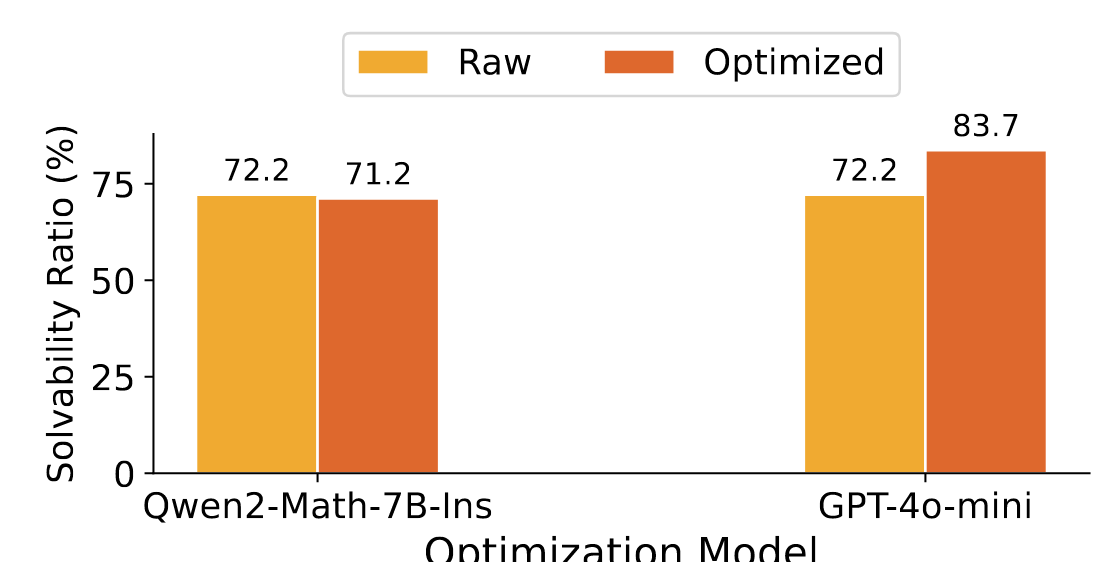
- 困难性方向仅用了GPT-4o-mini进行优化，在复杂度上也有明显提升（Prompt见附录4.1.2）
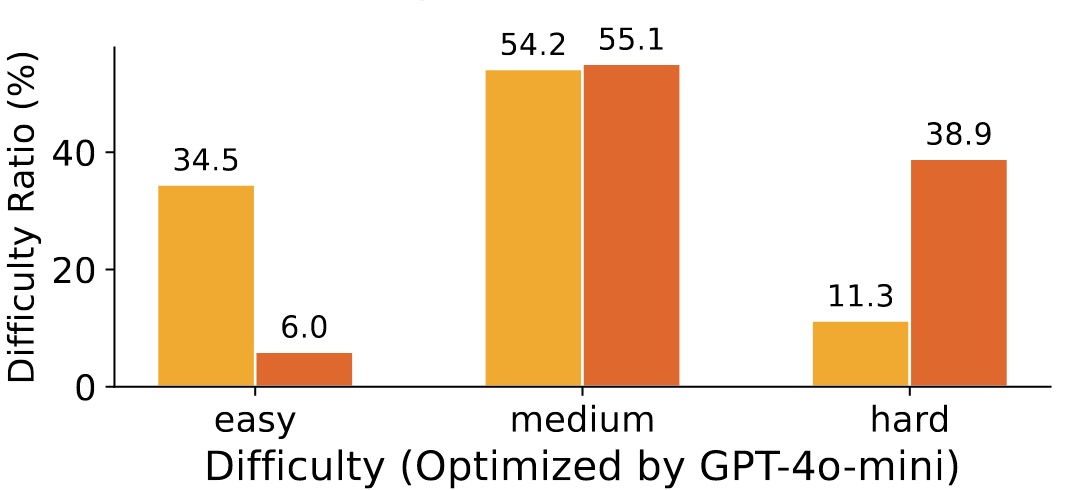
因此，正向偏好数据使用GPT-4o-mini进行合成的。
DPO loss的设置：
其中\(y_w\)是正向偏好数据，\(y_l\)是负向数据。
2.4 问题筛选
2.4.1 语言筛选
仅保留英文问题。
2.4.2 可解决性筛选
尽管进行了DPO，合成数据仍存在不可解决现象，主要包括：
- 缺失条件、冗余条件、逻辑不一致导致的约束不佳类问题
- 现实世界不符的问题（例如，计算人数出现负数）
解决方式：double chek，通过Qwen2-Math-7B-Instruct再验证一次可解决性，Prompt为附录4.1.3所示
2.4.3 困难性采样
困难度打分是通过对同一问题，采用DeepseekMath-7B-RL模型进行回答，采样n次，其中回答的失败率进行打分的，失败率越高，表示问题越困难。
通过上面的方式对GSM8K和MATH进行打分，然后基于DeepseekMath-7B-Base训练了一个分类器，即在模型的最后一层后添加了一个打分模块。
其中\(h_l\)表示DeepseekMath-7B-Base的最后一层隐藏层，\(W\)和\(b\)是最后打分模块的权重和bias（毕竟单层神经网络的表达式为\(y=Wx+b\)），\(L\)表示loss,是预测分数和真值分数的MSE。
最后实际上对于DeepSeekMath-QGen仅筛选掉了极简单的问题，对于Qwen2Math-QGen没有进行额外筛选
2.5 结果生成和评估
结果生成使用的模型：Qwen2-Math-7B-Instruct
生成方式：
（1）同一个问题生成5个Response，推理出正确答案的即被使用。（我猜测如果5个Response都是正确答案，应该也是RM打分）
（2）如果没有正确答案生成，则使用出现频率最高的答案作为正确答案，然后收集这个答案的所有Response作为候选集合。最后用RM获取候选集合中最优秀的。RM用的是InternLM2-7B-Reward。
3. 实验
本文通过以DeepSeekMath-7B-RL、Qwen2-Math-7BInstruct为基座，通过QFT和QPO生成了两个模型：
- Deepseek-QGen
- Qwen2-Math-QGen
进而通过这两个模型一共生成了1M（一共生成了2M，筛选后剩下1M）的问题，其中400K来自Deepseek-QGen，600K来自Qwen2-Math-QGen。然后通过第2章中的方法生成Response，构建了1M的SFT数据。
然后使用这部分数据对4个模型进行了SFT。分别是：
- Mistral-7B
- Llama3-8B
- DeepSeekMath-7B
- Qwen2-Math7B
评估标准：使用难度递增的4个数据集：
- GSM8K
- MATH
- College Math
- Olympiad Bench
比较零样本下 pass@1 （1次回答就准确的比率）。
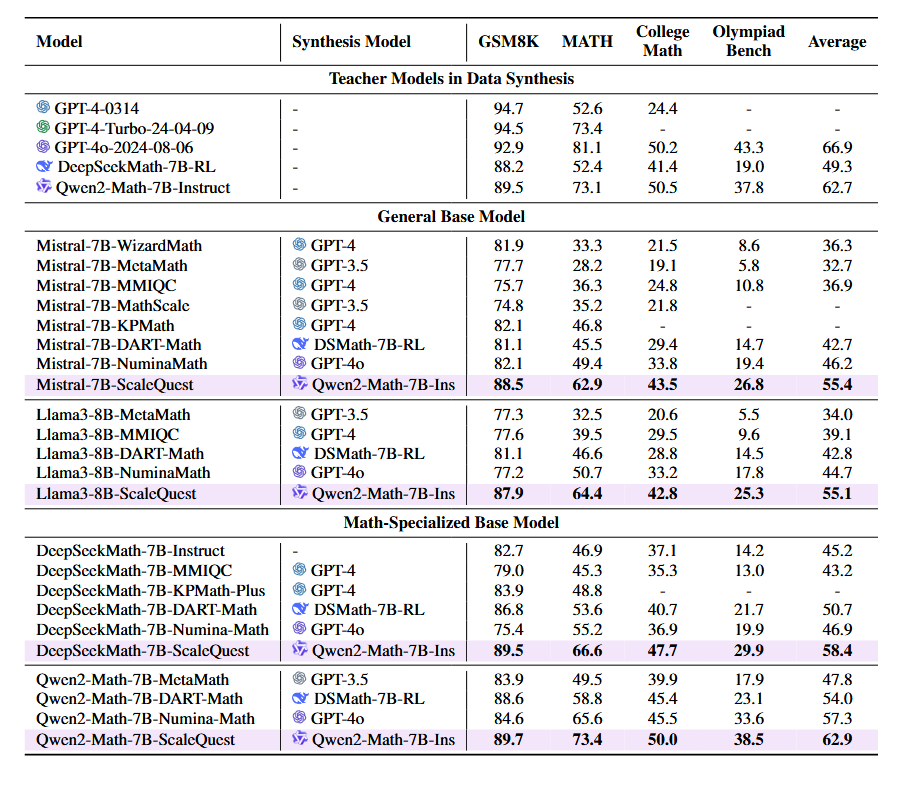
结果如下：
- 效果最优，超越了之前的数据合成方法，甚至可以媲美闭源大模型（GPT-4系列）
- ScaleQuest随着数据量增大效果提升。（这部分，我没太看懂原论文的解释，太数学领域了），主要好似是看LLama-8B的那部分，数据集的size是不断上升的。
3.1 消融实验
注意：以下3个实验，不是在同一基座模型上SFT的，这是一个特别的点。
3.1.1 子步骤的有效性
Raw:通过指令进化的方式，生成新的问题和Response（这里没有细说，生成了1M的数据，保证数据量一致），使用的是Qwen2-Math-7B-Instruct。
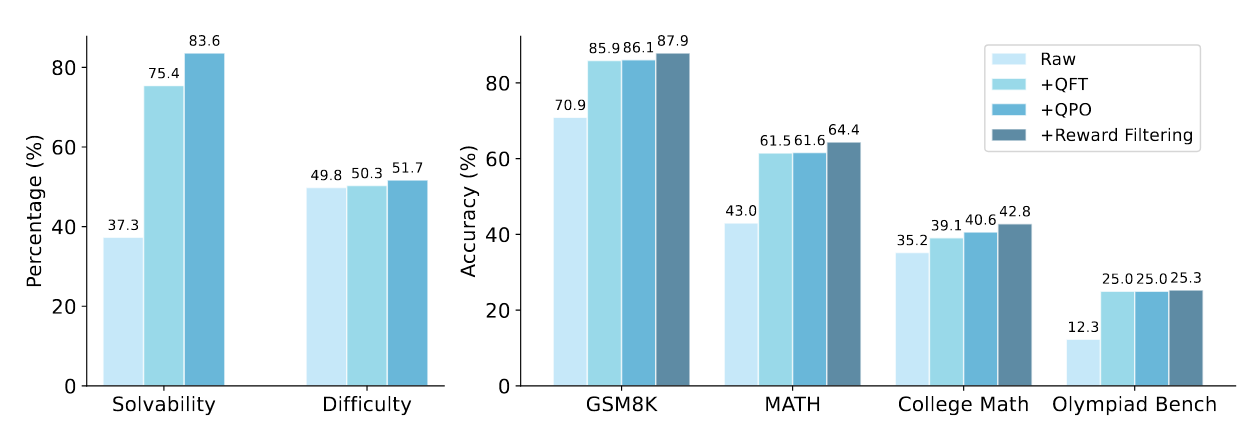
左图是使用GPT-4o-mini 为不同模型生成问题的可解决性和困难性进行打分。 可以看到每一步都是有提升的。
右图是通过Raw、QFT、QPO、数据过滤，这四个过程生成的1M数据，对LLama3-8B微调，在4个数据集上的效果，也可以看到每一步都是有提升的。
3.1.2 问题生成的有效性
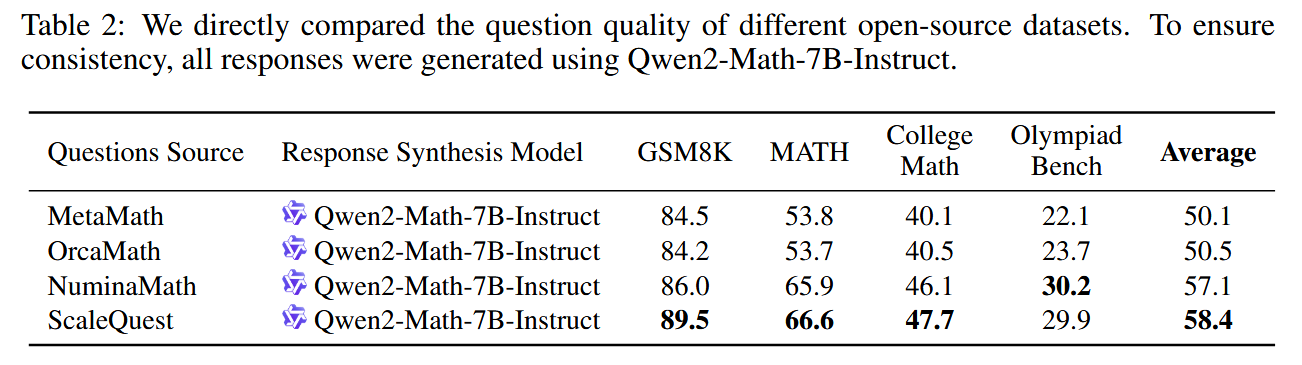
笔者对3个开源数据集（MetaMath、OrcaMath、NuminaMath）以及合成数据集ScaleQuest，保证Question不变，重新使用Qwen2-Math-7B-Instruct生成了Response。然后用这部分数据SFT了DeepSeekMath-7B，结果如下：
印证了Question生成的有效性，ScaleQuest生成的Question更优质。
3.1.3 使用多生成器提升了数据的多样性
本文使用了两个问题生成器：
- DSMath-QGen
- Qwen2-Math-QGen
分别生成了400K和600K的Question。
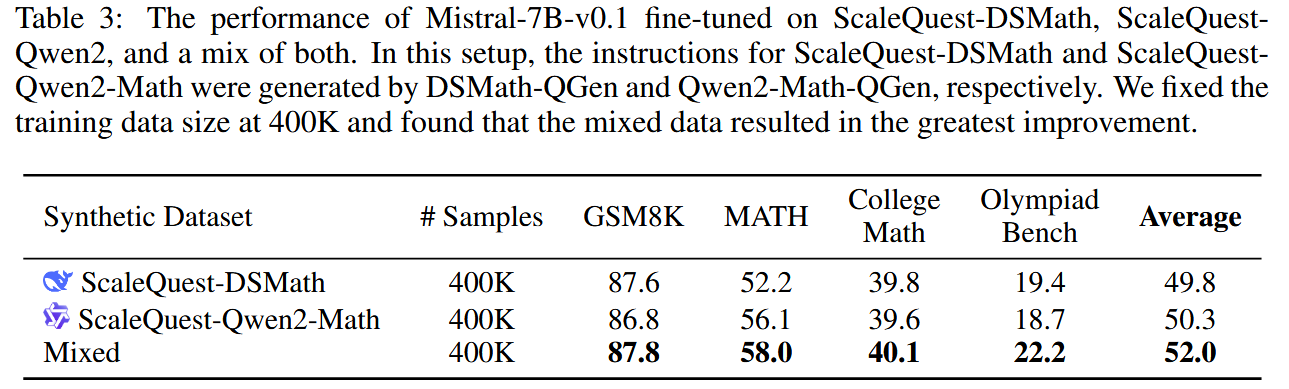
这里从两部分数据中，都只采样400K的数据，去SFT一个Mistral-7B。以及混合数据后采用400K（采样比例没提），去SFT一个Mistral-7B。效果如下：
笔者解释：
- DSMath-QGen生成的问题更简单，贴近现实
- Qwen2-Math-QGen生成的问题更复杂，具有挑战性。
进而提升了数据的多样性。
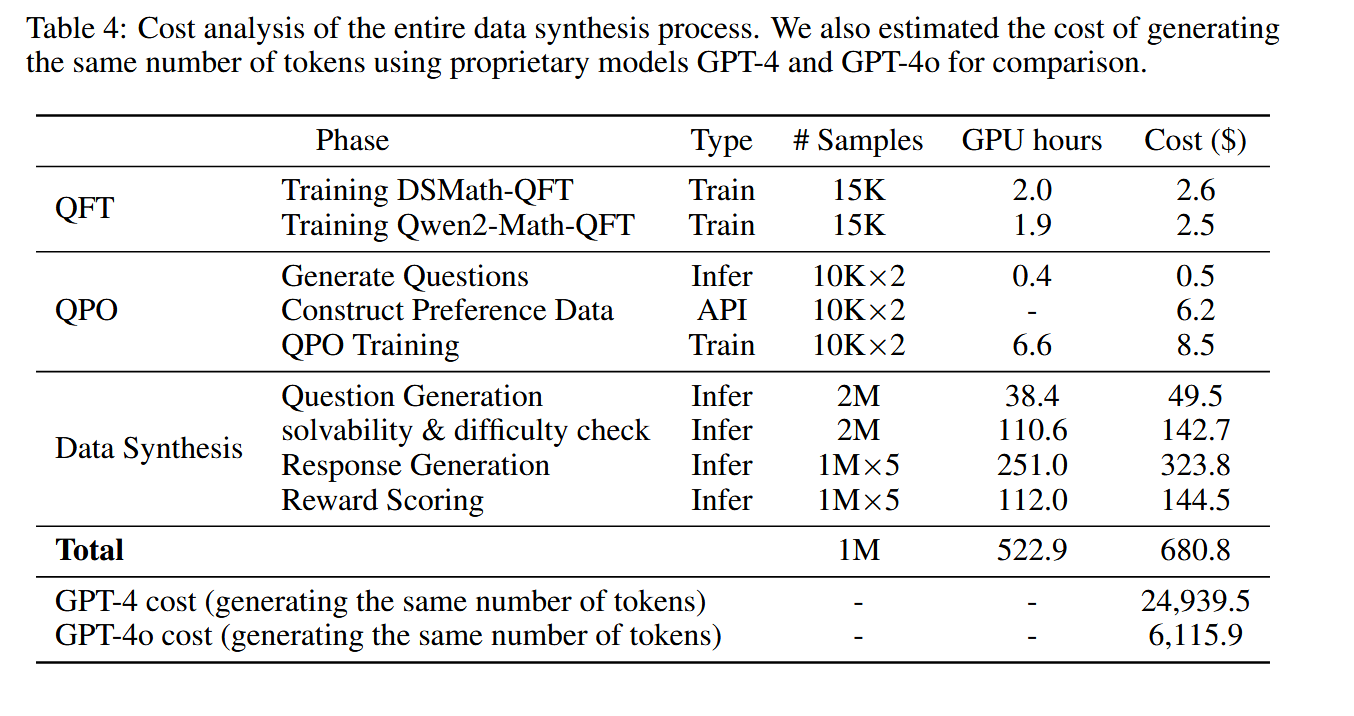
3.2 花销分析
数据合成使用了8 A100-40G-PCIe GPUs，跑了522.9 GPU hours。花销是全用GPT-4o生成同样量级数据的1/10.
4. 附录
4.1 QPO部分的Prompts
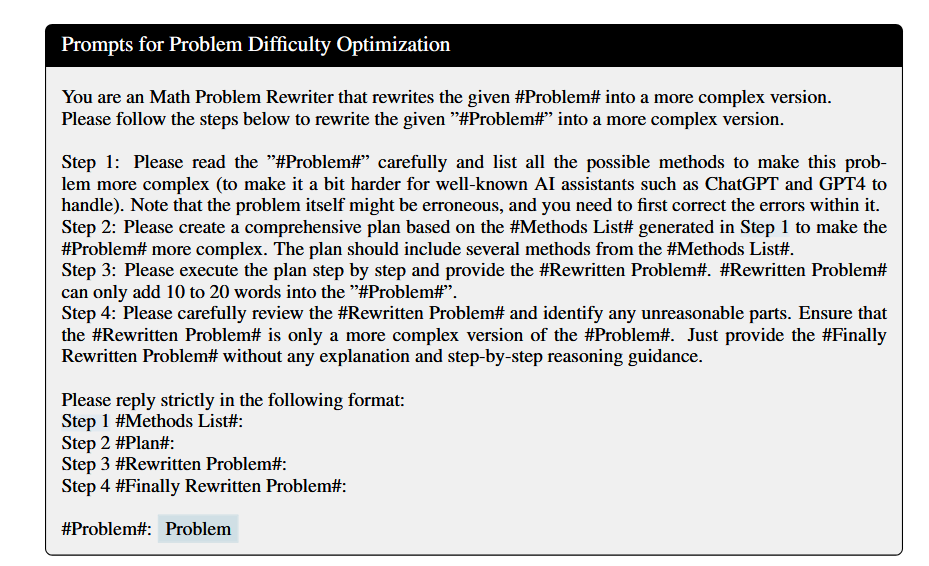
- 可解决性的优化Prompt
- 复杂性的优化Prompt
仔细看Prompt会发现和指令进化很类似。
- 可解决性检测的Prompt
- 复杂性分类的Prompt
