Leetcode刷题笔记——单调性
单调性
单调性是数学中使用的一种常见性质,通常用于描述函数,在高等数学中的定义常常为:
设函数f(x)在区间I上有定义,如果对于I上的任意两个数x1和x2,当x1<x2时,有f(x1)<f(x2)(或者f(x1)>f(x2)),则称函数f(x)在区间I上是单调递增的(或者单调递减的)。
例如如下图像就是两个单调函数。
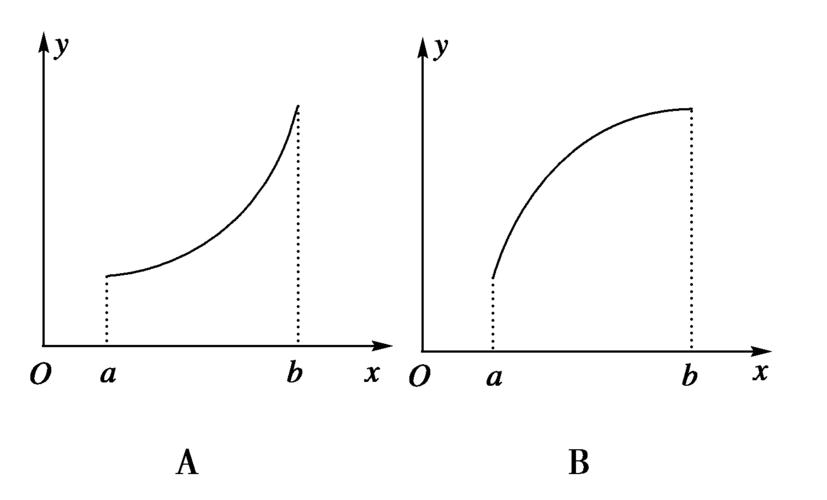
利用单调性我们可以减少很多重复的运算。例如,对于如下函数,我们给定其定义域为[0,+∞),现在要求查找出在其定义域内所有f(x)即y大于0.5的区间。
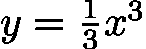
- 如果不借助单调性,我们需要采用遍历的方法,依次遍历定义域中的所有点x,判断其f(x)是否满足条件(大于0.5)。
- 如果借助单调性,我们知道上述函数是严格单调递增的,其图像如下:
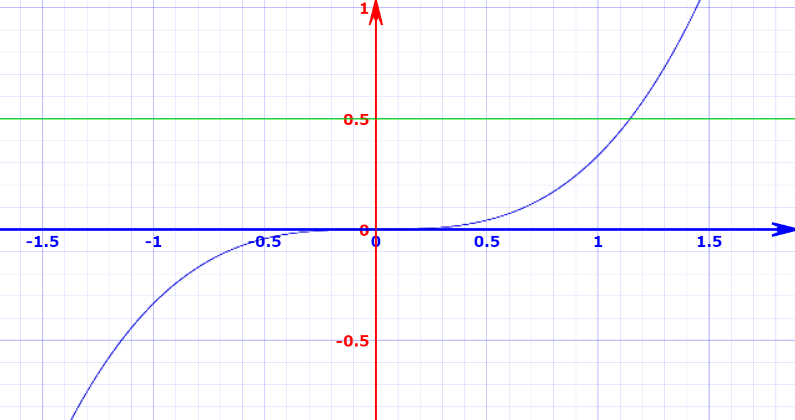
绿线表示y=0.5的图像,处理该问题,只需要找到方程0.5=(1/3)x^3的解x0,由于函数具有单调性,且单调递增,因此,所有大于x0的区间内的x其f(x)都满足大于0.5。
对于计算机语言来说,用于表示函数的常见数据结构就是数组,我们可以通过
- 原数组本身的单调性
- 构造单调性
简化许多运算。下面引入几个例子:
15. 三数之和
题目:给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。
注意:
- 答案中不可以包含重复的三元组
- 3 <= nums.length <= 3000
- -10^5 <= nums[i] <= 10^5
按照最朴素的解决方法,三层循环,循环遍历整个数组,然后再对整个结果进行去重,便可以解决该问题,但是时间复杂度为O(n^3),由于过于简单,这里给出伪代码:
list = [][]int{}
for i:=0;i <= len(nums)-3;i ++ {
for j:=i+1;j <= len(nums)-2;j ++ {
for k:= j+1;k < len(nums)-1;k ++ {
if nums[i]+nums[j]+nums[k] == 0 {
list = append(list, []int{nums[i],nums[j],nums[k]})
}
}
}
}
对list去重
本题目首先要求我们去重,因为返回结果要求不重复,对于去重常见的做法:
- 使用数据结构set、map进行处理,但是会额外占用内存
- 对原始数据排序,然后按序处理跳过重复项
优化掉去重问题后,我们可以尝试对内层的两层for循环进行优化,这里就引入了一个经典的方法:构造单调性,根据单调性进行查找。
巧妙的方法
如果nums[i]确定,那么我们只需要寻找满足条件nums[j]+nums[k]=-nums[i]的j、k值,这就变成了一个二数之和的问题,暴力算法是直接进行遍历,然后查找该值,但是由于数组的有序性,我们有一种更加巧妙的方法:
- 由于当前数组的有序性,保证了数组本身是单调递增(或递减的,这里以递增为例)
- 设置指针p1、p2指向数组开头
p1=i+1和结尾p2=len(nums)-1 - pred=nums[p1]+nums[p2],target=-nums[i]
- if target < pred,由于数组递增,nums[p2-1]<num[p2],因此,p2 --
- if target > pred,由于数组递增,nums[p1+1]>num[p1],因此,p1 ++
- if target == pred,找到了目标,但为防止遗漏数据还要继续查找,此时指针向任意方向移动都没有影响,可以p1 ++或者p2 --
- 直到p1 >p2则可以停止查找(=取决于需求,如果有需求可以>=或<=)
这个模式可以应用于很多地方,实际上具有单调性的函数一般都可以通过该办法查找,例如nums[j]*nums[k]=target,查找j、k。
例如,在[-1,0,1,2,-1, 3]这个数组中,查找nums[j]+nums[k]=4的nums[j]和nums[k]的值,现对其进行排序,然后用上述方法进行处理:
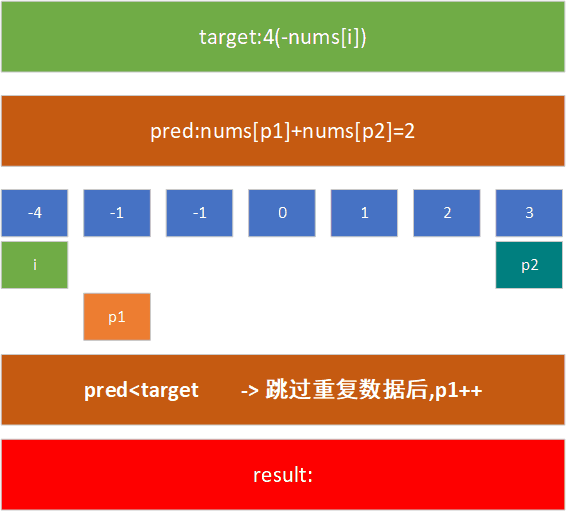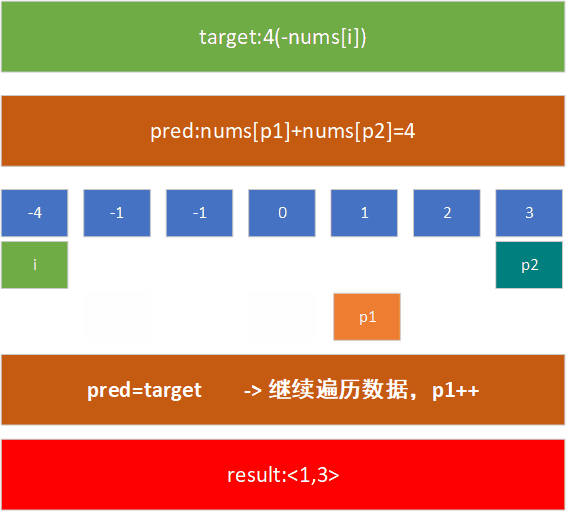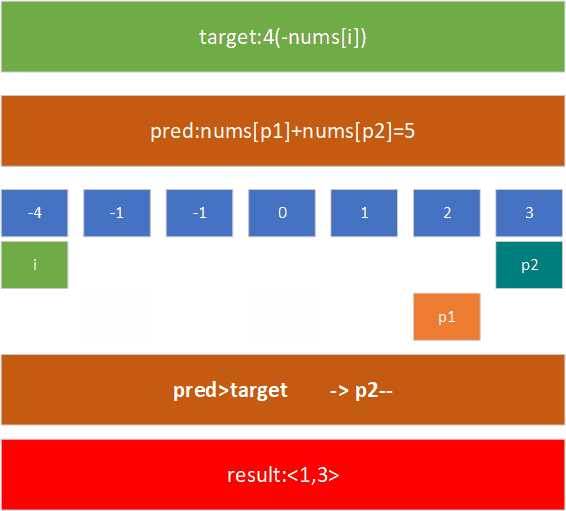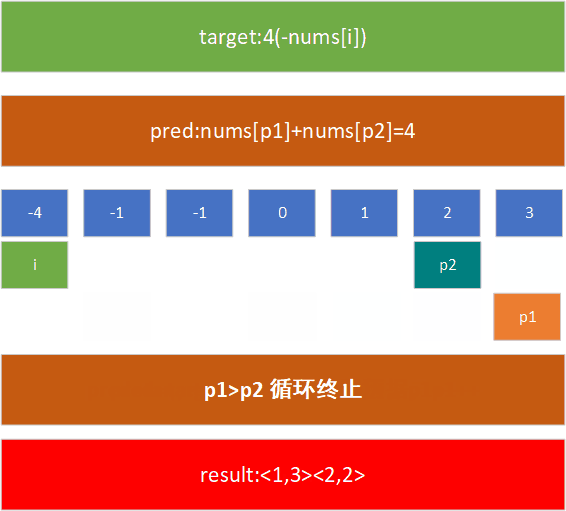
了解了这个模式后,我们给出解决该问题的代码:
解题代码以及注释
import "sort"
func threeSum(nums []int) [][]int {
result := [][]int{}
sort.Ints(nums)
// 尝试固定i,然后将3数之和转化为两数之和
for i := 0; i < len(nums)-2; i++ {
// 对nums[i]进行去重
if i-1 >= 0 && nums[i-1] == nums[i] {
continue
}
sum := -nums[i]
left := i + 1
right := len(nums) - 1
// 解决两数之和问题,寻找left、right使得nums[left]+nums[right]==sum
for left < right {
temp := nums[left] + nums[right]
if temp == sum {
result = append(result, []int{nums[i], nums[left], nums[right]})
// 去重nums[left]
for left < right && nums[left] == nums[left+1] {
left++
}
// 去重nums[right]
for left < right && nums[right] == nums[right-1] {
right--
}
left++
right--
} else if temp > sum {
right--
} else {
left++
}
}
}
return result
}
823. 带因子的二叉树
题目:给出一个含有不重复整数元素的数组arr,每个整数arr[i]均大于 1。用这些整数来构建二叉树,每个整数可以使用任意次数。其中:每个非叶结点的值应等于它的两个子结点的值的乘积。满足条件的二叉树一共有多少个?答案可能很大,返回 对 10^9+7 取余 的结果。
例如:输入: arr = [2, 4, 5, 10]
输出: 7
解释: 可以得到这些二叉树: [2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]
该问题是一个树相关的问题,并且对于父子结点处理过程是类似的。举例说明这件事:
对于输入arr=[18, 3, 6, 2],页结点可以为[2][3][6][18],可以把未显示的结点看做空结点,对于顶点为6的树可以为[6,2,3]或者[6,3,2],就需要借助叶节点信息。对于顶点为18的树可以为[18,3,6],[18,6,3],而组成以[6]的顶点的组合有3个。可以看到该问题是个动态规划问题。
f(18)=f(3)*f(6)
f(18)=f(6)*f(3)
f(6)=f(3)*f(2)
f(6)=f(2)*f(3)
f(3)=1
f(2)=1
状态转换方程为:
\(f(a*b)= \begin{array}{ll} f(a)*f(b)*2+1 & a!=b,a为左子树b为右子树,和a为右子树b为左子树\\ f(a)*f(b)+1, & a==b\\ \end{array}\)
那最后的问题就是查找在index属于[0,i-1]的数组中,哪些a,b满足arr[a]*arr[b]==arr[i],我们就可以使用上面提到的巧妙的方法类比解决该问题。这里就不再赘述。
解题代码和注释
func numFactoredBinaryTrees(arr []int) int {
sort.Ints(arr)
dp := make([]int64, len(arr))
res, mod := int64(0), int64(1e9 + 7)
for i := 0; i < len(arr); i++ {
dp[i] = 1
// 查找arr[left]*arr[right]==arr[right]*arr[left]
for left, right := 0, i - 1; left <= right; left++ {
for left <= right && int64(arr[left]) * int64(arr[right]) > int64(arr[i]) {
right--
}
if left <= right && int64(arr[left]) * int64(arr[right]) == int64(arr[i]) {
if left == right {
dp[i] = (dp[i] + dp[left] * dp[right]) % mod
} else {
dp[i] = (dp[i] + dp[left] * dp[right] * 2) % mod
}
}
}
res = (res + dp[i]) % mod
}
return int(res)
}


