11.3 afternoon


迭代40

#include<cstdio> #include<cstring> using namespace std; int n,sum,falg; char s[200010],c[200010]; void Dfs(int now){ if(now==sum+1){ int flag=0; for(int i=1;i+sum-1<=n;i++){ int f=0; for(int j=1;j<=sum;j++) if(c[j]!=s[i+j-1]){ f=1;break; } if(f==0){//都一样 flag=1;break; } } if(flag==0)falg=1;return; } c[now]='A';Dfs(now+1); if(falg)return;c[now]=' '; c[now]='B';Dfs(now+1); if(falg)return;c[now]=' '; } int main() { freopen("ab.in","r",stdin); freopen("ab.out","w",stdout); scanf("%s",s+1); n=strlen(s+1); for(sum=1;sum<=30;sum++){ Dfs(1);if(falg)break; } for(int i=1;i<=sum;i++) printf("%c",c[i]); fclose(stdin);fclose(stdout); return 0; }
位运算预处理

/* 答案很短 很短 直接搜 不过 检验的时候很慢... 预处理所有的子串 存好了就可以O(1)的检验了 因为只有AB 可以用位运算优化 */ #include<cstdio> #include<cmath> #include<cstring> #define maxn (1<<22)+10 using namespace std; int n,m,f[maxn],sum,falg,ans; char s[maxn]; void Dfs(int now,int x){ if(now==sum+1){ if(f[x]==0){ ans=x;falg=1; } return; } Dfs(now+1,x);if(falg)return; Dfs(now+1,x+(1<<now-1));if(falg)return; } int main() { freopen("ab.in","r",stdin); freopen("ab.out","w",stdout); scanf("%s",s); n=strlen(s);m=log(n)/log(2)+1; for(int i=0;i<n;i++){ int x=0; for(int j=1;j<=m;j++){ if(i+j-1>n)break; if(s[i+j-1]=='B') x+=(1<<j-1); f[x+(1<<j)]=1; } } for(sum=1;sum<=m;sum++){ Dfs(1,1<<sum);if(falg)break; } for(int i=0;i<sum;i++) if(ans&(1<<i))printf("B"); else printf("A"); fclose(stdin);fclose(stdout); return 0; }


暴力40

#include<cstdio> #include<iostream> #define bas 10000000 #define maxn 1000010 using namespace std; int p,a,b,pri[maxn],cnt,ans; bool f[bas+10]; void Get(){ for(int i=2;i<=bas;i++){ if(f[i]==0)pri[++cnt]=i; for(int j=1;j<=cnt;j++){ if(i*pri[j]>bas)break; f[i*pri[j]]=1; if(i%pri[j]==0)break; } } } int main() { freopen("prime.in","r",stdin); freopen("prime.out","w",stdout); cin>>p>>a>>b; if(p==1000000&&a==1000000000&&b==1001000000){ cout<<"433144"<<endl;return 0; } int L=max(a,p+1); int R=b;Get(); for(int k=L;k<=R;k++){ int x=k,falg=0; for(int i=1;i<=cnt;i++){ int P=pri[i]; if(P*P>x)break; if(x%P==0){ while(x%P==0)x/=P; if(P>p)falg=1; } if(x<=bas&&f[x]==0&&x>p)falg=1; if(falg==1)break; } if(x>p)falg=1;ans+=falg; } cout<<ans<<endl; fclose(stdin);fclose(stdout); return 0; }

/* 求区间内有一个质因子比p大的数的个数 存在一个 不好判 正难则反 求全部<=p的数的个数 递推 定义状态 f[l][r][x]表示 l-r区间内 所有质因子<=p的数的个数 递推的话 就是 f[l][r][x]=f[l][r][x-1]+f[ l/x ][ r/x ][x]; 还有几个边界条件 递推的话不会写顺序 写了搜索 状态太大存不下 索性不存了 嗯 本机测爆栈 不过答案应该问题不大 */ #include<cstdio> #include<cmath> #include<algorithm> #define N 1000000 using namespace std; int L,R,p,prime[N/10],num; bool f[N+10]; void Get(){ for(int i=2;i<=N;i++){ if(f[i]==0)prime[++num]=i; for(int j=1;j<=num;j++){ if(i*prime[j]>N)break; f[i*prime[j]]=1; if(i%prime[j]==0)break; } } } int Cal(int x){ int r=0; for(int i=1;i<=num;i++){ if(prime[i]*prime[i]>x)break; if(x%prime[i]==0){ while(x%prime[i]==0)x/=prime[i]; r=max(r,prime[i]); } } return max(x,r); } int Dfs(int l,int r,int x){ if(l>r)return 0; if(x==0)return l==1; if(r<=prime[x])return r-l+1; if(l==r)return Cal(r)<=prime[x]; return Dfs(l,r,x-1)+Dfs((l-1)/prime[x]+1,r/prime[x],x); } int main() { freopen("prime.in","r",stdin); freopen("prime.out","w",stdout); scanf("%d%d%d",&p,&L,&R);Get(); int pos=upper_bound(prime+1,prime+1+num,p)-prime-1; printf("%d\n",R-L+1-Dfs(L,R,pos)); fclose(stdin);fclose(stdout); return 0; }



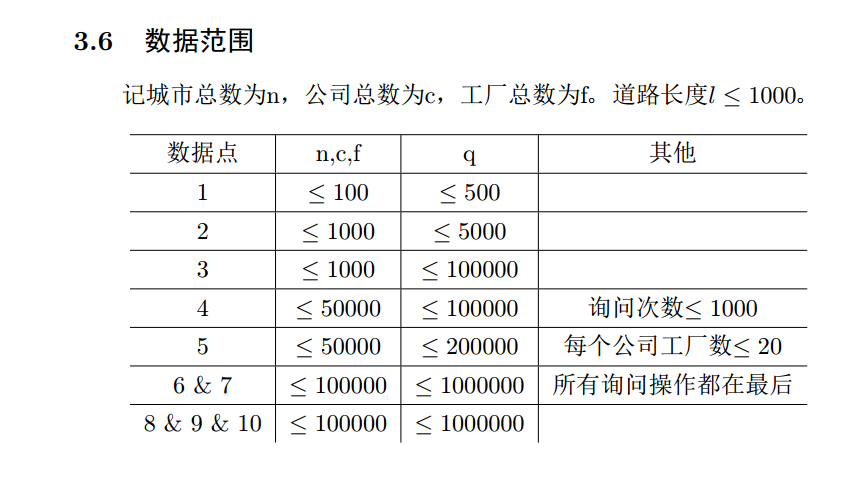
暂无正解



 浙公网安备 33010602011771号
浙公网安备 33010602011771号