一、栈

栈

栈是只能在某一端插入和删除的特殊线性表。

用桶堆积物品，先堆进来的压在底下，随后一件一件往上堆。取走时，只能从上面一件一件取。堆和取都在顶部进行，底部一般是不动的。

栈就是一种类似桶堆积物品的数据结构，进行删除和插入的一端称栈顶，另一堆称栈底。

插入一般称为进栈（PUSH），删除则称为退栈（POP）。 栈也称为后进先出表（LIFO表）。

一个栈可以用定长为Ｎ的数组Ｓ来表示，用一个栈指针TOP指向栈顶。

若TOP＝0，表示栈空，TOP=N时栈满。进栈时TOP加１。退栈时TOP减１。

当TOP<0时为下溢。栈指针在运算中永远指向栈顶。

1、进栈（PUSH）算法

①若TOP≥ｎ时，则给出溢出信息，作出错处理（进栈前首先检查栈是否已满，满则溢出；不满则作②）

②TOP++（栈指针加１，指向进栈地址）；

③S[TOP]=X，结束（X为新进栈的元素）；

2、退栈（POP）算法

①若TOP≤0，则给出下溢信息，作出错处理(退栈前先检查是否已为空栈， 空则下溢；不空则作②)；

②X=S[TOP]，（退栈后的元素赋给X）；　

③TOP--，结束（栈指针减１，指向栈顶）。

进栈、出栈的c++实现过程程序：

#define n 100
void push(int s[],int *top,int *x)  //入栈
{
   if (*top==n) printf("overflow"); 
     else { (*top)++; s[*top]=*x; }
}
void pop(int s[],int *y,int *top)   //出栈
{
   if (*top==0)  printf("underflow");  
     else { *y=s[*top]; (*top)--; }
}

对于出栈运算中的“下溢”，程序中仅给出了一个标志信息，而在实际应用中，下溢可用来作为控制程序转移的判断标志，是十分有用的。

对于入栈运算中的“上溢”，则是一种致命的错误，将使程序无法继续运行，所以要设法避免。

堆栈的数组模拟

十进制数N和其它d进制数的转换是实现计算的基本问题，解决方法很多，下面给出一种算法原理：

N=(N / d)×d＋N % d （其中 / 为整除运算，%为求余运算）。

例如：(1348)10＝(2504)8运算过程如下：

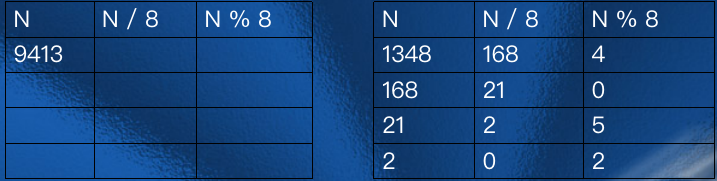
例题：

【例1】括号的匹配（表达式的合法性检查）

【问题描述】

假设一个表达式有英文字母（小写）、运算符（+，—，*，/）和左右小（圆）括号构成，以“@”作为表达式的结束符。请编写一个程序检查表达式中的左右圆括号是否匹配，若匹配，则返回“YES”；否则返回“NO”。假设表达式长度小于255，左圆括号少于20个。

【算法分析】

假设输入的字符串存储在c中（char c[256] ）。

我们可以定义一个栈：char s[maxn+1]; int top;

用它来存放表达式中从左往右的左圆括号（maxn=20）。

算法的思路为：

顺序（从左往右）扫描表达式的每个字符c[i]，若是“（”，则让它进栈；若遇到的是“）”，则让栈顶元素出栈；当栈发生下溢或当表达式处理完毕而栈非空时，都表示不匹配，返回“NO”；否则表示匹配，返回“YES”。

 #include<cstdio>
#include<cstdlib>
using namespace std;
#define maxn 20
char c[256];
bool judge(char c[256])
{ 
    int top=0,i=0;
    while (c[i]!='@') 
    {
        if (c[i]=='(') top++;
        if (c[i]==')') 
        {
           if (top>0) top--;
             else return 0;
        }
        i++;
    }
    if (top!=0) return 0;          //检测栈是否为空。不空则说明有未匹配的括号
    else return 1;
}
main()
{    
  scanf("%s",c);   
  if (judge(c))printf("YES");
  else printf("NO");
  system("pause");
  return 0;
}

【例2】编程求一个后缀表达式的值

【问题描述】

​ 从键盘读入一个后缀表达式（字符串），只含有0-9组成的运算数及加（+）、减（—）、乘（*）、除（/）四种运算符。每个运算数之间用一个空格隔开，不需要判断给你的表达式是否合法。以@作为结束标志

【算法分析】

后缀表达式的处理过程很简单，过程如下：扫描后缀表达式，凡遇操作数则将之压进堆栈，遇运算符则从堆栈中弹出两个操作数进行该运算，将运算结果压栈，然后继续扫描，直到后缀表达式被扫描完毕为止，此时栈底元素即为该后缀表达式的值。

比如，16–9(4+3)转换成后缀表达式为：16□9□4□3□+–，在字符数组A中的形式为：

栈中的变化情况：

运行结果：-47

#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
using namespace std;
int stack[101];
char s[256];
int comp(char s[256])
{
   int  i=0,top=0,x,y;
   while (i<=strlen(s)-2) 
   {
      switch (s[i])
      {
         case '+':stack[--top]+=stack[top+1]; break;
         case '-':stack[--top]-=stack[top+1]; break;
         case '*':stack[--top]*=stack[top+1]; break;
         case '/':stack[--top]/=stack[top+1]; break;
         default:x=0; while (s[i]!=' ') x=x*10+s[i++]-'0'; stack[++top]=x; break;
      }
      i++;
    }                //while
    return stack[top];
}

main()
{            
  printf("input a string(@_over):");
  gets(s);
  printf("result=%d",comp(s));
  system("pause");
  return 0;
}

栈的用途极为广泛，在源程序编译中表达式的计算、过程的嵌套调用和递归调用等都要用到栈，下面以表达式计算为例子加以说明。

源程序编译中，若要把一个含有表达式的赋值语句翻译成正确求值的机器语言，首先应正确地解释表达式。例如，对赋值语句X＝4＋8×2－3; (式 11.1)

其正确的计算结果应该是17，但若在编译程序中简单地按自左向右扫描的原则进行计算，则为：X＝12×2－3＝24－3＝21.这结果显然是错误的。

因此，为了使编译程序能够正确地求值，必须事先规定求值的顺序和规则。通常采用运算符优先数法

一般表达式中会遇到操作数、运算符和语句结束符等，以算术运算符为例，对每种运算赋予一个优先数，如：

运算符：×　÷　＋　－　

优先数：２　２　１　１（语句结束符“；”的优先数为零）

在运算过程中，优先数高的运算符应先进行运算（但遇到括号时，应另作处理）。按这样的规定，对式（11.1）自左向右进行运算时，其计算顺序就被唯一地确定下来了。计算顺序确定后，在对表达式进行编译时，一般设立两个栈，一个称为运算符栈（OPS），另一个称为操作数栈（OVS），以便分别存放表达式中的运算符和操作数。编译程序自左向右扫描表达式直至语句结束，其处理原则是：

①凡遇到操作数，一律进入操作数栈；

②当遇到运算符时，则将运算符的优先数与运算符栈中的栈顶元素的优先

数相比较；若该运算符的优先数大，则进栈；反之，则取出栈顶的运算符，并在操作数栈中连续取出两个栈顶元素作为运算对象进行运算，并将运算结果存入操作数栈，然后继续比较该运算符与栈顶元素的优先数。

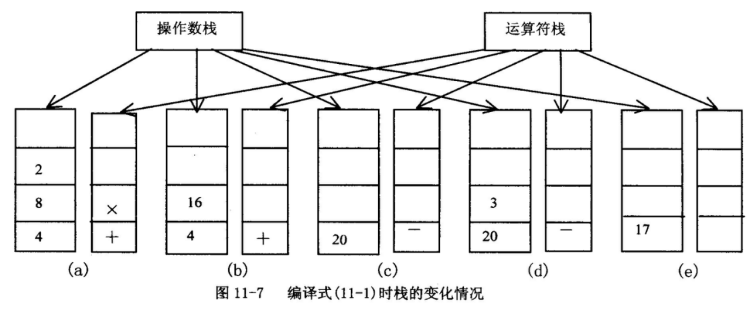
例如式（11.1）中，当扫描到“＋”和“×”时都要将运算符入栈。接着扫描到“－”号， 其优先数小于乘号所以乘号退栈，并执行８×２，将结果１６再存入操作数栈。

再将“－”号的优先数与运算符栈的栈顶元素“＋”号的优先数相比较，两者相等，所以再将加号退栈，进行４＋１６，结果为２０，再入栈，接着，由于运算栈已空，所以减号入栈。

当扫描到“３”时，操作数入栈。当扫描到“；”时，其优先数最低， 所以减号退栈并执行20-3，结果为17并入栈。因已扫描到语句结束符，所以表达式的求值结束，结果为17。

【例3】模拟计算机处理算术表达式过程。从键盘上输入算术表达式串（只含＋、－、×、÷运算符，允许含括号），输出算术表达式的值。设输入的表达式串是合法的。
【算法分析】
建立两个栈，一个是操作数栈（number），一个是运算符栈（symbol），根据运算符的优先级对两个栈进行相应的操作。

#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
using namespace std;
int  number[101],i=0, p=1;
char symbol[101],s[256], t[256];  
void push()      //算符入栈运算
{
  symbol[++p]=s[i];
}
void pop()       //运算符栈顶元素出栈,并取出操作数栈元素完成相应的运算
{
   switch (symbol[p--])
   {
      case '+':number[p]+=number[p + 1];break;
             case '-':number[p]-=number[p + 1];break;
      case '*':number[p]*=number[p + 1];break;
      case '/':number[p]/=number[p + 1];break;
   }
}
bool can()            //判断运算符的优先级别,建立标志函数
{
  if ((s[i]=='+'||s[i]=='-')&&symbol[p]!='(') return 1;
  if ((s[i]=='*'||s[i]=='/')&&(symbol[p]=='*'||symbol[p]=='/'))return 1;
  return 0;
}
main()
{  
  printf("String :");gets(s);
  s[strlen(s)]=')';symbol[p]='(';
  while (i<strlen(s))      
{
      while (s[i]=='(')            //左括号处理
      {
          push();i++;
      }
      int x=0;
          while (s[i]>='0'&&s[i]<='9')  //取数入操作数栈
         x=x*10+s[i++]-'0';
      number[p]=x;
      do
      {  
          if (s[i]==')')            //右括号处理
          {
            while (symbol[p]!='(') pop();
            number[--p]=number[p + 1];
            }
          else
          {                   //根据标志函数值作运算符入栈或出栈运算处理
            while (can()) pop();
            push();
          }
        i++;
      }while (i<strlen(s)&&s[i-1]==')');
  }
  printf("Result=%d", number[0]);
  system("pause");
  return 0;
}