九、深度优先搜索算法

深度优先搜索

从起点出发，走过的点要做标记，发现有没走过的点，就随意挑一个往前走，走不 了就回退，此种路径搜索策略就称为“深度优先搜索”，简称“深搜”。

其实称为“远度优先搜索”更容易理解些。因为这种策略能往前走一步就往前走一 步，总是试图走得更远。所谓远近(或深度），就是以距离起点的步数来衡量的。

代码框架

void dfs(当前状态)
{
	if(达到目标状态) 
	{
		...
		return;	
	}
	for(遍历下一层状态)
	{
		...
		dfs(下一层状态);
		...
	}
}

几个概念

• 状态：对问题在某一时刻的进展情况的数学描述（如迷宫题中当前所在位置）
• 状态转移：从一个状态扩展出(走出)其他状态的过程
• 剪枝：去掉搜索树中不需要的状态和转移
• 判重：已经搜索过的状态不再进行搜索
• 搜索树：由若干状态和状态转移形成的树形结构

问题引入：

给出一个矩阵，1表示墙壁不能走，0表示可以走，找出一条从左上角到右下角的最短路。

以递归的方式寻找路径，走不通就返回上一层。

1. 怎么找？一个点一个点地走。
2. 怎么判重？染色。
3. 怎么找最短？到达终点时更新答案
4. 终止条件？无路可走，到达终点

解决过程如图所示：

实现代码如下：

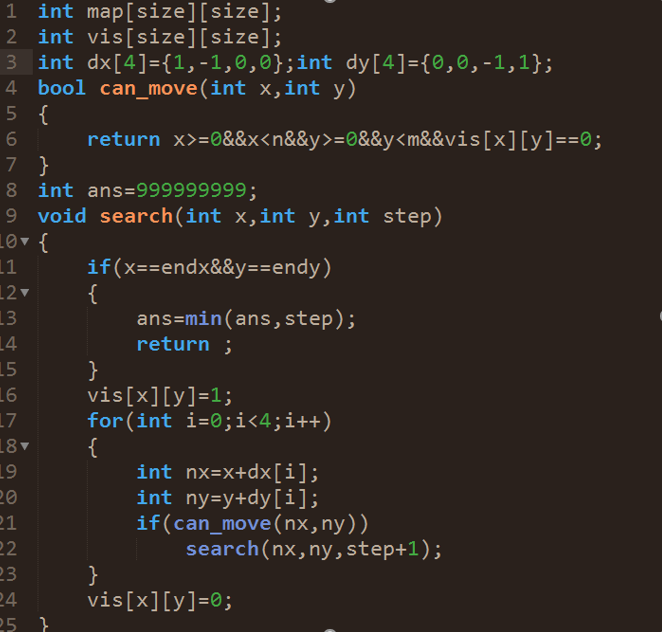
使用这种方法能解决问题：

时间复杂度：

每个状态最多有3种扩展方式，迷宫的最大深度为nm，因此时间复杂度可能达到O(3^(nm))

空间复杂度：

只需要记录每个节点是否被走过为O(n*m)

不过其实可以优化，这里就是接下来需要谈到的DFS剪枝

DFS剪枝

可以在下图中看到：

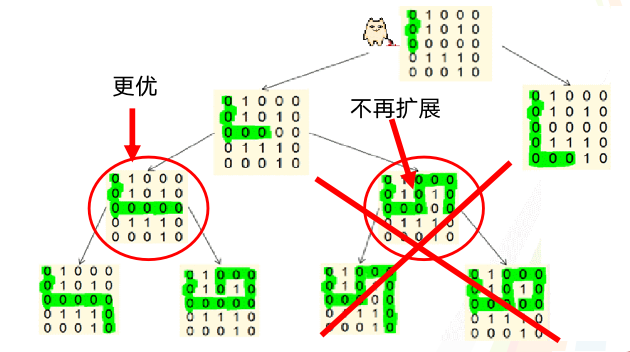
时间复杂度：

考虑搜索树，因为不会重复经过结点，所以深度不会超过n*m。 因此，每个结点最多只会遍历n*m次。 所以，时间复杂度最多可能达到O( (n*m)^2 )

空间复杂度：

只需要记录到达每个节点的最小步数
复杂度为O(n*m)

实现代码：

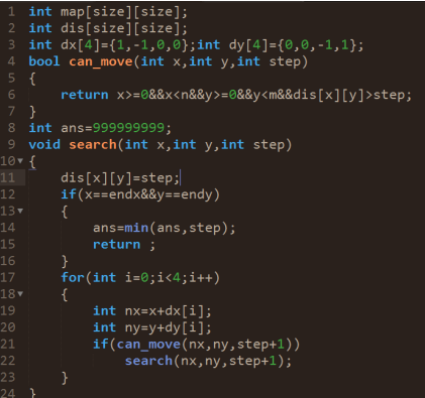
我们再用一个例子谈谈 DFS剪枝：

给出n个正整数a1,a2,a3,...,an，和一个正整数k, 问是否能从n个数中选出若干个数，使其和为k。

思路 ：

每个数只有选或不选两种选择：

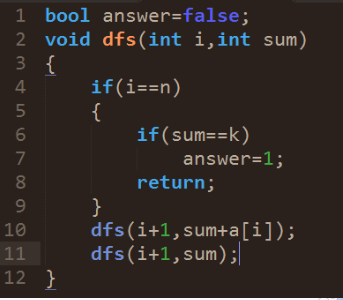
剪枝1：当sum>k时，直接返回

剪枝2：设s[i]表示第i个数到最后一个数的所有数和
当遍历到第i个数时，若此时sum加上所有剩下
的数也达不到k，即sum+s[i]<k，直接返回

DFS暂时先讲到这里，希望你有所收获。