八、广度优先搜索算法
广度优先搜索
广度优先搜索的过程
广度优先搜索算法(又称宽度优先搜索)是最简便的图的搜索算法之一,这一算法也是很多重要的图的算法的原型。
Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。
广度优先算法的核心思想是:从初始节点开始,应用算符生成第一层节点,检查目标节点是否在这些后继节点中,若没有,再用产生式规则将所有第一层的节点逐一扩展,得到第二层节点,并逐一检查第二层节点中是否包含目标节点。若没有,再用算符逐一扩展第二层的所有节点……,如此依次扩展,检查下去,直到发现目标节点为止。即
- 从图中的某一顶点V0开始,先访问V0;
- 访问所有与V0相邻接的顶点V1,V2,......,Vt;
- 依次访问与V1,V2,......,Vt相邻接的所有未曾访问过的顶点;
- 循此以往,直至所有的顶点都被访问过为止。
这种搜索的次序体现沿层次向横向扩展的趋势,所以称之为广度优先搜索。
广度优先搜索算法描述:
int Bfs()
{
初始化,初始状态存入队列;
队列首指针head=0; 尾指针tail=1;
do
{
指针head后移一位,指向待扩展结点;
for (int i=1;i<=max;++i) //max为产生子结点的规则数
{
if (子结点符合条件)
{
tail指针增1,把新结点存入列尾;
if (新结点与原已产生结点重复) 删去该结点(取消入队,tail减1);
else
if (新结点是目标结点) 输出并退出;
}
}
}while(head<tail); //队列为空
}
广度优先搜索注意事项:
1、每生成一个子结点,就要提供指向它们父亲结点的指针。当解出现时候,通过逆向跟踪,找到从根结点到目标结点的一条路径。当然不要求输出路径,就没必要记父亲。
2、生成的结点要与前面所有已经产生结点比较,以免出现重复结点,浪费时间和空间,还有可能陷入死循环。
3、如果目标结点的深度与“费用”(如:路径长度)成正比,那么,找到的第一个解即为最优解,这时,搜索速度比深度搜索要快些,在求最优解时往往采用广度优先搜索;如果结点的“费用”不与深度成正比时,第一次找到的解不一定是最优解。
4、广度优先搜索的效率还有赖于目标结点所在位置情况,如果目标结点深度处于较深层时,需搜索的结点数基本上以指数增长。
例题讲解
【例1】图4表示的是从城市A到城市H的交通图。从图中可以看出,从城市A到城市H要经过若干个城市。现要找出一条经过城市最少的一条路线。

【算法分析】
看到这图很容易想到用邻接距阵来表示,0表示能走,1表示不能走。如图。
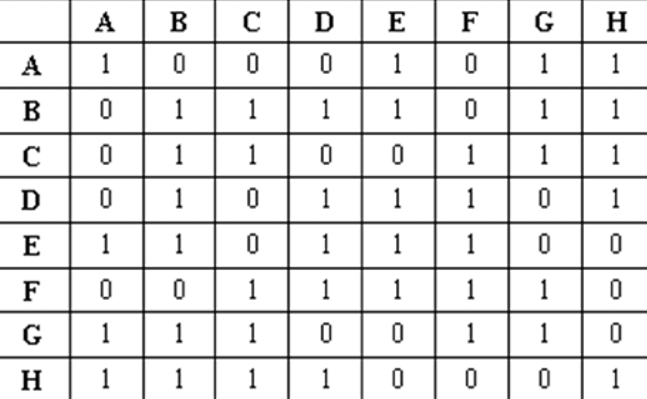
首先想到的是用队列的思想。a数组是存储扩展结点的队列,a[i]记录经过的城市,b[i]记录前趋城市,这样就可以倒推出最短线路。具体过程如下:
-
将城市A入队,队首为0、队尾为1。
-
将队首所指的城市所有可直通的城市入队(如果这个城市在队列中出现过就不入队,可用一布尔数组s[i]来判断),将入队城市的前趋城市保存在b[i]中。然后将队首加1,得到新的队首城市。重复以上步骤,直到搜到城市H时,搜索结束。利用b[i]可倒推出最少城市线路。
#include<iostream>
#include<cstring>
using namespace std;
int ju[9][9]={{0,0,0,0,0,0,0,0,0},
{0,1,0,0,0,1,0,1,1},
{0,0,1,1,1,1,0,1,1},
{0,0,1,1,0,0,1,1,1},
{0,0,1,0,1,1,1,0,1},
{0,1,1,0,1,1,1,0,0},
{0,0,0,1,1,1,1,1,0},
{0,1,1,1,0,0,1,1,0},
{0,1,1,1,1,0,0,0,1}};
int a[101],b[101];
bool s[9]; //初始化
int out(int d) //输出过程
{
cout<<char(a[d]+64);
while (b[d])
{
d=b[d];
cout<<"--"<<char(a[d]+64);
}
cout<<endl;
}
void doit()
{
int head,tail,i;
head=0;tail=1; //队首为0、队尾为1
a[1]=1; //记录经过的城市
b[1]=0; //记录前趋城市
s[1]=1; //表示该城市已经到过
do //步骤2
{
head++; //队首加一,出队
for (i=1;i<=8;i++) //搜索可直通的城市
if ((ju[a[head]][i]==0)&&(s[i]==0)) //判断城市是否走过
{
tail++; //队尾加一,入队
a[tail]=i;
b[tail]=head;
s[i]=1;
if (i==8)
{
out(tail);head=tail;break; //第一次搜到H城市时路线最短
}
}
}while (head<tail);
}
int main() //主程序
{
memset(s,false,sizeof(s));
doit(); //进行Bfs操作
return 0;
}
【例2】一矩形阵列由数字0到9组成,数字1到9代表细胞,细胞的定义为沿细胞数字上下左右还是细胞数字则为同一细胞,求给定矩形阵列的细胞个数。如:
阵列
4 10
0234500067
1034560500
2045600671
0000000089
有4个细胞。
【算法分析】
-
从文件中读入m*n矩阵阵列,将其转换为boolean矩阵存入bz数组中;
-
沿bz数组矩阵从上到下,从左到右,找到遇到的第一个细胞;
-
将细胞的位置入队h,并沿其上、下、左、右四个方向上的细胞位置入队,入队后的位置bz数组置为flase;
-
将h队的队头出队,沿其上、下、左、右四个方向上的细胞位置入队,入队后的位置bz数组置为flase;
-
重复4,直至h队空为止,则此时找出了一个细胞;
-
重复2,直至矩阵找不到细胞;
-
输出找到的细胞数。
#include<cstdio>
using namespace std;
int dx[4]={-1,0,1,0},
dy[4]={0,1,0,-1};
int bz[100][100],num=0,n,m;
void doit(int p,int q)
{
int x,y,t,w,i;
int h[1000][10];
num++;bz[p][q]=0;
t=0;w=1;h[1][1]=p;h[1][2]=q; //遇到的第一个细胞入队
do
{
t++; //队头指针加1
for (i=0;i<=3;i++) //沿细胞的上下左右四个方向搜索细胞
{
x=h[t][1]+dx[i];y=h[t][2]+dy[i];
if ((x>=0)&&(x<m)&&(y>=0)&&(y<n)&&(bz[x][y])) //判断该点是否可以入队
{
w++;
h[w][1]=x;
h[w][2]=y;
bz[x][y]=0;
} //本方向搜索到细胞就入队
}
}while (t<w); //直至队空为止
}
int main()
{
int i,j;
char s[100],ch;
scanf("%d%d\n",&m,&n);
for (i=0; i<=m-1;i++ )
for (j=0;j<=n-1;j++ )
bz[i][j]=1; //初始化
for (i=0;i<=m-1;i++)
{
gets(s);
for (j=0;j<=n-1;j++)
if (s[j]=='0') bz[i][j]=0;
}
for (i=0;i<=m-1;i++)
for (j=0;j<=n-1;j++)
if (bz[i][j])
doit(i,j); //在矩阵中寻找细胞
printf("NUMBER of cells=%d",num);
return 0;
}
【例3】最短路径(1995年高中组第4 题)
如下图所示,从入口(1)到出口(17)的可行路线图中,数字标号表示关卡。

现将上面的路线图,按记录结构存储如下图6:

请设计一种能从存储数据中求出从入口到出口经过最少关卡路径的算法。
【算法分析】
该题是一个路径搜索问题,根据图示,从入口(1)到出口(17)可能有多条途径,其中最短的路径只有一条,那么如何找最短路径呢?
根据题意,用数组NO存储各关卡号,用数组PRE存储访问到某关卡号的前趋关卡号。其实本题是一个典型的图的遍历问题,我们可以采用图的广度优先遍历,并利用队列的方式存储顶点之间的联系。
从入口(1)开始先把它入队,然后把(1)的所有关联顶点都入队,即访问一个顶点,将其后继顶点入队,并存储它的前趋顶点,……,直到访问到出口(17)。
最后,再从出口的关卡号(17)开始回访它的前趋关卡号,……,直到入口的关卡号(1),则回访的搜索路径便是最短路径。从列表中可以看出出口关卡号(17)的被访问路径最短的是:
(17)← (16)←(19)←(18)←(1)
由此,我们得到广度优先遍历求最短路径的基本方法如下:
假设用邻接矩阵存放路线图(a[I][j]=1表示I与j连通,a[I][j]=0表示I与j不连通)。 再设一个队列和一个表示拓展到哪个顶点的指针变量pos。
(1)从入口开始,先把(1)入队,并且根据邻接矩阵,把(1)的后继顶点全部入队,并存储这些后继顶点的前趋顶点为(1);再把pos后移一个,继续拓展它,将其后继顶点入队,并存储它们的前趋顶点,……,直到拓展到出口(目的地(17));
注意后继顶点入队前,必须要检查这个顶点是否已在队列中,如果已经在了就不要入队了;这一步可称为图的遍历或拓展;
(2)从队列的最后一个关卡号(出口(17))开始,依次回访它的前驱顶点,倒推所得到的路径即为最短路径。主要是依据每个顶点的前趋顶点倒推得到的。实现如下:
i=1 ;
WHILE (NO[I]!=17) ++i ;
DO
{
cout<<"("<<no[i]<<")";
cout<<" ←";
i=pre[i] ;
}
while ( I!=0);
【例4】迷宫问题
如下图所示,给出一个N*M的迷宫图和一个入口、一个出口。
编一个程序,打印一条从迷宫入口到出口的路径。这里黑色方块的单元表示走不通(用-1表示),白色方块的单元表示可以走(用0表示)。只能往上、下、左、右四个方向走。如果无路则输出“no way.”。

【算法分析】
只要输出一条路径即可,所以是一个经典的回溯算法问题,本例给出了回溯(深搜)程序和广搜程序。实现见参考程序。
【深搜参考程序】
#include <iostream>
using namespace std;
int n,m,desx,desy,soux,souy,totstep,a[51],b[51],map[51][51];
bool f;
int move(int x, int y,int step)
{
map[x][y]=step; //走一步,作标记,把步数记下来
a[step]=x; b[step]=y; //记路径
if ((x==desx)&&(y==desy))
{
f=1;
totstep=step;
}
else
{
if ((y!=m)&&(map[x][y+1]==0)) move(x,y+1,step+1); //向右
if ((!f)&&(x!=n)&&(map[x+1][y]==0)) move(x+1,y,step+1); //往下
if ((!f)&&(y!=1)&&(map[x][y-1]==0)) move(x,y-1,step+1); //往左
if ((!f)&&(x!=1)&&(map[x-1][y]==0)) move(x-1,y,step+1); //往上
}
}
int main()
{
int i,j;
cin>>n>>m; //n行m列的迷宫
for (i=1;i<=n;i++) //读入迷宫,0表示通,-1表示不通
for (j=1;j<=m;j++)
cin>>map[i][j];
cout<<"input the enter:";
cin>>soux>>souy; //入口
cout<<"input the exit:";
cin>>desx>>desy; //出口
f=0; //f=0表示无解;f=1表示找到了一个解
move(soux,souy,1);
if (f)
{
for (i=1;i<=totstep;i++) //输出直迷宫的路径
cout<<a[i]<<","<<b[i]<<endl;
}
else cout<<"no way."<<endl;
return 0;
}
【广搜参考程序】
#include <iostream>
using namespace std;
int u[5]={0,0,1,0,-1},
w[5]={0,1,0,-1,0};
int n,m,i,j,desx,desy,soux,souy,head,tail,x,y,a[51],b[51],pre[51],map[51][51];
bool f;
int print(int d)
{
if (pre[d]!=0) print (pre[d]); //递归输出路径
cout<<a[d]<<","<<b[d]<<endl;
}
int main()
{
int i,j;
cin>>n>>m; //n行m列的迷宫
for (i=1;i<=n;i++) //读入迷宫,0表示通,-1表示不通
for (j=1;j<=m;j++)
cin>>map[i][j];
cout<<"input the enter:";
cin>>soux>>souy; //入口
cout<<"input the exit:";
cin>>desx>>desy; //出口
head=0;
tail=1;
f=0;
map[soux][souy]=-1;
a[tail]=soux; b[tail]=souy; pre[tail]=0;
while (head!=tail) //队列不为空
{
head++;
for (i=1;i<=4;i++) //4个方向
{
x=a[head]+u[i]; y=b[head]+w[i];
if ((x>0)&&(x<=n)&&(y>0)&&(y<=m)&&(map[x][y]==0))
{ //本方向上可以走
tail++;
a[tail]=x; b[tail]=y; pre[tail]=head;
map[x][y]=-1;
if ((x==desx)&&(y==desy)) //扩展出的结点为目标结点
{
f=1;
print(tail);
break;
}
}
}
if (f) break;
}
if (!f) cout<<"no way."<<endl;
return 0;
}





