一、复杂度分析
复杂度理论
算法时间复杂度的数学意义
从数学上定义,给定算法A,如果存在函数f(n),当n=k时,f(k)表示算法A在输入规模为k的情况下的运行时间,则称f(n)为算法A的时间复杂度。
其中:输入规模是指算法A所接受输入的自然独立体的大小,我们总是假设算法的输入规模是用大于零的整数表示的,即n=1,2,3,……,k,……
对于同一个算法,每次执行的时间不仅取决于输入规模,还取决于输入的特性和具体的硬件环境在某次执行时的状态。所以想要得到一个统一精确的F(n)是不可能的。为此,通常做法:
1. 忽略硬件及环境因素,假设每次执行时硬件条件和环境条件是完全一致的。
2. 对于输入特性的差异,我们将从数学上进行精确分析并带入函数解析式。
例子:
x=1;
for(i=1;i<=n;i++)
for(j=1;j<=i;j++)
for(k=1;k<=j;k++)
x++;
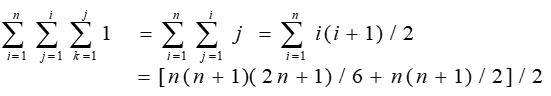
算法的渐近时间复杂度
很多时候,我们不需要进行如此精确的分析,究其原因:
1.在较复杂的算法中,进行精确分析是非常复杂的。
2.实际上,大多数时候我们并不关心F(n)的精确度量,而只是关心其量级。
算法复杂度的考察方法
(1)考察一个算法的复杂度,一般考察的是当问题复杂度n的增加时,运算所需时间、空间代价f(n)的上下界。
(2)进一步而言,又分为最好情况、平均情况、最坏情况三种情况。通常最坏情况往往是我们最关注的。
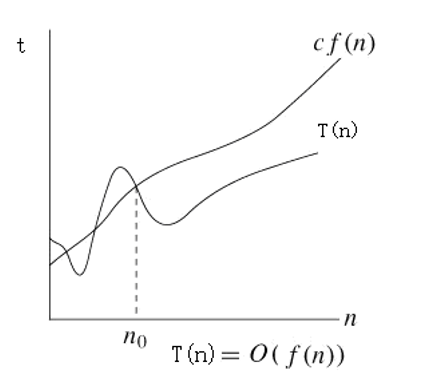
上界函数
定义1 如果存在两个正常数c和n0,对于所有的n≥n0,有
|T(n)| ≤ c|f(n)|
则记作T(n) = Ο(f(n))
含义:
-
如果算法用n值不变的同一类数据在某台机器上运行时,所用的时间总是小于|f(n)|的一个常数倍。所以f(n)是计算时间T(n)的一个上界函数。
-
试图求出最小的f(n),使得T(n) = Ο(f(n))。
在分析算法的时间复杂度时,我们更关心最坏情况而不是最好情况,理由如下:
-
最坏情况给出了算法执行时间的上界,我们可以确信,无论给什么输入,算法的执行时间都不会超过这个上界,这样为比较和分析提供了便利。
-
虽然最坏情况是一种悲观估计,但是对于很多问题,平均情况和最坏情况的时间复杂度差不多,比如插入排序这个例子,平均情况和最坏情况的时间复杂度都是输入长度n的二次函数。
下界函数
定义1.2 如果存在两个正常数c和n0,对于所有的n≥n0,有
|T(n)| ≥ c|g(n)|,则记作T(n) = Ω(g(n))
含义:
-
如果算法用n值不变的同一类数据在某台机器上运行时,所用的时间总是不小于|g(n)|的一个常数倍。所以g(n)是计算时间T(n)的一个下界函数。
-
试图求出“最大”的g(n),使得T(n) = Ω(g(n))。
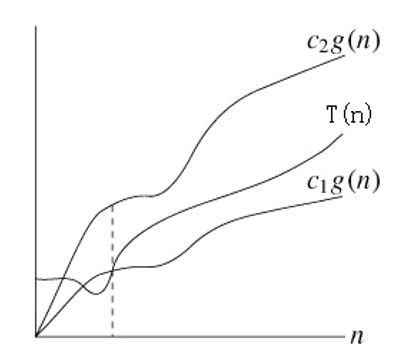
“平均情况”限界函数
定义1.3 如果存在正常数c1,c2和n0,对于所有的n≥n0,有
c1|g(n)| ≤|T(n)| ≤ c2|g(n)|
则记作
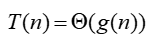
含义:
- 算法在最好和最坏情况下的计算时间就一个常数因子范围内而言是相同的。可看作:
既有 T(n) = Ω(g(n)),又有T(n) = Ο(g(n))
常见算法时间复杂度:
-
O(1): 表示算法的运行时间为常量
-
O(n): 表示该算法是线性算法
-
O(㏒2n): 二分搜索算法
-
O(n㏒2n): 快速排序算法
-
O(n^2): 对数组进行排序的各种简单算法,例如直接插入排序的算法。
-
O(n^3): 做两个n阶矩阵的乘法运算
-
O(2^n): 求具有n个元素集合的所有子集的算法
-
O(n!): 求具有N个元素的全排列的算法
优<---------------------------<劣
O(1)<O(㏒2n)<O(n)< O(n㏒2n): <O(n2)<O(2n)
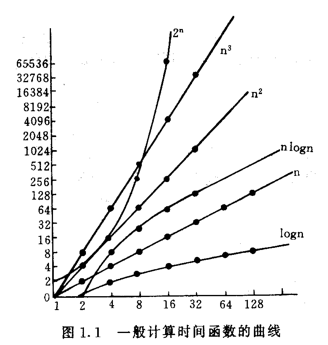
典型的计算时间函数曲线
计算算法时间复杂度过程:
- 确定基本操作
- 构造基于基本操作的函数解析式
- 求解函数解析式
- 如果构建的是递推关系式,那么常用的求解方法有:
(1)前向替换法
可以从初始条件给出的序列初始项开始,使用递推方程生成序列的前面若干项,寄希望于从中找出一个能够用闭合公式表示的模式。如果找到了这样的公式,我们可以用两种方法对它进行验证:第一,将它直接代入递归方程和初始条件中。第二,用数学归纳法来证明。
例如,考虑如下递推式
X(n) = 2X(n-1) +1 n>1
X(1) = 1
x(1)=1
x(2)=2x(1)+1 = 2*1+1=3
x(3)=2x(2)+1=2*3+1=7
x(4)=2x(3)+1=2*7+1=15
X(n)=2^n-1 n>0
(2)反向替换法
例如:X(n)=x(n-1)+n
使用所讨论的递推关系,将x(n-1)表示为x(n-2)得函数,然后把这个结果代入原始方程,来把x(n)表示为x(n-2)的函数。重复这一过程。
X(n)=x(0)+1+2+3+4+5…+n=0+1+2+3=4 = n(n+1)/2
(3)换名
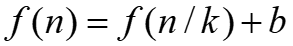
上面形式的在递推关系式,一个规模为n的问题,每一次递归调用后,都简化为n/k规模的问题,为了方便求解,我们通常设定:n=km,
则,上面的求解过程可简化为:
f(n)= f(km-1)+b
= f(km-2)+2b
= …
= f(k0)+mb
= f(1) + blog n
几种常见复杂度举例:
- O(logn):我们学过的算法,二分搜索
int BinSrch(Type A[],int i, int n, Type x)
//A[i..n]是非递减排列 且 1<=i<=n;
{
if(n==i) { if(x==A[i]) return i;
else return 0; }
else
{
int mid=(i+n)/2;
if(x==A[mid]) return mid; ----基本操作
else if(x<A[mid]) return BinSrh(A, i, mid-1, x);——递归调用
else if(x>A[mid]) return BinSrh(A, mid+1, n, x);——递归调用
}
}
递归关系式:
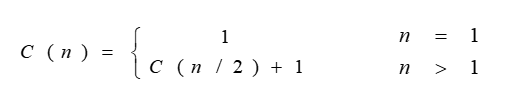
因为规模每一次递归调用后,缩减为原来的1/2,所以采用换名方法求解,设 n = 2k:
C(n) = C(2k)= C(2k-1)+1
= C(2k-2) + 2
=…
=C(2k-k)+k
=C(1) + k
= logn+1
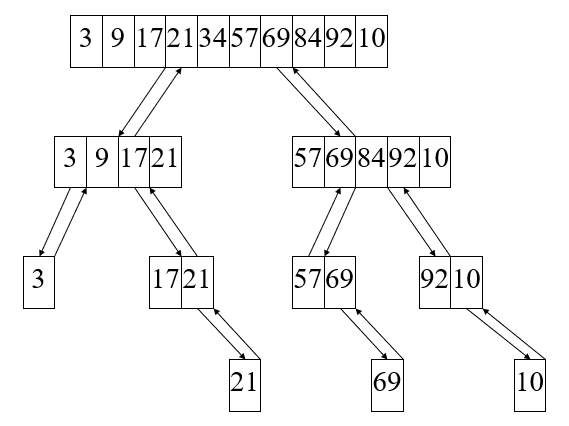
观察递归调用的过程以及递推关系式:
-
在递归关系式中:递归调用共有k次,我们设n= 2k,k=logn
-
递归调用的二叉树型结构中,调用次数为二叉树的深度。
- O(n): 表示该算法是线性算法
目前所学的算法中有:线性选择算法
int Select(int data[],int p,int r,int k)
{
if(p>r) return -1; //p不能大于r
if(p==r) return data[p]; //p<r
int s=partion(data,p,r); --------基本操作
if (s==k) return data[s];
else if(s>k)
{
int r1= Select(data,p,s-1,k);-----递归调用
return r1;
}
else //s<k
{
int r1=Select(data,s+1,r,k-s);-----递归调用
return r1;
}
}
如果递归调用,每次规模是原来的1/2:
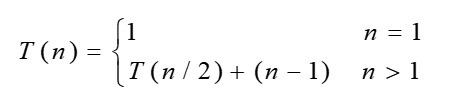
因为每一次规模都减到原来的1/2,所以用换名的方法设 n = 2k:
T(n) = T(n/2) + (n-1)
= T(2k-1) + (2k-1)
=[T(2k-2) + (2k-1-1)]+ (2k-1)
=…
=[T(2k-k) + (21-1)] + … +(2k-1-1) +(2k-1)
=T(1)+[(2k+1-2)-k]
=2n-logn-1
算法时间复杂度:O(n)
分析:
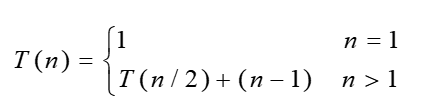
算法的复杂度有两部分决定:递归和合并。
递归的复杂度是:logn,合并的复杂度是 n。
3.O(nlogn)
所学过的算法:快速排序、堆排序等,分治法中的平面中最接近点对问题。
递推关系式:
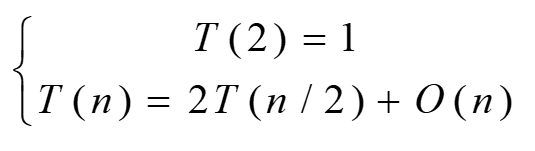
T(n)=2T(n/2) +n 设n= 2k
=2T(2k-1)+2k
=2[2T(2k-2)+2k-1]+2k
=22T(2k-2)+2*2k
=…
=2k-1T(2k-(k-1)) + (k-1)*2k
=n/2 + (logn-1) *n
不失一般性,设规模为n的问题,每一次有分解为m个子问题,设n =mk,则:
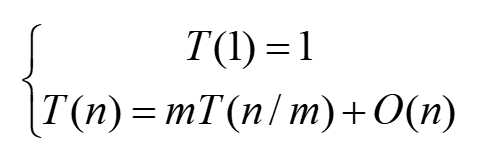
T(n)=mT(n/m) +n
=mT(mk-1)+mk
=m[mT(mk-2)+mk-1]+mk
=m2T(mk-2)+2*mk
=…
=mkT(2k-k) + k*mk
=n + logn *n
算法时间复杂度:O(nlogn)
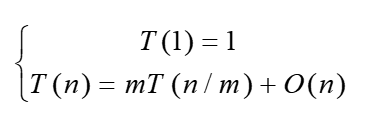
分析:
算法的复杂度有两部分决定:递归和合并,递归的复杂度是:n,合并的复杂度是 nlogn。
- O(n^2)
通常的两层嵌套循环,内层的运算执行次数,学过的例子有:比赛日程
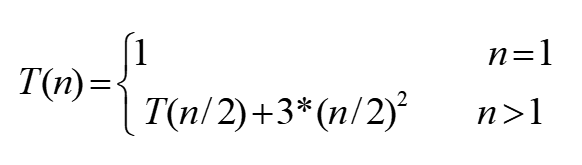
T(n)=T(n/m)+(n/m)2 设n=mk
=T(mk-1)+m2(k-1)
=[T(mk-2)+m2(k-2) ]+ m2(k-1)
=…
=[T(mk-k)+m0]+… + m2(k-2)+m2(k-1)
=1+(m2k-1)/(m2-1)
=(n2-1)/(m2-1)+1
所以:O(n2)
- O(n^k)
所学过的:大整数乘法
Recursive_Miltiply(x,y)
{
if n=1
if (X=1)and(Y=1) return(1)
else return(0)
x1 =X的左边n/2位;
x0 =X的右边n/2位;
y1 =Y的左边n/2位;
y0 =Y的右边n/2位;
p = Recursive_Miltiply(x1+x0,y1+y0);——递归调用
x1y1 = Recursive_Miltiply(x1,y1);——递归调用
x0y0 = Recursive_Miltiply(x0,y0);——递归调用
return x1y1*2n + (p-x1y1-x0y0)*2n/2+x0y0;——基本操作
}
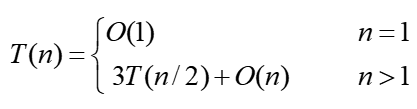
设,n=2k, 用反向替换法对它求解:
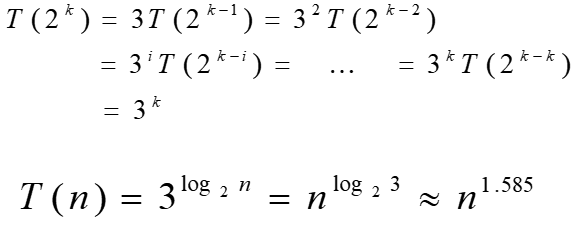
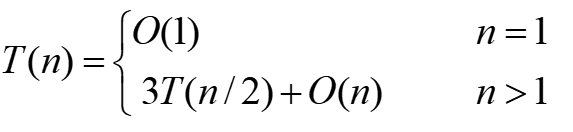
分析:
在这个递推关系式中,算法每次递归调用3个规模为1/2的子问题,那么总的规模3/2,大小,所以,粗略估算要在O(nlogn)、O(n2)之间。




