JAVA深度优先和广度优先遍历

深度优先和广度优先遍历，概念性的问题不想讲太多，毕竟网上有专门的，主要讲讲思路

接下来对这颗树进行深度、广度遍历

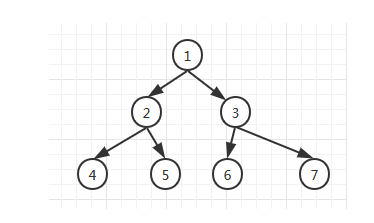
深度优先遍历：深度优先遍历是图论中的经典算法。其利用了深度优先搜索算法可以产生目标图的相应拓扑排序表，采用拓扑排序表可以解决很多相关的图论问题，如最大路径问题等等。

根据深度优先遍历的特点我们利用Java集合类的栈Stack先进后出的特点来实现。我用二叉树来进行深度优先搜索。

深度优先搜索的步骤为：（这儿需要借助栈来完成节点访问操作）

（1）、首先节点 1 进栈，节点1在栈顶；

（2）、然后节点1出栈，访问节点1，节点1的孩子节点3进栈，节点2进栈；

（3）、节点2在栈顶，然后节点2出栈，访问节点2

（4）、节点2的孩子节点5进栈，节点4进栈

（5）、节点4在栈顶，节点4出栈，访问节点4，

（6）、节点4左右孩子为空，然后节点5在栈顶，节点5出栈，访问节点5；

（7）、节点5左右孩子为空，然后节点3在站顶，节点3出栈，访问节点3；

（8）、节点3的孩子节点7进栈，节点6进栈

（9）、节点6在栈顶，节点6出栈，访问节点6；

（10）、节点6的孩子为空，这个时候节点7在栈顶，节点7出栈，访问节点7

（11）、节点7的左右孩子为空，此时栈为空，遍历结束。

 

广度优先遍历：广度优先遍历是连通图的一种遍历策略，因为它的思想是从一个顶点V0开始，辐射状地优先遍历其周围较广的区域故得名。

根据广度优先遍历的特点我们利用Java数据结构队列Queue来实现。

广度优先搜索的步骤为：（这儿需要借助队列来完成节点访问操作）

（1）、节点1进队，节点1出队，访问节点1

（2）、节点1的孩子节点2进队，节点3进队。

（3）、节点2出队，访问节点2，节点2的孩子节点4进队，节点5进队；

（4）、节点3出队，访问节点3，节点3的孩子节点6进队，节点7进队；

（5）、节点4出队，访问节点4，节点4没有孩子节点。

（6）、节点5出队，访问节点5，节点5没有孩子节点。

（7）、节点6出队，访问节点6，节点6没有孩子节点。

（8）、节点7出队，访问节点7，节点7没有孩子节点，结束。

实现：

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

/**
 * 树的深度优先和广度优先搜索
 */
public class TreeSearch {

    /**
     *                  head:1
     *                     /\
     *                   /   \
     *            second:2   three:3
     *             /\            /\
     *           /   \         /   \
     *      four:4   five:5  six:6  seven:7
     * @param args
     */
    public static void main(String[] args) {
        TreeNode head=new TreeNode(1);
        TreeNode second=new TreeNode(2);
        TreeNode three=new TreeNode(3);
        TreeNode four=new TreeNode(4);
        TreeNode five=new TreeNode(5);
        TreeNode six=new TreeNode(6);
        TreeNode seven=new TreeNode(7);
        head.rightNode=three;
        head.leftNode=second;
        second.rightNode=five;
        second.leftNode=four;
        three.rightNode=seven;
        three.leftNode=six;
        System.out.print("广度优先遍历结果：");
        new TreeSearch().BroadFirstSearch(head);
        System.out.println();
        System.out.print("深度优先遍历结果：");
        new TreeSearch().depthFirstSearch(head);
    }

    //广度优先遍历是使用队列实现的
    public void BroadFirstSearch(TreeNode nodeHead) {
        if(nodeHead==null) {
            return;
        }
        Queue<TreeNode> myQueue=new LinkedList<>();
        myQueue.add(nodeHead);
        while(!myQueue.isEmpty()) {
            TreeNode node=myQueue.poll();
            System.out.print(node.data+" ");
            if(null!=node.leftNode) {
                myQueue.add(node.leftNode);    //深度优先遍历，我们在这里采用每一行从左到右遍历
            }
            if(null!=node.rightNode) {
                myQueue.add(node.rightNode);
            }

        }
    }

    //深度优先遍历
    public void depthFirstSearch(TreeNode nodeHead) {
        if(nodeHead==null) {
            return;
        }
        Stack<TreeNode> myStack=new Stack<>();
        myStack.add(nodeHead);
        while(!myStack.isEmpty()) {
            TreeNode node=myStack.pop();    //弹出栈顶元素
            System.out.print(node.data+" ");
            if(node.rightNode!=null) {
                myStack.push(node.rightNode);    //深度优先遍历，先遍历左边，后遍历右边,栈先进后出
            }
            if(node.leftNode!=null) {
                myStack.push(node.leftNode);
            }
        }

    }

}

// 节点结构
class TreeNode {
    int data;
    TreeNode leftNode;
    TreeNode rightNode;
    public TreeNode() {
    }
    public TreeNode(int d) {
        data=d;
    }
    public TreeNode(TreeNode left,TreeNode right,int d) {
        leftNode=left;
        rightNode=right;
        data=d;
    }
}